Кинематические уравнения для кватернионов

⇐ ПредыдущаяСтр 5 из 5

Для получения дифференциального уравнения для кватерниона, соответствующего вектору конечного поворота, воспользуемся решением рассмотренной выше задачи о движении базиса относительно базиса . В моменты времени t ₁₂ и t ₁₃ подвижный базис занимает положения 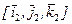и соответственно, причем ориентация базиса 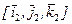относительно определяется кватернионом

а базиса относительно – кватернионом

Угловое положение базиса относительно базиса 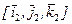определяется кватернионом

Здесь о², о³ и о⁴ – малые величины порядка малости выше второго, третьего и четвертого соответственно.

При построении этих кватернионов использовалась формула (7.26). Для получения выражения для производной кватерниона воспользуемся определением производной как предела и, учитывая очевидное равенство

, получим:

Вычислив этот предел с учетом выражения (7.33) для скорости , получим (при этом учтем также, что кватернион соответствует произвольно взятому моменту времени t ₁₂ и при записи окончательного выражения для производной может быть заменен на более общее обозначение – Q):

. (7.52)

Отметим, что формула (7.52) получена для кватерниона Q поворота от базиса к базису 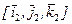, обратному повороту соответствует сопряженный кватернион Q *. Кинематическое уравнение для сопряженного кватерниона получим, осуществив процедуру инвертирования для правой и левой частей уравнения (7.52):

. (7.53)

Отметим также, что в обеих формулах (7.52) и (7.53) вектор – это вектор угловой скорости базиса 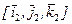относительно базиса , спроецированный на оси базиса 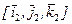. Можно переписать эти формулы для случая, когда вектор спроецирован на оси базиса в соответствии с (7.31).

Обобщим эти результаты для любых двух трехгранников Ob ₁ b ₂ b ₃ и Oe ₁ e ₂ e ₃, условно обозначенных Beg и End. Пусть поворот от «начального» (Beg) к «конечному» (End) трехгранникам описывается кватернионом Q , обратный поворот – сопряженным кватернионом Q *. Пусть трехгранник Oe ₁ e ₂ e ₃ относительно трехгранника Ob ₁ b ₂ b ₃ вращается с угловой скоростью , а трехгранник Ob ₁ b ₂ b ₃ относительно Oe ₁ e ₂ e ₃ – с угловой скоростью = – . Разложение вектора по базису трехгранника Ob ₁ b ₂ b ₃ имеет вид:

а по базису трехгранника Oe ₁ e ₂ e ₃ – вид:

соответственно, разложение вектора по базису трехгранника Ob ₁ b ₂ b ₃ имеет вид:

а по базису трехгранника Oe ₁ e ₂ e ₃ – вид:

Тогда кинематические уравнения (7.52) и (7.53) принимают вид:

(7.54а)

(7.54б)

Все уравнения (7.54) эквиваленты и при решении практических задач можно выбирать любые, предпочтение следует отдавать тем, которые содержат доступные скалярные составляющие векторов и . В качестве примера запишем дифференциальные уравнения для введенных ранее кватернионов:

· для кватерниона вращения от ОХ_и Y _и Z _и к ОХ YZ с угловой скоростью :