Связь вектора конечного поворота и кватернионов с направляющими косинусами
Для совмещения векторных базисов двух координатных трехгранников можно использовать один поворот на фиксированный угол θ вокруг оси, которая называется осью Эйлера и положение которой в пространстве определяется единичным вектором 
. Всю эту информацию предоставляет вектор конечного поворота:
, (7.6)
где 
– проекции единичного вектора на базисные векторы 
.
Для получения выражений, связывающих параметры вектора конечного поворота с направляющими косинусами, рассмотрим задачу поворота произвольного вектора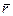 
вокруг вектора конечного поворота 
на угол θ, обозначив через 
результирующий вектор.
1. Разложим вектор 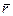по базису ( , 
), т.е. представим в виде суммы двух векторов по заданному базису (рис. 7.11):
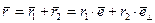, (7.7)
где: 
; - единичный вектор, перпендикулярный вектору .
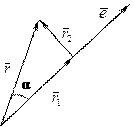
Рис. 7.11. Разложение исходного вектора по базису
Представим скалярную величину r 1 в виде скалярного произведения векторов:
,
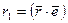а вектор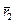 
как двойное векторное произведение:
,
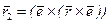причем легко видеть, что 
. Таким образом, выражения (7.7) запишется в следующем виде:
. (7.8)
|
|
|
Примечание. Скалярное произведение двух векторов 
есть скаляр 
, где g -угол между векторами. Векторное произведение двух векторов есть вектор, модуль которого равен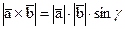 
. Основные свойства векторного произведения: 
.
2. Осуществим поворот вектора 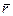вокруг вектора на угол θ. Очевидно, что при таком повороте (рис. 7.11) составляющая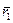 
не изменится, а составляющая 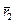повернется в плоскости, перпендикулярной вектору , на угол θ. Обозначим этот повернутый вектор как 
, тогда:
. (7.9)
Для получения выражений для вектора рассмотрим плоскость, перпендикулярную , в которой осуществляется поворот 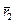, и представим координатный базис этой плоскости в виде двух взаимно-перпендикулярных векторов, перпендикулярных также вектору . Такими векторами являются векторы 
и 
(рис. 7.12). Модули этих векторов равны между собой и равны 
.
Таким образом, искомый вектор можно представить в следующем виде (рис. 7.12):
. (7.10)
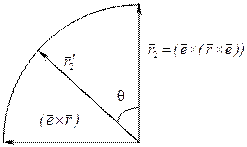
Рис.7.12. Разложение повернутого вектора по базису
3. Подставляя полученное выражение (7.10) в (7.9), найдем искомый вектор :
.
|
|
|
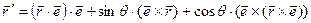Заменим первое слагаемое правой части этой формулы на выражение, полученное из (7.8)
,
получим
,
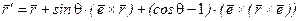или
,
или, окончательно
. (7.11)
Используя (7.11), получим искомые выражения, связывающие параметры вектора конечного поворота с направляющими косинусами. Рассмотрим две системы координат: первая из них имеет базис 
, вторая – базис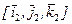 
. Ортогональное преобразование (поворот) первой системы координат во вторую запишем в векторно-матричном формализме через матрицу направляющих косинусов:
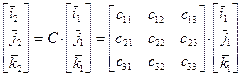, (7.12)
где С – соответствующая матрица направляющих косинусов.
Осуществим также поворот базиса первой системы координат в базис второй системы координат 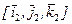с помощью вектора конечного поворота . Отметим очевидный факт, что проекции вектора конечного поворота одинаковы в обеих системах координат, поэтому проекции вектора в обеих системах координат будем обозначать как:
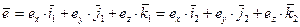. (7.13)
Осуществим поворот трех векторов 
вокруг вектора конечного поворота 
на угол θ, в результате получим соответственно вектора 
. Связь этих векторов описывается выражениями (7.11):
|
|
|
,
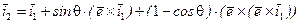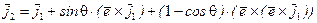, (7.14)
.
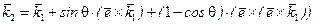Преобразуем первое из выражений (7.25):
,
.
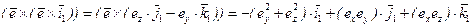После подстановки в первое выражение (7.14) и группировки слагаемых имеем:
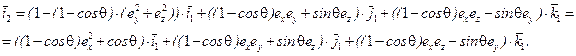(7.15)
Преобразуем второе из выражений (7.14):
,
.
После подстановки во второе выражение (7.25) и группировки слагаемых имеем:
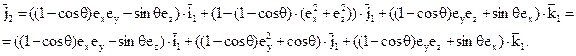(7.16)
Преобразуем третье из выражений (7.14):
,
.
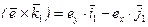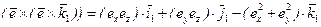После подстановки во второе выражение (7.14) и группировки слагаемых имеем:
(7.17)
Запишем выражение (7.12) с учетом (7.15),(7.16),(7.17):
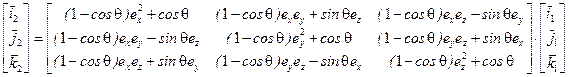. (7.18)
Сопоставляя (7.12) и (7.18), получим выражения для элементов матрицы направляющих косинусов через параметры вектора конечного поворота:
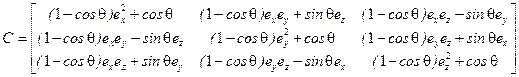. (7.19)
С помощью выражений (7.19) можно решить обратную задачу: выразить параметры вектора конечного поворота через элементы матрицы направляющих косинусов. Сумма элементов, стоящих на главной диагонали, равна: 
, откуда:
. (7.20)
Разность элементов матрицы направляющих косинусов, стоящих симметрично от главной диагонали, даст выражения проекций единичного вектора:
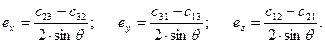(7.21)
|
|
|
Полученные выражения (7.19)÷(7.21), связывающие параметры вектора конечного поворота с элементами матрицы направляющих косинусов, справедливы для всех таблиц 7.1÷7.16. Это очень важное замечание служит основой для построения алгоритмов обработки информации, использующих векторы конечных поворотов.
С вектором конечного поворота непосредственно связаны параметры Родрига-Гамильтона, которые для вектора, заданного в виде (7.6), определяются так:
; 
; 
; 
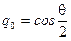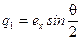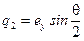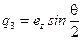, (7.22)
удовлетворяя при этом условию нормировки:
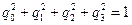. (7.23)
Для обеспечения компактности математических преобразований четверка параметров Родрига-Гамильтона записывается в виде гиперкомплексного числа – нормированного кватерниона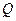 
, определяемого как
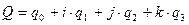. (7.24)
Здесь i , j , k – мнимые единицы, различающиеся между собой и удовлетворяющие условиям:
; 
; 
;
; 
; 
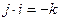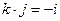; (7.25)
; 
; 
.
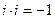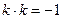Кватернион 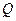, соответствующий вектору конечного поворота 
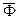, заданному в виде (7.6), может быть записан как
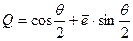, (7.26)
при этом базисные векторы формально заменяются на мнимые единицы i , j , k. Кватернион определяет ось вращения и угол поворота.
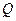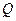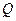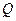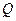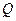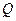Поворот от одного координатного трехгранника к другому описывается соответствующим кватернионом. Умножение кватернионов 1 и 2 даёт такой результирующее вращение, как если бы объект сначала повернули на 1, а затем на 2. При этом 1× 2 ¹ 2× 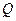1. Сложение кватернионов даёт вращение, находящееся между этими двумя кватернионами. Из (7.19) и (7.22) можно получить выражения, связывающие параметры Родрига-Гамильтона с элементами соответствующей матрицы направляющих косинусов. Для этого воспользуемся формулами тригонометрии для двойных углов
, 
, 
,
подставив которые в (7.19), нетрудно заметить, что, например, элемент матрицы С, лежащий на пересечении первой строки и первого столбца, запишется в виде
,
а на пересечении второй строки и первого столбца – в виде
.
Общий вид матрицы С при этом будет следующим:
. (7.27)
Обратные соотношения, выражающие параметры Родрига-Гамильтона через элементы матрицы направляющих косинусов, получим из (7.20) и (7.21) с учетом тех же формул тригонометрии. Так, из (7.20) следует
,
а из (7.22) следует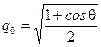 
, откуда непосредственно вытекает вид формулы для q0. Используя эту формулу, из (7.21) несложно выразить параметры q1, q2, q3. Окончательно получим:
; (7.28)
; 
; 
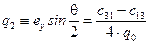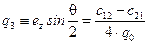. (7.29)
Отметим, что подкоренное выражение в формуле (7.28) всегда неотрицательное, поэтому имеет смысл для любых вариантов взаимной ориентации двух трехгранников. При этом всегда q0 ≥ 0, что соответствует диапазону значений угла θ от–π до π включительно. При θ = ±π величина q0 = 0 и выражения (7.29) не определены. В этом случае параметры q1, q2, q3 можно выразить из диагональных элементов матрицы С, записанной в виде (7.27):
; 
; 
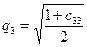. (7.30)
Дата добавления: 2021-01-21; просмотров: 362; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!