Индивидуальные задания для контрольной работы.
Задача № 1. Вычислить неопределенный интеграл методом непосредственного интегрирования.
1.1. 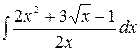 .
.
1.2. 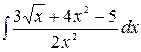 .
.
1.3. 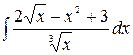 .
.
1.4. 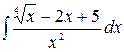 .
.
1.5. 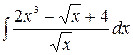 .
.
1.6. 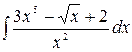 .
.
1.7. 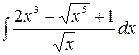 .
.
1.8. 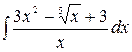 .
.
1.9. 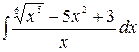 .
.
1.10. 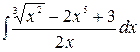 .
.
1.11. 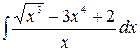 .
.
1.12. 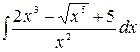 .
.
1.13. 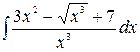 .
.
1.14. 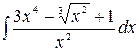 .
.
1.15. 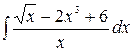 .
.
1.16. 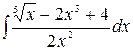 .
.
1.17. 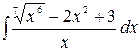 .
.
1.18. 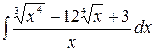 .
.
1.19. 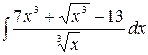 .
.
1.20. 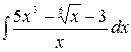 .
.
1.21. 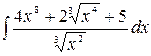 .
.
1.22. 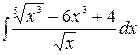 .
.
1.23. 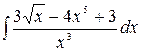 .
.
1.24. 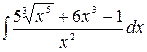 .
.
1.25. 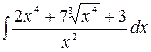 .
.
1.26. 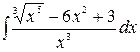 .
.
1.27. 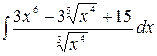 .
.
1.28. 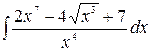 .
.
1.29. 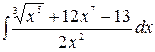 .
.
1.30. 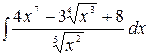 .
.
Задача № 2. Вычислить неопределенный интеграл методом непосредственного интегрирования.
2.1. 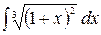 .
.
2.2. 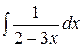 .
.
2.3. 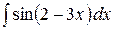 .
.
2.4. 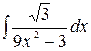 .
.
2.5. 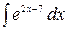 .
.
2.6. 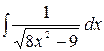 .
.
2.7. 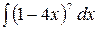 .
.
2.8. 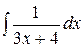 .
.
2.9. 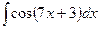 .
.
2.10. 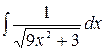 .
.
2.11. 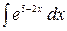 .
.
2.12. 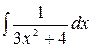 .
.
2.13. 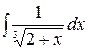 .
.
2.14. 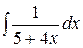 .
.
2.15. 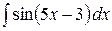 .
.
2.16. 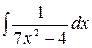 .
.
2.17. 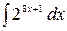 .
.
2.18. 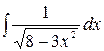 .
.
2.19. 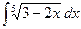 .
.
2.20. 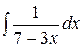 .
.
2.21. 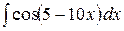 .
.
2.22. 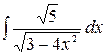 .
.
2.23. 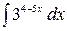 .
.
2.24. 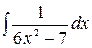 .
.
2.25. 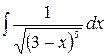 .
.
2.26. 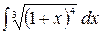 .
.
2.27. 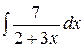 .
.
2.28. 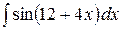 .
.
2.29. 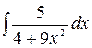 .
.
2.30. 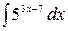 .
.
Задача № 3. Вычислить неопределенный интеграл методом замены переменной.
3.1. 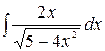 .
.
3.2. 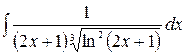 .
.
3.3. 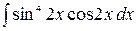 .
.
3.4. 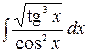 .
.
3.5. 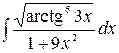 .
.
3.6. 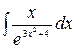 .
.
3.7. 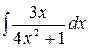 .
.
3.8. 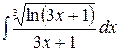 .
.
3.9. 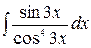 .
.
3.10. 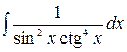 .
.
3.11. 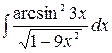 .
.
3.12. 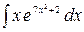 .
.
3.13. 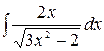 .
.
3.14. 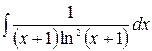 .
.
3.15. 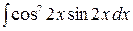 .
.
3.16. 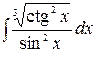 .
.
3.17. 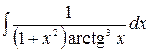 .
.
3.18. 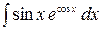 .
.
3.19. 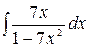 .
.
3.20. 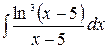 .
.
3.21. 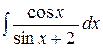 .
.
3.22. 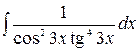 .
.
3.23. 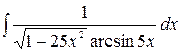 .
.
3.24. 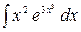 .
.
3.25. 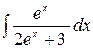 .
.
3.26. 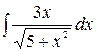 .
.
3.27. 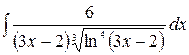 .
.
3.28. 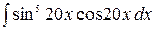 .
.
3.29. 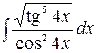 .
.
3.30. 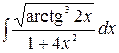 .
.
Задача № 4. Вычислить неопределенный интеграл методом замены переменной.
4.1. 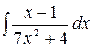 .
.
4.2. 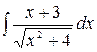 .
.
4.3. 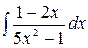 .
.
4.4. 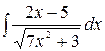 .
.
4.5. 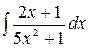 .
.
4.6. 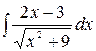 .
.
4.7. 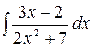 .
.
4.8. 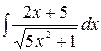 .
.
4.9. 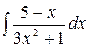 .
.
4.10. 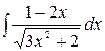 .
.
4.11. 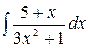 .
.
4.12. 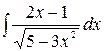 .
.
4.13. 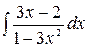 .
.
4.14. 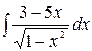 .
.
4.15. 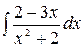 .
.
4.16. 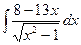 .
.
4.17. 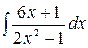 .
.
4.18. 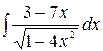 .
.
4.19. 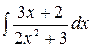 .
.
4.20. 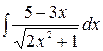 .
.
4.21. 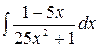 .
.
4.22. 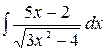 .
.
4.23. 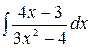 .
.
4.24. 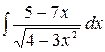 .
.
4.25. 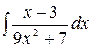 .
.
4.26. 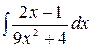 .
.
4.27. 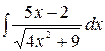 .
.
4.28. 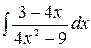 .
.
4.29. 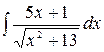 .
.
4.30. 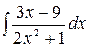 .
.
Задача № 5. Вычислить неопределенный интеграл от рациональной дроби, предварительно выделив целую часть.
5.1. 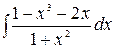 .
.
5.2. 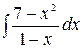 .
.
5.3. 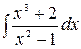 .
.
5.4. 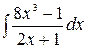 .
.
5.5. 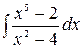 .
.
|
|
|
5.6. 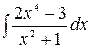 .
.
5.7. 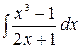 .
.
5.8. 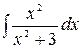 .
.
5.9. 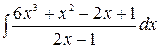 .
.
5.10. 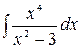 .
.
5.11. 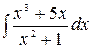 .
.
5.12. 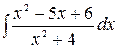 .
.
5.13. 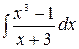 .
.
5.14. 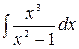 .
.
5.15. 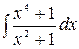 .
.
5.16. 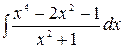 .
.
5.17. 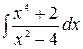 .
.
5.18. 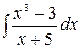 .
.
5.19. 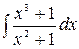 .
.
5.20. 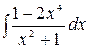 .
.
5.21. 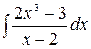 .
.
5.22. 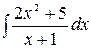 .
.
5.23. 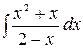 .
.
5.24. 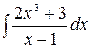 .
.
5.25. 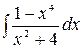 .
.
5.26. 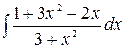 .
.
5.27. 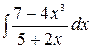 .
.
5.28. 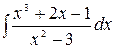 .
.
5.29. 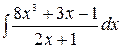 .
.
5.30. 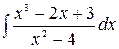 .
.
Задача № 6. Вычислить неопределенный интеграл методом интегрирования по частям.
6.1. 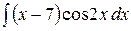 .
.
6.2. 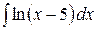 .
.
6.3. 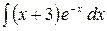 .
.
6.4. 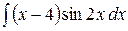 .
.
6.5. 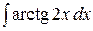 .
.
6.6. 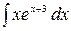 .
.
6.7. 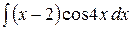 .
.
6.8. 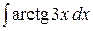 .
.
6.9. 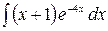 .
.
6.10. 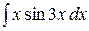 .
.
6.11. 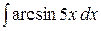 .
.
6.12. 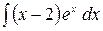 .
.
6.13. 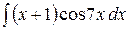 .
.
6.14. 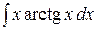 .
.
6.15. 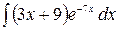 .
.
6.16. 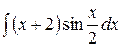 .
.
6.17. 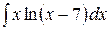 .
.
6.18. 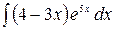 .
.
6.19. 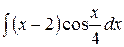 .
.
6.20. 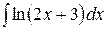 .
.
6.21. 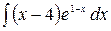 .
.
6.22. 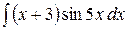 .
.
6.23. 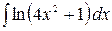 .
.
6.24. 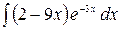 .
.
6.25. 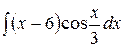 .
.
6.26.  .
.
6.27. 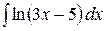 .
.
6.28. 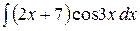 .
.
6.29. 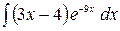 .
.
6.30. 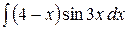 .
.
Задача № 7. Вычислить определенный интеграл методом замены переменной.
7.1. 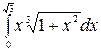 .
.
7.2. 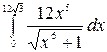 .
.
7.3. 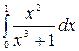 .
.
7.4. 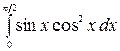 .
.
7.5. 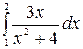 .
.
7.6. 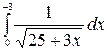 .
.
7.7. 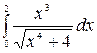 .
.
7.8. 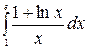 .
.
7.9. 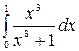 .
.
7.10. 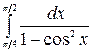 .
.
7.11. 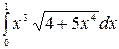 .
.
7.12. 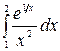 .
.
7.13. 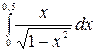 .
.
7.14. 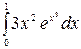 .
.
7.15. 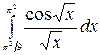 .
.
7.16. 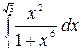 .
.
7.17. 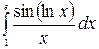 .
.
7.18. 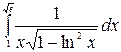 .
.
7.19. 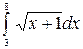 .
.
7.20. 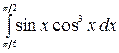 .
.
7.21. 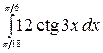 .
.
7.22. 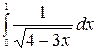 .
.
7.23. 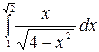 .
.
7.24. 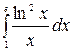 .
.
7.25. 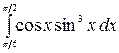 .
.
7.26. 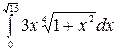 .
.
7.27. 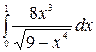 .
.
7.28. 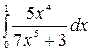 .
.
7.29. 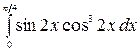 .
.
7.30. 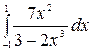 .
.
Задача № 8. Вычислить определенный интеграл методом интегрирования по частям.
8.1. 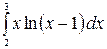 .
.
8.2. 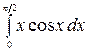 .
.
8.3. 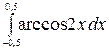 .
.
8.4. 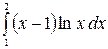 .
.
8.5. 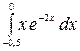 .
.
8.6. 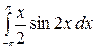 .
.
8.7. 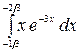 .
.
8.8. 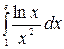 .
.
8.9. 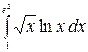 .
.
8.10. 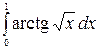 .
.
8.11. 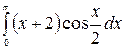 .
.
8.12. 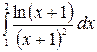 .
.
8.13. 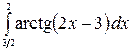 .
.
8.14. 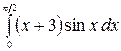 .
.
8.15. 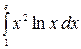 .
.
8.16. 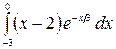 .
.
8.17. 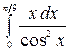 .
.
8.18. 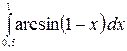 .
.
8.19. 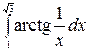 .
.
8.20. 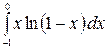 .
.
8.21. 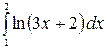 .
.
8.22. 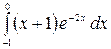 .
.
8.23. 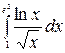 .
.
8.24. 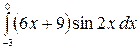 .
.
8.25. 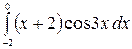 .
.
8.26. 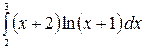 .
.
8.27. 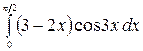 .
.
8.28. 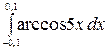 .
.
8.29. 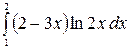 .
.
8.30. 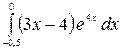 .
.
Задача № 9. Вычислить несобственный интеграл
9.1. 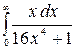 .
.
9.2. 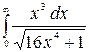 .
.
9.3. 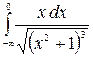 .
.
9.4. 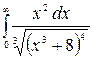 .
.
9.5. 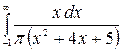 .
.
9.6. 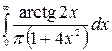 .
.
9.7. 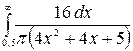 .
.
9.8. 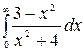 .
.
9.9. 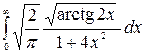 .
.
|
|
|
9.10. 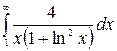 .
.
9.11. 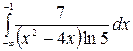 .
.
9.12. 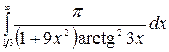 .
.
9.13. 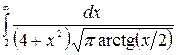 .
.
9.14. 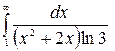 .
.
9.15. 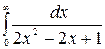 .
.
9.16. 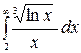 .
.
9.17. 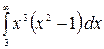 .
.
9.18. 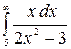 .
.
9.19. 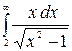 .
.
9.20. 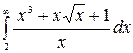 .
.
9.21. 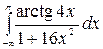 .
.
9.22. 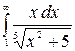 .
.
9.23. 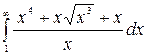 .
.
9.24. 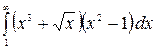 .
.
9.25. 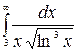 .
.
9.26. 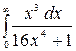 .
.
9.27. 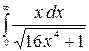 .
.
9.28. 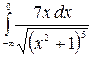 .
.
9.29. 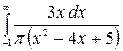 .
.
9.30. 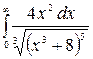 .
.
Задача № 10. Вычислить (с точностью до 0,01) площадь фигуры, ограниченной линиями
10.1. 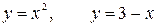 .
.
10.2.  .
.
10.3. 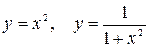 .
.
10.4. 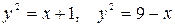 .
.
10.5. 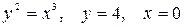 .
.
10.6. 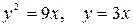 .
.
10.7. 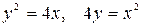 .
.
10.8. 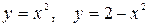 .
.
10.9. 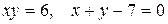 .
.
10.10. 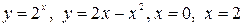 .
.
10.11. 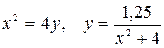 .
.
10.12. 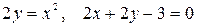 .
.
10.13. 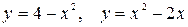 .
.
10.14. 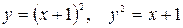 .
.
10.15. 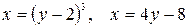 .
.
10.16. 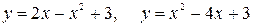 .
.
10.17. 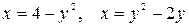 .
.
10.18. 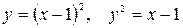 .
.
10.19. 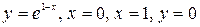 .
.
10.20. 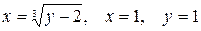 .
.
10.21. 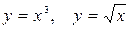 .
.
10.22. 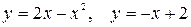 .
.
10.23. 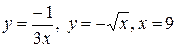 .
.
10.24. 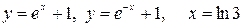 .
.
10.25. 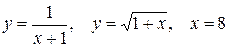 .
.
10.26. 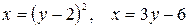 .
.
10.27. 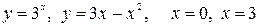 .
.
10.28. 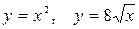 .
.
10.29. 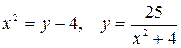 .
.
10.30. 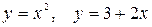 .
.
Задача № 11. Найти общее решение дифференциального уравнения с разделяющимися переменными.
11.1. а) 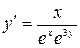 ; б)
; б) 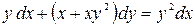 .
.
11.2. а) 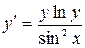 ; б)
; б) 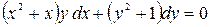 .
.
11.3. а) 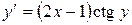 ; б)
; б) 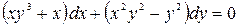 .
.
11.4. а) 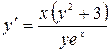 ; б)
; б) 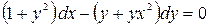 .
.
11.5. а) 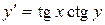 ; б)
; б) 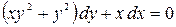 .
.
11.6. а) 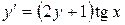 ; б)
; б) 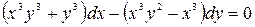 .
.
11.7. а) 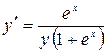 ; б)
; б) 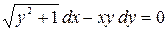 .
.
11.8. а) 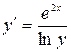 ; б)
; б) 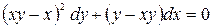 .
.
11.9. а) 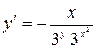 ; б)
; б) 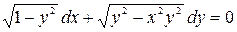 .
.
11.10. а) 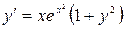 ; б)
; б) 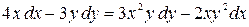 .
.
11.11. а) 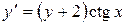 ; б)
; б) 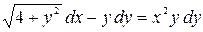 .
.
11.12. а) 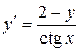 ; б)
; б) 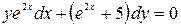 .
.
11.13. а) 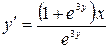 ; б)
; б) 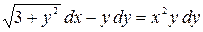 .
.
11.14. а) 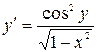 ; б)
; б) 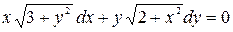 .
.
11.15. а) 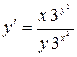 ; б)
; б) 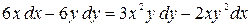 .
.
11.16. а) 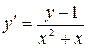 ; б)
; б) 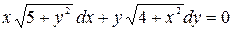 .
.
11.17. а) 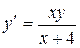 ; б)
; б) 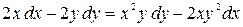 .
.
11.18. а) 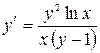 ; б)
; б) 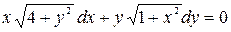 .
.
|
|
|
11.19. а) 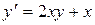 ; б)
; б) 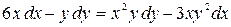 .
.
11.20. а) 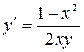 ; б)
; б) 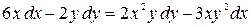 .
.
11.21. а) 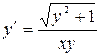 ; б)
; б) 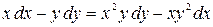 .
.
11.22. а) 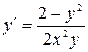 ; б)
; б) 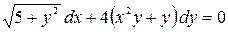 .
.
11.23. а) 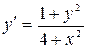 ; б)
; б) 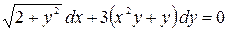 .
.
11.24. а) 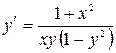 ; б)
; б) 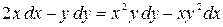 .
.
11.25. а) 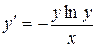 ; б)
; б) 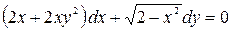 .
.
11.26. а) 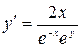 ; б)
; б) 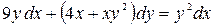 .
.
11.27. а) 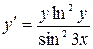 ; б)
; б) 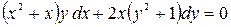 .
.
11.28. а) 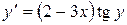 ; б)
; б) 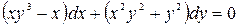 .
.
11.29. а) 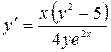 ; б)
; б) 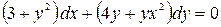 .
.
11.30. а) 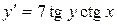 ; б)
; б) 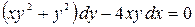 .
.
Задача № 12. Найти решение задачи Коши для линейного дифференциального уравнения.
12.1. 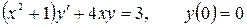 .
.
12.2. 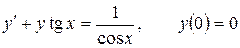 .
.
12.3. 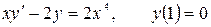 .
.
12.4. 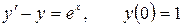 .
.
12.5. 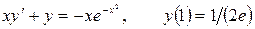 .
.
12.6. 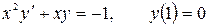 .
.
12.7. 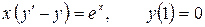 .
.
12.8. 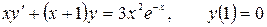 .
.
12.9. 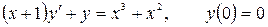 .
.
12.10. 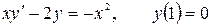 .
.
12.11.  .
.
12.12. 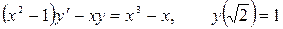 .
.
12.13. 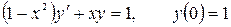 .
.
12.14. 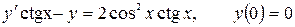 .
.
12.15. 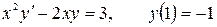 .
.
12.16. 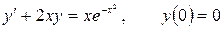 .
.
12.17. 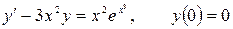 .
.
12.18. 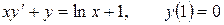 .
.
12.19. 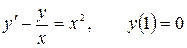 .
.
12.20. 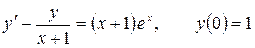 .
.
12.21. 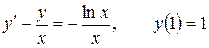 .
.
12.22. 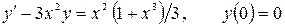 .
.
12.23. 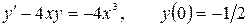 .
.
12.24. 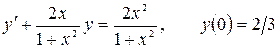 .
.
12.25. 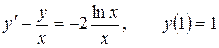 .
.
12.26. 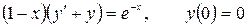 .
.
12.27. 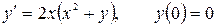 .
.
12.28. 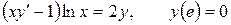 .
.
12.29. 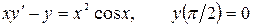 .
.
12.30. 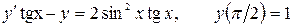 .
.
Задача № 13. Найти решение задачи Коши методом понижения порядка.
13.1. 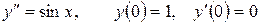 .
.
13.2. 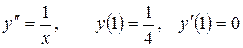 .
.
13.3. 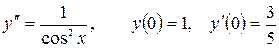 .
.
13.4. 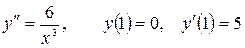 .
.
13.5. 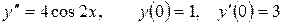 .
.
13.6. 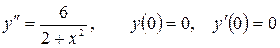 .
.
13.7. 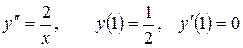 .
.
13.8. 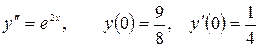 .
.
13.9. 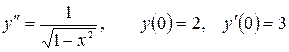 .
.
13.10. 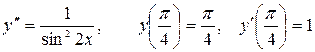 .
.
13.11. 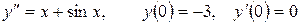 .
.
13.12. 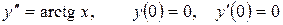 .
.
13.13. 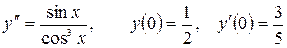 .
.
13.14. 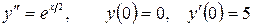 .
.
13.15. 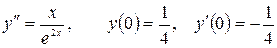 .
.
13.16. 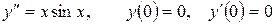 .
.
13.17. 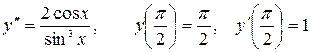 .
.
13.18. 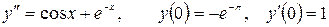 .
.
13.19.  .
.
13.20. 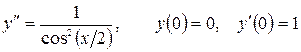 .
.
13.21. 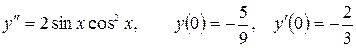 .
.
13.22. 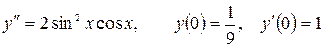 .
.
13.23. 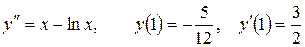 .
.
13.24. 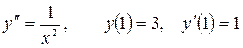 .
.
13.25. 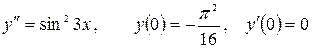 .
.
13.26. 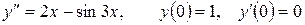 .
.
13.27. 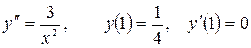 .
.
13.28. 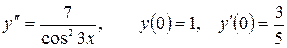 .
.
13.29. 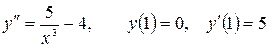 .
.
13.30. 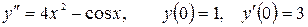 .
.
Задача № 14. Найти общее решение линейного однородного дифференциального уравнения с постоянными коэффициентами.
14.1. а) 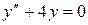 ;
;
б) 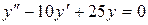 ;
;
в) 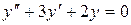 .
.
14.2. а) 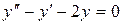 ;
;
б) 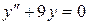 ;
;
в) 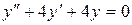 .
.
14.3. а) 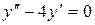 ;
;
б) 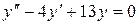 ;
;
|
|
|
в) 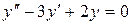 .
.
14.4. а) 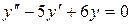 ;
;
б) 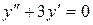 ;
;
в) 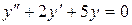 .
.
14.5. а) 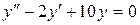 ;
;
б) 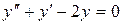 ;
;
в) 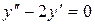 .
.
14.6. а) 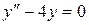 ;
;
б) 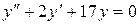 ;
;
в) 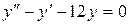 .
.
14.7. а) 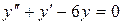 ;
;
б) 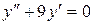 ;
;
в) 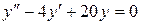 .
.
14.8. а) 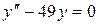 ;
;
б) 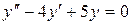 ;
;
в) 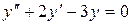 .
.
14.9. а) 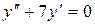 ;
;
б) 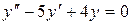 ;
;
в) 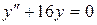 .
.
14.10. а) 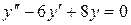 ;
;
б) 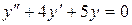 ;
;
в) 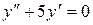 .
.
14.11. а) 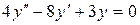 ;
;
б) 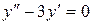 ;
;
в) 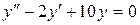 .
.
14.12. а) 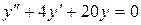 ;
;
б) 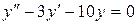 ;
;
в) 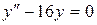 .
.
14.13. а) 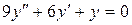 ;
;
б) 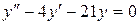 ;
;
в) 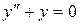 .
.
14.14. а) 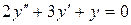 ;
;
б) 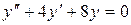 ;
;
в) 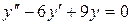 .
.
14.15. а) 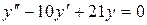 ;
;
б) 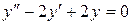 ;
;
в) 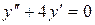 .
.
14.16. а) 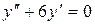 ;
;
б) 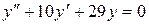 ;
;
в) 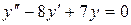 .
.
14.17. а) 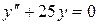 ;
;
б) 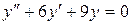 ;
;
в) 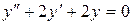 .
.
14.18. а) 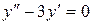 ;
;
б) 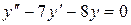 ;
;
в) 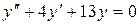 .
.
14.19. а) 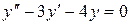 ;
;
б) 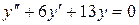 ;
;
в) 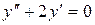 .
.
14.20. а) 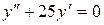 ;
;
б) 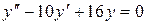 ;
;
в) 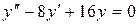 .
.
14.21. а) 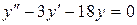 ;
;
б) 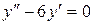 ;
;
в) 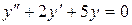 .
.
14.22. а) 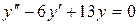 ;
;
б) 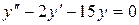 ;
;
в) 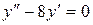 .
.
14.23. а) 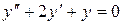 ;
;
б) 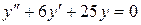 ;
;
в) 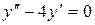 .
.
14.24. а) 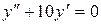 ;
;
б) 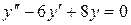 ;
;
в) 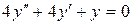 .
.
14.25. а) 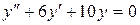 ;
;
б) 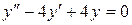 ;
;
в) 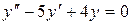 .
.
14.26. а) 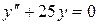 ;
;
б) 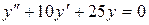 ;
;
в) 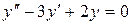 .
.
14.27. а) 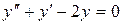 ;
;
б) 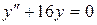 ;
;
в) 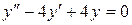 .
.
14.28. а) 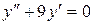 ;
;
б) 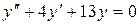 ;
;
в) 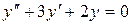 .
.
14.29. а) 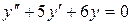 ;
;
б) 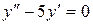 ;
;
в) 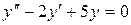 .
.
14.30. а) 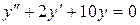 ;
;
б) 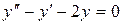 ;
;
в) 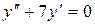 .
.
Задача № 15. Найти общее решение линейного неоднородного дифференциального уравнения с постоянными коэффициентами.
15.1. 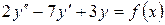 , если
, если
а) 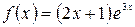 , б)
, б) 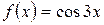 .
.
15.2. 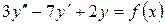 , если
, если
а) 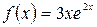 , б)
, б) 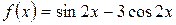 .
.
15.3. 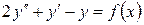 , если
, если
а) 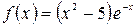 , б)
, б) 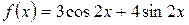 .
.
15.4. 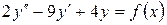 , если
, если
а) 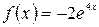 , б)
, б) 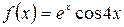 .
.
15.5. 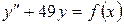 , если
, если
а) 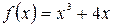 , б)
, б) 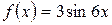 .
.
15.6. 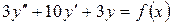 , если
, если
а) 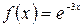 , б)
, б) 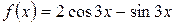 .
.
15.7. 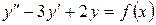 , если
, если
а) 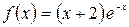 , б)
, б) 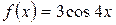 .
.
15.8. 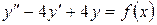 , если
, если
а) 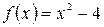 , б)
, б) 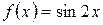 .
.
15.9. 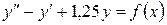 , если
, если
а) 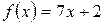 , б)
, б) 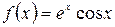 .
.
15.10. 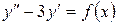 , если
, если
а) 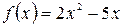 , б)
, б) 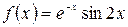 .
.
15.11. 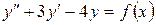 , если
, если
а) 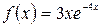 , б)
, б) 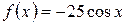 .
.
15.12. 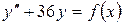 , если
, если
а) 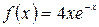 , б)
, б) 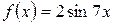 .
.
15.13. 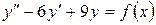 , если
, если
а) 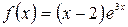 , б)
, б) 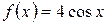 .
.
15.14. 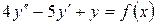 , если
, если
а) 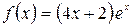 , б)
, б) 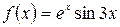 .
.
15.15. 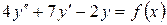 , если
, если
а) 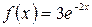 , б)
, б) 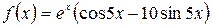 .
.
15.16. 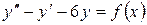 , если
, если
а) 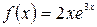 , б)
, б) 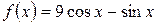 .
.
15.17. 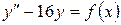 , если
, если
а) 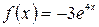 , б)
, б) 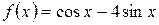 .
.
15.18. 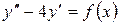 , если
, если
а) 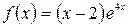 , б)
, б) 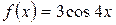 .
.
15.19. 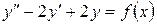 , если
, если
а) 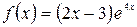 , б)
, б) 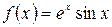 .
.
15.20. 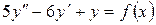 , если
, если
а) 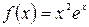 , б)
, б) 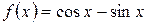 .
.
15.21. 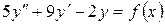 , если
, если
а) 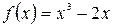 , б)
, б) 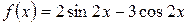 .
.
15.22. 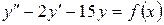 , если
, если
а) 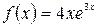 , б)
, б) 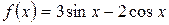 .
.
15.23. 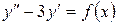 , если
, если
а) 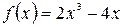 , б)
, б) 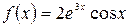 .
.
15.24. 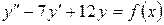 , если
, если
а) 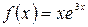 , б)
, б) 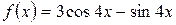 .
.
15.25. 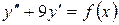 , если
, если
а) 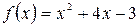 , б)
, б) 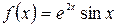 .
.
15.26. 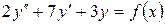 , если
, если
а) 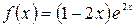 , б)
, б) 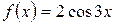 .
.
15.27. 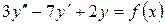 , если
, если
а) 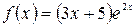 , б)
, б) 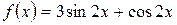 .
.
15.28. 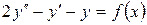 , если
, если
а) 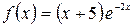 , б)
, б) 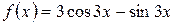 .
.
15.29. 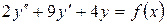 , если
, если
а) 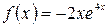 , б)
, б) 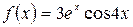 .
.
15.30. 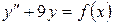 , если
, если
а) 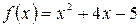 , б)
, б) 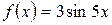 .
.
4. Решение типового варианта.
Задача № 1. Вычислить неопределенный интеграл
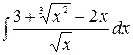 .
.
Решение. Представим подынтегральную функцию в виде суммы, разделив почленно числитель на 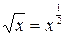 , а затем применим свойства и таблицу интегралов.
, а затем применим свойства и таблицу интегралов.
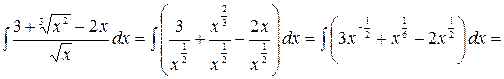
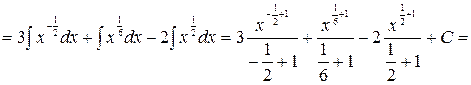
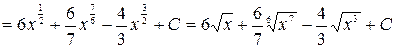 .
.
Задача № 2. Вычислить неопределенный интеграл
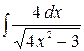 .
.
Решение. Приведем данный интеграл к табличному виду, воспользуемся свойством 6 и таблицей интегралов.
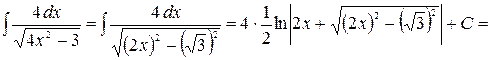
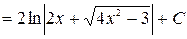 .
.
Задача № 3. Вычислить неопределенный интеграл
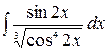 .
.
Решение. Учитывая, что 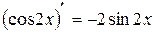 , то удобно выполнить замену переменной по формуле (1.1). Пусть
, то удобно выполнить замену переменной по формуле (1.1). Пусть 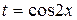 , тогда
, тогда 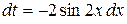 и
и 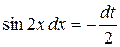 . Получим
. Получим
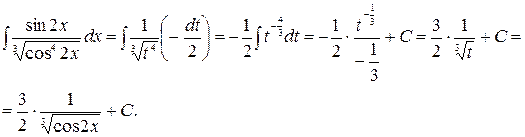
Задача № 4. Вычислить неопределенный интеграл
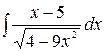 .
.
Решение. Представим данный интеграл в виде разности двух интегралов.
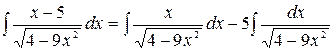 .
.
В первом интеграле выполним замену переменной: 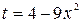 , тогда
, тогда 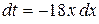 и
и 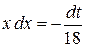 . Второй интеграл легко сводится к табличному. Получим:
. Второй интеграл легко сводится к табличному. Получим:
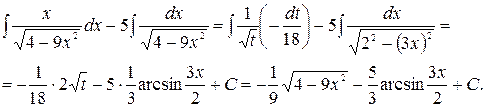
Задача № 5. Вычислить неопределенный интеграл
 .
.
Решение. Подынтегральная функция представляет собой неправильную рациональную дробь. Выделим целую часть дроби:
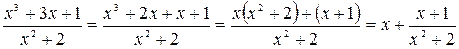 .
.
Получим
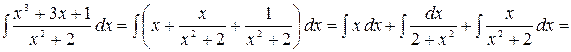
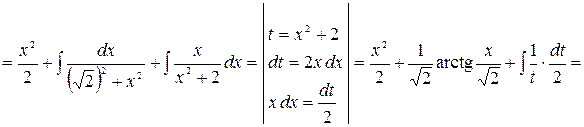
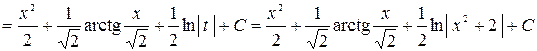 .
.
Задача № 6. Вычислить неопределенный интеграл
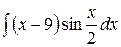 .
.
Решение. Для вычисления данного интеграла воспользуемся формулой интегрирования по частям (1.2). Положим: 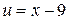 , а
, а 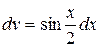 , тогда
, тогда 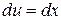 и
и 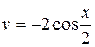 .
.
Получим
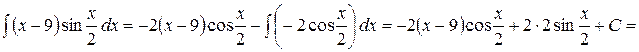
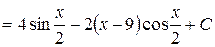 .
.
Задача № 7. Вычислить определенный интеграл
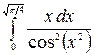 .
.
Решение. По формуле (1.5) выполним замену переменной в определенном интеграле. Пусть 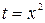 , тогда
, тогда 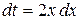 и
и 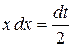 . Заменим пределы интегрирования:
. Заменим пределы интегрирования: 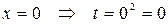 ,
, 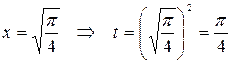 .
.
Применяя формулу Ньютона–Лейбница, получим
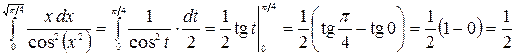 .
.
Задача № 8. Вычислить определенный интеграл
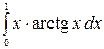 .
.
Решение. Воспользуемся формулой интегрирования по частям для определенного интеграла (1.4).
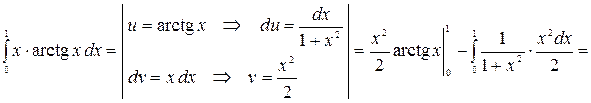
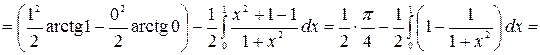
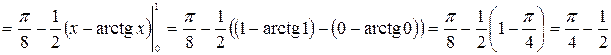 .
.
Задача № 9. Вычислить несобственный интеграл
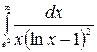 .
.
Решение. Выполним сначала замену переменной. Пусть 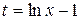 , тогда
, тогда 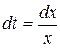 . Изменим пределы интегрирования:
. Изменим пределы интегрирования: 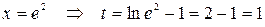 ,
, 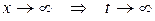 . Затем применим формулу (1.8). Получим
. Затем применим формулу (1.8). Получим
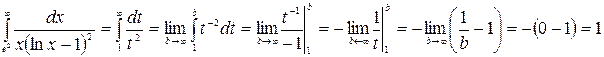 .
.
Задача № 10. Вычислить площадь фигуры, ограниченной линиями 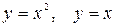 .
.
Решение. Определим пределы интегрирования. Для этого найдём точки пересечения графиков функций 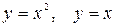 :
: 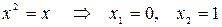 .
.
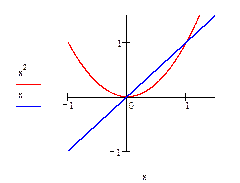
Фигура ограничена сверху графиком функции 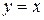 , снизу – графиком функции
, снизу – графиком функции 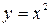 . Поэтому, согласно формуле (1.7) получим
. Поэтому, согласно формуле (1.7) получим
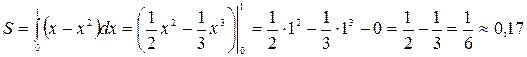 .
.
Ответ: 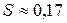 (кв.ед.)
(кв.ед.)
Задача № 11. Найти общее решение дифференциального уравнения
а) 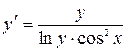 .
.
Решение. Учитывая, что 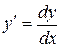 , сведем данное уравнение к уравнению с разделяющимися переменными:
, сведем данное уравнение к уравнению с разделяющимися переменными:
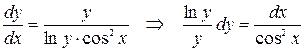 .
.
Интегрируем полученное уравнение:
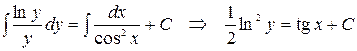 .
.
Общее решение в итоге имеет вид: 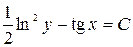 .
.
б) 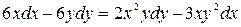 .
.
Решение. Преобразуем это уравнение к виду (2.1). Получим уравнение с разделяющимися переменными
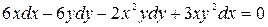 ,
,
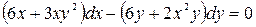 ,
,
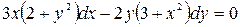 .
.
Разделим получившееся уравнение на 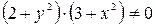 . Получим:
. Получим:
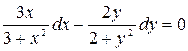 .
.
Проинтегрируем:
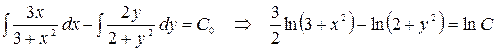 ,
,
где 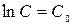 .
.
Применяя свойства логарифма, получим общее решение: 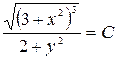 .
.
Задача № 12. Найти решение задачи Коши
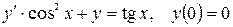 .
.
Решение. Данное уравнение является линейным. Преобразуем его к виду (2.5), разделив на 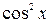 . Получим
. Получим
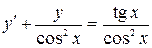 .
.
Решим это уравнение методом Бернулли. Выполним замену: 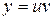 ,
, 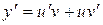 , где
, где 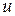 и
и 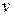 – неизвестные функции, одна из которых произвольная. Пусть
– неизвестные функции, одна из которых произвольная. Пусть 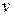 – произвольная функция, тогда после подстановки
– произвольная функция, тогда после подстановки 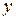 и
и 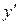 получим:
получим:
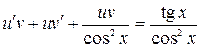 или
или 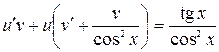 . (*)
. (*)
Одно из возможных значений 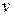 найдем из уравнения
найдем из уравнения
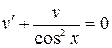 или
или 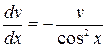 .
.
Разделяем переменные и интегрируем:
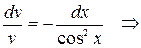
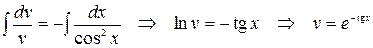 .
.
Подставим найденную функцию в уравнение (*) и найдем функцию 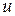 .
.
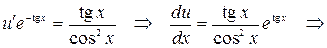
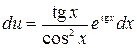 .
.
Интегрируя, получим
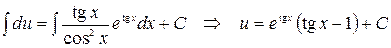 .
.
Искомое общее решение принимает вид
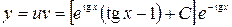 или
или 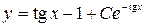 .
.
Найдем частное решение, удовлетворяющее начальному условию 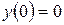
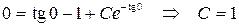 .
.
Тогда решение задачи Коши имеет вид: 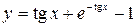 .
.
Задача № 13. Найти решение задачи Коши
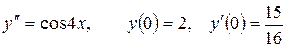 .
.
Решение. Это уравнение второго порядка. Его решение будем искать путем 2-кратного интегрирования:
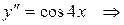
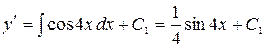 .
.
Найдем значение произвольной постоянной 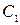 из условия
из условия 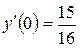 :
:
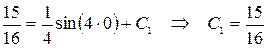 .
.
Тогда получим: 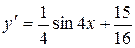 .
.
Интегрируя эту функцию, найдем общее решение исходного уравнения
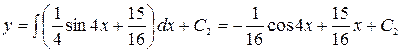 .
.
Определим значение 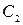 . Т.к.
. Т.к. 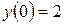 , то получим:
, то получим:
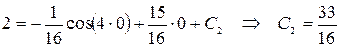 .
.
Решение задачи Коши, т.е. решение данного уравнения, удовлетворяющее начальным условиям, имеет вид:
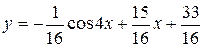 .
.
Задача № 14. Найти общее решение дифференциального уравнения
а) 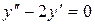 ; б)
; б) 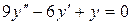 ; в)
; в) 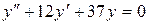 .
.
Решение. Данные уравнения являются линейными однородными уравнениями с постоянными коэффициентами. Общее решение имеет вид: 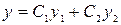 , где
, где 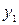 и
и 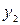 – частные решения этих уравнений и их вид зависит от решения характеристических уравнений.
– частные решения этих уравнений и их вид зависит от решения характеристических уравнений.
а) 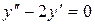 .
.
Составим и решим характеристическое уравнение:
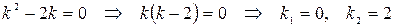 .
.
Т.к. корни уравнения действительные не совпадающие числа, то согласно (2.14) получим:
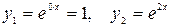 .
.
Общее решение имеет вид: 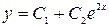 .
.
б) 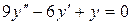 .
.
Решаем характеристическое уравнение:
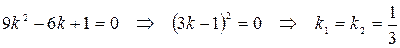 .
.
Получили совпадающие действительные корни и по формуле (2.15) имеем:
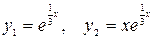 .
.
Получим общее решение: 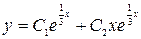 или
или 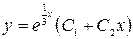 .
.
в) 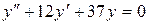 .
.
Решаем характеристическое уравнение:
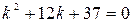
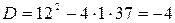
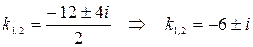 .
.
Получили комплексно сопряженные корни и согласно (2.16) имеем:
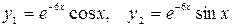 .
.
Общее решение имеет вид:
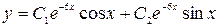 или
или 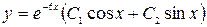 .
.
Задача № 15. Найти общее решение дифференциального уравнения
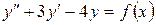 , если а)
, если а) 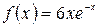 , б)
, б) 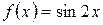 .
.
Решение. Данное уравнение является линейным неоднородным уравнением с постоянными коэффициентами. Структура общего решения, согласно (2.18) имеет вид: 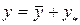 . Общее решение однородного уравнения, а именно
. Общее решение однородного уравнения, а именно 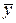 , в обоих случаях одно и то же. Найдем его, решая однородное уравнение
, в обоих случаях одно и то же. Найдем его, решая однородное уравнение 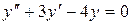 .
.
Решим характеристическое уравнение:
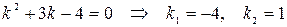 .
.
Тогда 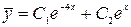 .
.
Найдем теперь 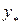 .
.
а) Так как 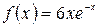 и
и 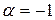 не является корнем характеристического уравнения, т.е. кратность его
не является корнем характеристического уравнения, т.е. кратность его 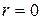 , и
, и 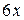 – многочлен первой степени, то по формуле (2.19) получим:
– многочлен первой степени, то по формуле (2.19) получим:
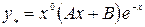 или
или 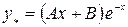 .
.
Для определения 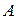 и
и 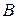 найдем
найдем 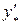 и
и 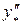 :
:
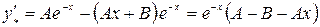 ,
,
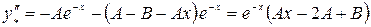 .
.
Подставим 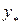 ,
, 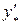 и
и 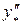 в исходное уравнение
в исходное уравнение
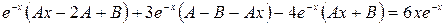 .
.
Сократим на 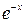 и приведем подобные слагаемые
и приведем подобные слагаемые
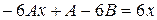 .
.
Приравняем коэффициенты при одинаковых степенях 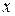 в левой и правой части и решим получившуюся систему
в левой и правой части и решим получившуюся систему
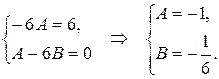
Тогда 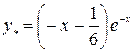 или
или 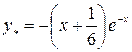 .
.
Общее решения принимает вид: 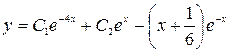 .
.
б) Функцию 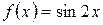 легко свести к специальному виду, а именно к виду
легко свести к специальному виду, а именно к виду 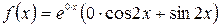 . Т.к.
. Т.к. 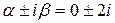 не является корнем характеристического уравнения, т.е. кратность его
не является корнем характеристического уравнения, т.е. кратность его 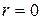 , то по формуле (2.20) получим
, то по формуле (2.20) получим
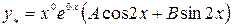 или
или 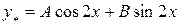 .
.
Найдем 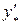 и
и 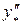 , и подставим
, и подставим 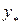 ,
, 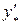 и
и 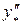 в исходное уравнение
в исходное уравнение
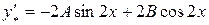 ;
; 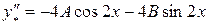 .
.
Тогда 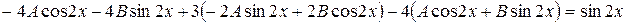 ,
,
или
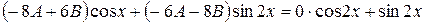 .
.
Приравниваем коэффициенты при одноименных тригонометрических функциях левой и правой частях. Решим получившуюся систему
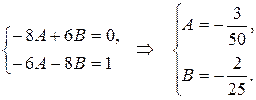
Тогда 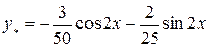 .
.
Запишем общее решение: 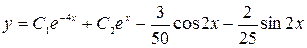 .
.
5. Литература.
а) Список использованной литературы
1. Сборник индивидуальных заданий по высшей математике. Ч. 2. Под ред. Рябушко А.П.– Минск: Вышэйшая школа, 1990.
2. Кузнецов Л.А. Сборник заданий по высшей математике. ТР. М.: Высшая школа, 1983 г., 2005 г.
3. Данко П.Е. и др. Высшая математика в упражнениях и задачах. Ч. 1; 2. М.: Высшая школа, 1980 г.
4. Пискунов Н.С. Дифференциальное и интегральное исчисление.
Т. 1; 2. М.: Наука, 1978 г.
б) Список рекомендуемой литературы
1. Пискунов Н.С. Дифференциальное и интегральное исчисление.
Т. 1; 2. М.: Наука, 1978 г.
2. Бугров Я.С., Никольский С.М. Дифференциальное и интегральное исчисление. М.: Наука, 1980 г.
3. Данко П.Е. и др. Высшая математика в упражнениях и задачах. Ч. 1; 2. М.: Высшая школа, 1980 г.
4. Письменый Д.Т. Конспект лекций по высшей математике: полный курс/Д.Т. Письменный. – 4-е изд. – М: Айрис-пресс, 2006. 608 с.
5. Зимина О.В., Кириллов А.И., Сальникова Т.А. Высшая математика. ( Серия "решебник") 2-е изд., испр. – М.: Физико-математическая литература, 2001. – 368 с. (Решебник.) URL: http://www.alleng.ru/d/math/math164.htm
6. Запорожец Г.И. Руководство к решению задач по математическому анализу. 4-е изд., М.: Высшая школа, 1966. - 464с. URL: http://www.alleng.ru/d/math/math24.htm
7. Смолянский М.Л. Таблицы неопределенных интегралов. 2-е изд., испр. - М.: Гос. изд. физ-мат. лит., 1963. - 112с. URL: http://www.alleng.ru/d/math/math208.htm
Оглавление
1. Интегральное исчисление функции одного действительного
аргумента …………………………………………………………......3
2. Дифференциальные уравнения…………………………………..….9
3. Индивидуальные задания для контрольной работы………………14
4. Решение типового варианта……………………………………..….35
5. Литература………………………………………………………...…46
Дата добавления: 2021-01-21; просмотров: 42; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
