Дифференциальные уравнения первого порядка.
Уравнение вида 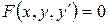 , где
, где 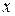 – независимая переменная,
– независимая переменная, 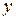 – искомая функция,
– искомая функция, 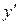 – её производная, называется дифференциальным уравнением первого порядка.
– её производная, называется дифференциальным уравнением первого порядка.
Решением дифференциального уравнения первого порядка называется функция, которая при подстановке в уравнение превращает его в тождество.
Условие, что при 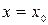 функция
функция 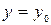
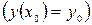 называется начальным условием.
называется начальным условием.
Функция, 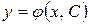 , содержащая одну произвольную постоянную называется общим решением. Функция
, содержащая одну произвольную постоянную называется общим решением. Функция 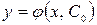 , полученная из общего решения и удовлетворяющая начальному условию, называется частным решением.
, полученная из общего решения и удовлетворяющая начальному условию, называется частным решением.
Рассмотрим методы интегрирования некоторых уравнений первого порядка.
Уравнение с разделяющимися переменными – это уравнение вида:
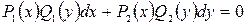 , (2.1)
, (2.1)
где  ,
,  ,
,  и
и  – известные функции, зависящие только от
– известные функции, зависящие только от 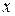 или
или 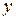 .
.
Если ни одна из этих функций не равна тождественно нулю, то разделив уравнение (2.1) на 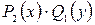 , получим уравнение с разделенными переменными:
, получим уравнение с разделенными переменными:
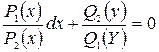 . (2.2)
. (2.2)
Проинтегрировав это уравнение, получим общее решение исходного уравнения:
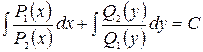 . (2.3)
. (2.3)
Уравнение 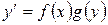 сводится к уравнению с разделенными переменными. Учитывая, что
сводится к уравнению с разделенными переменными. Учитывая, что 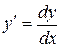 , получим уравнение вида:
, получим уравнение вида:
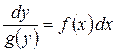 . (2.4)
. (2.4)
Линейное уравнение – это уравнение вида:
 , (2.5)
, (2.5)
|
|
|
где 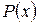 и
и 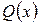 – заданные функции.
– заданные функции.
Для решения его рассмотрим метод Бернулли. Выполним подстановку 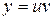 , где
, где 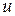 и
и 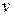 – две неизвестные функции, причем одна из которых произвольная. Тогда уравнение (2.5) сводится у виду
– две неизвестные функции, причем одна из которых произвольная. Тогда уравнение (2.5) сводится у виду
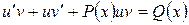 или
или 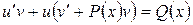 . (2.6)
. (2.6)
Предполагая, что 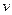 – произвольная функция, найдем одно из ее решений из уравнения
– произвольная функция, найдем одно из ее решений из уравнения 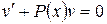 , например,
, например,
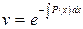 . (2.7)
. (2.7)
Тогда уравнение (2.6) сведется к виду:
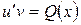 или
или 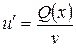 , т.е.
, т.е.  . (2.8)
. (2.8)
Решая уравнение (2.8), получим:
 . (2.9)
. (2.9)
Общее решение исходного уравнения находится умножением 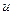 на
на 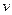 :
:
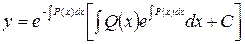 . (2.10)
. (2.10)
Дифференциальные уравнения второго порядка.
Общий вид уравнения второго порядка: 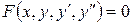 .
.
Начальные условия принимают вид: 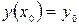 и
и 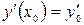 .
.
Общим решением является функция 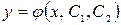 , содержащая две произвольных постоянных
, содержащая две произвольных постоянных 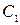 и
и 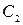 . Частным решением называется функция
. Частным решением называется функция 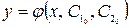 , полученное из общего решения, удовлетворяющее начальным условиям.
, полученное из общего решения, удовлетворяющее начальным условиям.
Рассмотрим только некоторые уравнения второго порядка.
Уравнения вида  . Решение этого уравнения находится 2-кратным интегрированием, а именно:
. Решение этого уравнения находится 2-кратным интегрированием, а именно:  ,
,
|
|
|
 ,
, 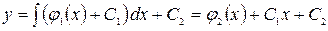 . (2.11)
. (2.11)
Линейные однородные уравнения с постоянными коэффициентами. Это уравнения вида:
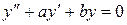 , (2.12)
, (2.12)
где 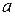 и
и 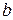 – некоторые действительные числа.
– некоторые действительные числа.
Общим решением является функция 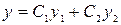 , где
, где 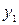 и
и 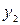 – частные решения уравнения (2.12). Для их определения решаем характеристическое уравнение
– частные решения уравнения (2.12). Для их определения решаем характеристическое уравнение
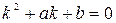 . (2.13)
. (2.13)
Пусть  и
и 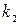 – корни уравнения (2.13), тогда возможны следующие случаи:
– корни уравнения (2.13), тогда возможны следующие случаи:
1) если  и
и 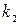 – действительные числа, причем
– действительные числа, причем 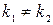 , тогда:
, тогда:
 и
и 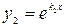 ; (2.14)
; (2.14)
2) если  и
и 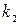 – действительные числа, и
– действительные числа, и 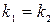 , тогда:
, тогда:
 и
и  ; (2.15)
; (2.15)
3) если  и
и 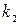 – комплексные числа, т.е.
– комплексные числа, т.е. 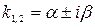 , тогда:
, тогда:
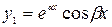 и
и 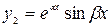 . (2.16)
. (2.16)
Линейные неоднородные уравнения с постоянными коэффициентами. Уравнения имеют вид:
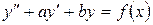 , где
, где  – заданная функция. (2.17)
– заданная функция. (2.17)
Структура общего решения уравнения (2.17) определяется следующим образом:
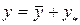 , (2.18)
, (2.18)
где 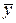 – общее решение однородного уравнения (2.12), которые определяются по формулам (2.14)–(2.16), а
– общее решение однородного уравнения (2.12), которые определяются по формулам (2.14)–(2.16), а 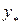 – частное решение уравнения (2.17).
– частное решение уравнения (2.17).
|
|
|
Метод нахождения частного решения 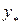 зависит от функции
зависит от функции  . Остановимся только на случае, когда
. Остановимся только на случае, когда  – функция специального вида.
– функция специального вида.
1) Пусть  , где
, где 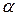 – действительное число, а
– действительное число, а 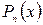 – многочлен степени
– многочлен степени 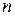 . Частное решение ищем в виде
. Частное решение ищем в виде
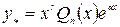 , (2.19)
, (2.19)
где  – число, равное кратности
– число, равное кратности 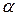 как корня характеристического уравнения (2.13), а
как корня характеристического уравнения (2.13), а 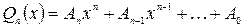 – многочлен степени
– многочлен степени 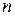 с неопределенными коэффициентами
с неопределенными коэффициентами  .
.
Для определения этих коэффициентов, подставим 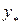 в уравнение (2.17), сократим на
в уравнение (2.17), сократим на 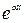 . Получим слева многочлен степени
. Получим слева многочлен степени 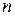 с неопределенными коэффициентами
с неопределенными коэффициентами  , справа – многочлен степени
, справа – многочлен степени 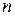 , но с известными коэффициентами. Приравнивая коэффициенты при одинаковых степенях
, но с известными коэффициентами. Приравнивая коэффициенты при одинаковых степенях 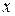 , получим систему алгебраических уравнений для определения коэффициентов
, получим систему алгебраических уравнений для определения коэффициентов  .
.
2) Пусть 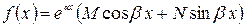 , где
, где 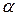 ,
, 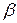 ,
,  и
и  – действительные числа. Тогда частное решение ищем в виде
– действительные числа. Тогда частное решение ищем в виде
 , (2.20)
, (2.20)
где  – число, равное кратности
– число, равное кратности  как корня характеристического уравнения (2.13), а
как корня характеристического уравнения (2.13), а 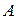 и
и 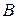 – неопределенные коэффициенты.
– неопределенные коэффициенты.
После подстановки 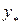 в уравнение (2.17) и сократив на
в уравнение (2.17) и сократив на 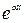 , приравниваем коэффициенты, стоящие перед одноименными тригонометрическими функциями в левой и правой части уравнения.
, приравниваем коэффициенты, стоящие перед одноименными тригонометрическими функциями в левой и правой части уравнения.
|
|
|
Замечание: форма (2.20) частного решения сохраняется и в случаях, когда  или
или  .
.
Дата добавления: 2021-01-21; просмотров: 80; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
