Вычисления угла между прямыми

⇐ ПредыдущаяСтр 2 из 2

1. Ax+By+C=0

2. y=kx+b;

tga=|(k2-k1)/(1+k1k2)|

k1k2=1 - условие перпендекулярности;

3. (x-x0)/m=(y-y0)/p;

cosa=(m1m2+p1p2)/((m1²+p1²)^1/2(m2²+p2²)^1/2)

m1m2+p1p2=0 - условие перпендекулярности;

Линии второго порядка. Эллипс

Алгебраической кривой 2 порядка называется кривая заданая уравнением:

Ax²+2Bxy+Cy²+Dx+Ey+F=0;

где A,B,C не равны нулю одновременно.

A,B,C,D,E,F - const.

Замечание: в общем случае может оказаться, что данное уравнение второй степени определяет вырожденную кривую(точка, пара прямых, пустое множество, мнимая фигура).

Если данная кривая невырожденная, то ...2B(xy)... обозначает поворот.

Эллипсом называется множество точек плоскости, сумма расстояний которых до двух данных точек, называемых фокусами и есть величина постоянная.

Линии второго порядка. Гипербола

Гиперболой называется множество всех точек плоскости, для каждой из которых модуль разности расстояний до двух данных точек этой плоскости, называемых фокусами, есть величина постоянная, меньшая, чем расстояние между фокусами.

В данном случае Ox - действительная ось, Oy - мнимая ось.

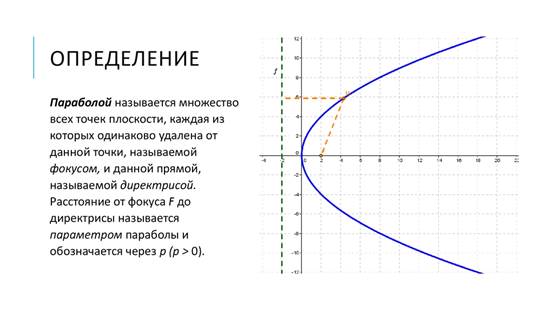
Линии второго порядка. Парабола

Понятие поверхности второго порядка

Поверхностью второго порядка называется поверхность, определяемая уравнением:

ax²+by²+cz²+dxy+fxz+qyz+hz+ky+lz+m=0;

где a,b,c,d,f,g,h,k,l,m - вещественные числа, причём хотя бы одно из чисел a,b,c,d,f,g - отличны от нуля.

Эллипсойд

Эллипсоид — поверхность в трёхмерном пространстве, полученная деформацией сферы вдоль трёх взаимно перпендикулярных осей.

x²/a²+y²/b²+z²/c²=1;

Если равны все три значения (a=b=c) ,то поверхностью будет сфера, радиус которой r.

Гиперболоиды

Гиперболойд— это вид поверхности второго порядка в трёхмерном пространстве, задаваемый в декартовых координатах уравнением

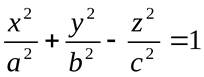(однополостный гиперболоид),

где a и b — действительные полуоси, а c — мнимая полуось;

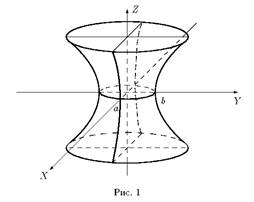
или

(двуполостный гиперболоид),

где a и b — мнимые полуоси, а c — действительная полуось.

Параболойды

Исследование уравнений поверхностей методом параллельных сечений

Если задано уравнение той или иной поверхности, то возникает задача исследования ее формы и расположения относительно координатных осей.

Для решения этой задачи обычно применяют метод параллельных сечений, который состоит в том, что поверхность пересекается несколькими плоскостями, параллельными плоскостям координат. Форма и размеры полученных сечений позволяют выяснить форму самой поверхности.

Рассмотрим этот метод на примерах.

Исследовать сечения эллипсоида 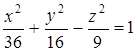плоскостями

Решение. Рассмотрим сначала сечение эллипсоида плоскостями 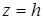, где

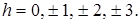Подставляя в уравнение эллипсоида, получим

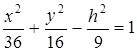или ,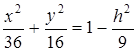

Отсюда

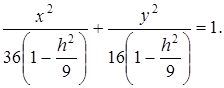
Обозначив 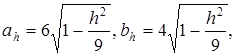получим в сечении эллипс

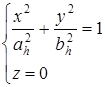
С полуосями .

При получаем:

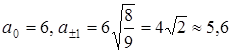
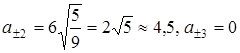
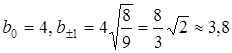
Таким образом наибольший эллипс получается в сечении плоскости 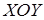. Если поднимать или опускать эту плоскость вдоль оси . Параллельно плоскости

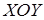, то размеры сечений уменьшаются до тех пор, пока при 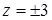не превратятся в точку 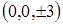. При дальнейшем увеличении 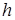плоскость эллипсоида пересекать уже не будет, так как корень, входящий в выражение для

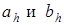, станет мнимым.

В сечении плоскостями, параллельными , будут также получаться эллипсы. В частности, в сечении координатными плоскостям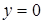и и

получатся наибольшие по размерам эллипсы.

и .

Проведенное исследование позволяет сделать вывод, что эллипсоид является овальной поверхностью .

Дата добавления: 2021-01-21; просмотров: 68; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 12

Мы поможем в написании ваших работ!