Предпочтения потребителя и его функция полезности

Статистические модели экономики

Модель Леонтьева

Рассмотрим статическую линейную модель многоотраслевой экономики. В основе модели лежат следующие предположения:

в экономической системе производятся, продаются, покупаются, потребляются и инвестируются n продуктов;

каждая отрасль является «чистой», т.е. производит только один продукт, совместное производство различных продуктов исключается. Различные отрасли выпускают разные продукты;

под производственным процессом в каждой отрасли понимается преобразование некоторых (возможно, всех) типов продуктов в определенный продукт. При этом соотношение затраченного продукта и выпускаемого предполагается постоянным. Таким образом, если для производства единицы j-го продукта надо затратить а_ij единиц i-го продукта, то выпуск λ единиц j-го продукта потребует λ а_ij единиц i-го продукта.

Итак, независимо от масштаба производства удельный выпуск и соотношение затрат предполагаются постоянными.

Валовой выпуск i-го продукта за год х_i распадается на две части: на производственное потребление во всех отраслях и на конечное (непроизводственное) потребление.

В предположениях 1-3 производственное потребление i-го продукта всеми отраслями равно 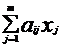, поэтому чистый выпуск j-го продукта составит

x_j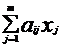_- , i = 1, …, n, (1.1)

Если приравнять чистый выпуск каждого i-го продукта и конечный спрос на него y_i_, то образуется система уравнений:

x_j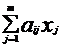_- = y_i_,i = 1, …, n, (1.2)

которая и составляет модель Леонтьева.

Конечный спрос и состоит из конечного потребления, экспорта и инвестиций. Однако в самой модели величины у_i мыслятся как экзогенно заданные. Поэтому при заданных у_i, i = 1,…, n, n линейных уравнений модели Леонтьева позволяют определить n отраслевых выпусков х_i, i = 1,…, n.

Таким образом, сущность метода Леонтьева состоит в определении валового выпуска отраслей по заданному экзогенно конечному спросу на основе данных о технологических возможностях, воплощенных в расходных коэффициентах а_ij. Разумеется, по этим же уравнениям может быть решена и обратная задача: по заданным валовым выпускам определяются объемы конечного спроса y_i на каждый продукт.

Величины х_i, у_i: могут быть представлены в натуральных или стоимостных единицах измерения, в соответствии с этим различают натуральный или стоимостный межотраслевые балансы.

Система (1.2) - это система п линейных уравнений с п неизвестными х_i, i = 1,…, п, которая является хорошо изученным объектом линейной алгебры. Однако система описывает отраслевую структуру экономики и поэтому обладает следующими свойствами: коэффициенты прямых затрат а_ij, объемы конечного спроса у_i, и валовые выпуски x_i - неотрицательны. Система (1.2) называется работоспособной или продуктивной если она разрешима в неотрицательных х_i_, т, е. 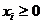, i = 1,…, n. Двойственной к системе (1.2) называется следующая система линейных уравнений для цен продуктов р_j:

, j=1,…, n, (1.3)

где - добавленная стоимость на единицу выпускаемой j-й отрасли.

Поскольку 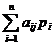- сумма издержек на единицу выпуска j-й отрасли, то в левой части каждого из уравнений (1.3) стоит чистый доход от единичного выпуска j-й отрасли, который и приравнивается, к добавленной стоимости .

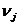Система (1.3) называется прибыльной, если она разрешима в неотрицательных 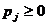, j = 1, …, n. Можно доказать, что продуктивность (1.2) и прибыльность (1.3) эквивалентны: из продуктивности (1.2) следует прибыльность (1.3), и наоборот.

Квадратная матрица D называется неотрицательно обратимой, если D невырождена и ее обратная матрица неотрицательна.

Система (1.2) может быть записана в матричной форме:

(1-А) х = у, (1.4)

где I = I_n - единичная матрица с размерами

n x n, x = (x_i, …, x_n)¢, y=(y_i,…, y_n)^¢

Из (1.4) видно, что условие продуктивности (1.2) эквивалентно неотрицательной обратимости матрицы (I - A). Если одно из этих условий выполнено, то

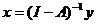, (1.5)

причем 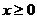, т.е. задача определения вектора неотрицательного конечного спроса у решена.

Обозначим через N множество номеров отраслей= {1, 2,…, n}. Подмножество отраслей S изолировано, если а_ij= 0

для , 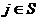. Это означает, что отрасли S не нуждаются в товарах, производимых другими отраслями 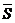, хотя, быть может, передают им свои товары. Если перенумеровать отрасли так, чтобы первыми располагались k отраслей S, то матрица А примет следующий вид:

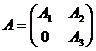, (1.6)

где А₁ - квадратная матрица с размерами k х k, отвечающая отраслям S;

А₃ - квадратная матрица с размерами (n-k) x (n-k), соответствующая; отраслям .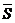

Технологическая матрица называется неразложимой, если ее нельзя путем перестановок строк и столбцов привести к виду (1.6). Неразложимость А означает, что каждая отрасль хотя бы косвенно использует продукцию всех отраслей.

Для неразложимой матрицы имеет место теорема Фробениуса - Перрона:

. Неразложимая матрица А имеет положительное собственное число l_A>0, которое превосходит модули всех остальных собственных чисел.

. Собственному числу l_A отвечает единственный собственный вектор х_A (с точностью до скалярного множителя), все координаты которого ненулевые и имеют один знак (т.е. его всегда можно выбрать положительным за счет скалярного множителя).

Опираясь на теорему Фробениуса - Перрона можно доказать следующую важную для приложений теорему: модель Леонтьева продуктивна тогда и только тогда, когда l_A < 1.

Достаточность. Поскольку

Ax_A =l_A x_A_, x_A>0, 0 < l_A < 1, то А^kx_A=А^k^-1(Ax_A)= l_A(А^k^-1x_A) =

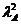= (А^k^-2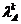x_A)=…= x_A,

поэтому 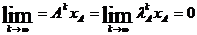. Но х_А>0, А^k³ 0, следовательно .

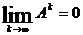Рассмотрим математическое равенство, которое легко проверить, если раскрыть скобки в левой части:

(I-A) (I+A+A²+ … +A^k-1) = I - A^k, (1.7)

Поскольку предел правой части при k ®¥ равен I, то существует и предел левой части. Таким образом, 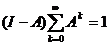, т.е. обратная матрица 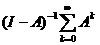существует и для нее имеет место разложение, аналогичное сумме бесконечной геометрической прогрессии. Кроме того, так как все A^k³ 0, то (I-А)^-1³ 0, поэтому для любого вектора конечного спроса у ³ 0 существует неотрицательное решение системы уравнений:

х = (I-А)^-1y (1.8)

т.е. модель Леонтьева продуктивна.

1.2 Модели определения оптимального плана предприятия, относящегося к задачам целочисленного программирования

Более целесообразно целочисленное программирование было бы назвать дискретным программированием. Это есть часть математического программирования, занимающаяся исследованием экстремальных задач на целочисленных решетках и конечных множествах. В терминах дискретного программирования формализуются многие важные задачи экономики, управления, планирования, проектирования, а так же ряд других задач, например: размещение и специализация предприятий; оптимизация комплекса технических средств доставки грузов; важные сельскохозяйственные задачи и т.д.

Рассмотрим задачу математического программирования, в которой требуется, чтобы все переменные принимали целые неотрицательные значения.

Максимизировать линейную функцию

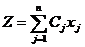, (1.9)

при условиях

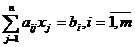, (1.10)

x_j = 0, или 1, или 2, или 3, …; , (1.11)

причем , b_i. предполагаются целыми числами.

Симплекс-метод приводит непосредственно к целочисленному решению лишь для немногих задач. В общем же случае требуются специальные методы, заключающиеся в подборе дополнительных линейных ограничений к системе ограничений (1.10), обеспечивающих целочисленность решения.

Один из таких методов, приводящий к целочисленному решению за конечное число шагов, предложен Р.Е. Гомори.

Предположим, что задача линейного программирования имеет многоугольник (многогранник) допустимых решений.

Рис. 1.1. Многоугольник (многогранник) допустимых решений

Если наложить требование целочисленности, то допустимое множество решений вырождается в систему точек и уже в общем случае не является выпуклым. Если добавить новые ограничения, связывающие внешние целочисленные точки, а затем в качестве многоугольника (многогранника) решений использовать все выпуклое множество, то получим новую задачу линейного программирования со следующими свойствами:

новый многоугольник решений содержит все целые точки, заключавшиеся в первоначальном многоугольнике (многограннике) решений; любая угловая его точка является целой;

- так как линейная функция достигает оптимума в угловой точке многоугольника (многогранника) решений, то построением такого многоугольника и обеспечивается целочисленность оптимального решения.

Решение поставленной задачи ведем симплексным методом без учета требования целочисленности. Если оптимальный план целочисленный, то вычисления заканчивают; если же в оптимальном решении такой задачи хотя бы одна компонента не будет целым числом, то вводятся дополнительные ограничения и процесс решения продолжается.

Предположим, что, максимизируя (1.9) при условиях (1.10) и (1.11) без учета требования целочисленности переменных мы пришли к оптимальному решению с предпочитаемым эквивалентом системы ограничений (1.10) вида:

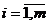, , (1.12)

Пусть правые части f_i некоторых уравнений оказалиcm дробными. Выберем одну из них, например f₁. Каждый коэффициент е₁_j при неизвестной в соответствующем уравнении системы и свободный член f₁ представим в виде суммы целой части и правильной неотрицательной дроби

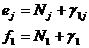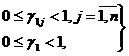, (1.13)

помня, что целой частью любого числа называется наибольшее целое число, не превосходящее данного числа. Тогда соответствующее уравнение системы можно записать:

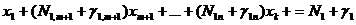или

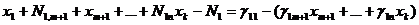, (1.14)

где k = n + m.

Левая часть этого равенства должна быть числом целым, так как мы требуем, чтобы все переменные принимали целые неотрицательные значения. Поэтому и правая часть должна быть целым числом и, очевидно, это число не больше, чем 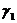. Но 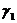есть правильная неотрицательная дробь и, следовательно, правая часть не может превышать нуля:

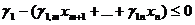, (1.15)

откуда

(1.16)

Вычитая из левой части новую неотрицательную неизвестную х_n₊₁, заменим неравенство (d) уравнением:

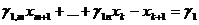, или

, (1.17)

где 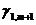, ,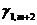… коэффициенты, стоящие в первой строке оптимальной, но нецелочисленной таблицы, и под неизвестными х_m ₊ ₁, х_m ₊ _2,….

Это и есть дополнительное ограничение, которое следует ввести. Новая задача с (m + 1) уравнениями (1.10) и (1.17) является задачей дискретного программирования, так как 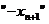совпадает с правой частью равенства (1.14). На данном этапе значение х_n ₊ ₁ равно , т.е. отрицательно и дробно. Мы добавляем к последней симплексной таблице еще одну строку, соответствующую уравнению (1.17). При этом относительные оценочные коэффициенты не изменяются, т.е. условие оптимальности сохраняется.

Возобновляя процесс преобразования симплексных таблиц, применим двойственный метод и переведем неизвестную х_n₊₁ из базисных в свободную. Возможно, что после этого получится базисное неотрицательное решение с целочисленными компонентами и задача решена. Если нет, то составляем следующее дополнительное ограничение, учитывающее целочисленность. Процесс присоединения дополнительных ограничений повторяют до тех пор, пока либо будет найден целочисленный оптимальный план, либо будет доказано, что задача не имеет целочисленных планов. Если имеются несколько дробных f_i, то дополнительное ограничение (1.17) составляют для mах 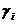. Это ускоряет процесс получения оптимального целочисленного решения.

Предпочтения потребителя и его функция полезности

Одним из важных понятий экономической теории является домашнее хозяйство (потребитель). Главная проблема при изучении поведения потребителя заключается в том, чтобы установить, в каких объемах он приобретет наличные товары и услуги при заданных ценах и доходе.

Конкретное решение потребителя о покупке определенного набора товаров математически можно представить как выбор конкретной точки в пространстве товаров. Пусть п - конечное число рассматриваемых товаров; х = (х_1,…, х₂)' - вектор-столбец объемов товаров, приобретенных потребителем за определенный срок (например, за год) при заданных ценах и доходе за тот же срок. Пространство товаров - это множество всевозможных наборов товаров х с неотрицательными координатами: С ={х: x ³ 0}.

В теории потребительского выбора предполагается, что каждый Потребитель изначально имеет свои предпочтения на некотором подмножестве пространства товаров 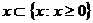, Это означает, что для каждой пары 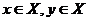имеет место одно из трех отношений:

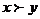- набор х предпочтительнее у;

- набор x менее предпочтителен, чем;

x~y - для потребителя оба набора обладают одинаковой степенью предпочтения.

Отношения предпочтения обладают, по крайней мере следующими свойствами:

1) если 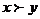, , 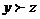то (транзитивность);

) если х > у, то 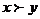(ненасыщаемостъ; больший набор всегда предпочтительнее меньшего).

Отношения предпочтения каждого потребителя при определенных слабых предположениях, касающихся предпочтений, можно (и удобно!) представить в форме индикатора предпочтений, т.е. такой функции полезности и(х), что из 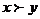следует и(х) > и(у) и из x~y следует и(х) = и(у). Для каждого потребителя такое представление многовариантно. Например, если и(х) - функция полезности, Сu(х), ln[u(x)] - это также индикаторы, предпочтений.

Введение функции полезности позволяет заменить отношения предпочтения привычными отношениями между числами: больше, меньше, равно.

В теории потребления предполагается, что функция полезности обладает следующими свойствами:

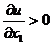1) - с ростом потребления блага полезность растет;

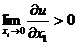2) - небольшой прирост блага при его первоначальном отсутствии резко увеличивает полезность;

3) - с ростом потребления блага скорость та полезности замедляется;

4) - при очень большом объеме блага его дальнейшее увеличение не приводит к увеличению полезности.

Условие 3 обычно используется в более расширительной трактовке: матрица вторых производных (матрица Гессе)

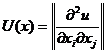
отрицательно определена.

Предельной, полезностью товараназывается предел отношения приращения полезности к вызвавшему этот прирост приращению товара:

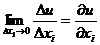
таким образом, предельная полезность показывает, насколько возрастает полезность, если товар возрастет на малую единицу.

Поверхностью безразличия называется гиперповерхность размера (n-1), на которой полезность постоянна:

или в дифференциальной форме:

, (1.18)

Условие (1.18) означает, что касательная к поверхности безразличия перпендикулярна градиенту полезности.

С точки зрения потребителя наличие множества наборов товаров, обладающих одинаковой полезностью (т.е. одинаковой степенью предпочтения), означает возможность замены одного набора другим равноценным набором, в том числе возможность замены одного товара другим.

Пусть в соотношении (1.18) dx_i = 0 для i = 3,…, n, тогда это соотношение примет вид

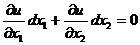откуда

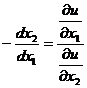(1.19)

т.е. предельная норма заменыпервого товара вторым равна отношению предельных полезностей первого и второго товаров. Норма замены показывает, сколько требуется единиц второго товара, чтобы заменить выбывшую малую единицу первого товара.

Бюджетным множеством называется множество тех наборов товаров, которые может приобрести потребитель, имея доход М:

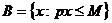где p = (p₁,…, p_n) - вектор-строка цен.

Модель поведения потребителя

В теории потребления предполагается, что потребитель стремится максимизировать свою полезность и единственное, что его сдерживает, - это ограниченность дохода:

(1.20)

В задаче (1.20) предполагается, что точка максимума 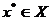. Эта задача на условный экстремум сводится к нахождению безусловного экстремума функции Лагранжа:

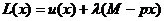Необходимые условия локального экстремума:

, (1.21)

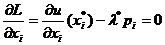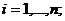, (1.22)

эти условия действительно определяют точку максимума, поскольку матрица U отрицательно определена.

Из (1.22) видно, что потребитель при фиксированном доходе так выбирает набор x*, что в этой точке отношения предельных полезностей равны отношениям цен:

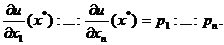
Если разрешить (1.21), (1.22) относительно х*, получим функцию спроса потребителя:

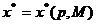. (1.23)

Уравнение Слуцкого

Рассмотрим, как изменится спрос потребителя, определяемый моделью (1.20), если изменится цена одного из товаров.

Пусть цена n-го товара возросла на dр_n, тогда согласно (1.23) спрос на каждый товар изменится следующим образом:

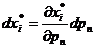, i = 1, 2,…, n,

но поскольку (1.23) - это, другая запись соотношений (1.21), (1.22), то уравнение для 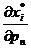получим путем дифференцирования по р_п этих соотношений:

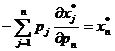, (1.24)

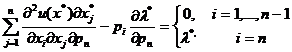Система из (n + 1) линейного уравнения (1.24) относительно (п + 1) неизвестного 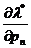, , …, 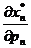в матричной форме запишется следующим образом (штрих означает транспортирование; р - вектор-строка цен; U - матрица Гессе; х^* - вектор-столбец спроса на товары):

. (1.25)

Непосредственной проверкой можно установить, что обратная матрица к матрице уравнений (1.25) имеет вид:

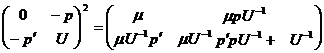где .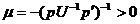

Поэтому решение уравнений (1.25) в матричной форме выглядит так:

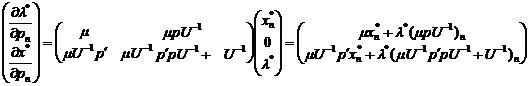Дата добавления: 2021-01-20; просмотров: 83; Мы поможем в написании вашей работы!

Поделиться с друзьями:

12 3 Следующая ⇒

Мы поможем в написании ваших работ!