Частотный метод определения потока излучения и его частотно-временного спектра на выходе подвижного транспаранта МАИ
Для этого метода требуется заранее определить ПЧС 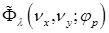 квазимонохроматического потока излучения на выходе неподвижного МАИ.
квазимонохроматического потока излучения на выходе неподвижного МАИ.
Если известен ПЧС 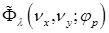 для неподвижного транспаранта МАИ, то при его движении по произвольному закону, описываемому системой параметрических уравнений
для неподвижного транспаранта МАИ, то при его движении по произвольному закону, описываемому системой параметрических уравнений
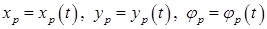 ,
,
функцию, описывающую зависимость квазимонохроматического потока от времени можно определить по формуле
 . (2.4.32)
. (2.4.32)
Рассмотрим методику определения частотно-временного спектра на выходе МАИ на примере линейного закона и кругового сканирования, а также при вращательном движении МАИ.
Линейное сканирование
Как отмечалось выше, при линейном сканировании (см. рис. 2.4.8) система параметрических уравнений имеет вид
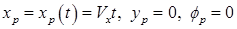 .
.
С учётом этих уравнений выражение (2.4.32) запишется как
 , (2.4.33)
, (2.4.33)
где в соответствии с формулой (2.4.5) ПЧС квазимонохроматического потока излучения на выходе МАИ определяется выражением
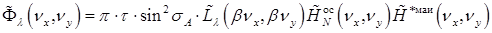 . (2.4.34)
. (2.4.34)
Чтобы получить ЧВС потока излучения, необходимо вычислить прямое преобразование Фурье от (2.4.33). Тогда
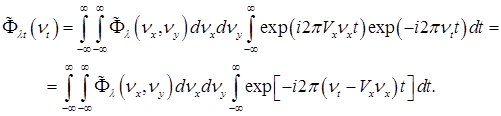 (2.4.35)
(2.4.35)
Так как
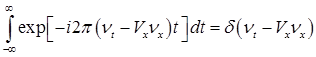 ,
,
то, учитывая фильтрующее свойство  функции, получим следующее выражение ЧВС квазимонохроматического потока на выходе МАИ
функции, получим следующее выражение ЧВС квазимонохроматического потока на выходе МАИ
 (2.4.36)
(2.4.36)
Подставив (2.4.34) в (2.4.36), получим окончательное выражение для ЧВС потока в виде
 . (2.4.37)
. (2.4.37)
Таким образом, для определения ЧВС потока излучения на выходе МАИ при линейном сканировании необходимо знать ПЧС объекта, ОПФ ОС и ППФ МАИ.
|
|
|
Круговое сканирование
При круговом сканировании система параметрических уравнений, описывающая относительное перемещение транспаранта МАИ и изображения, имеет вид
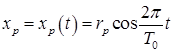 ,
,  ,
, 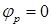 ,
,
где 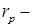 радиус кругового сканирования,
радиус кругового сканирования, 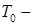 период сканирования.
период сканирования.
С учётом этих уравнений выражение (2.4.32) представляется в виде
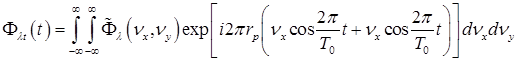 . (2.4.38)
. (2.4.38)
В соответствии с формулой (2.4.31) ЧВС при вращательном сканировании и круговом движении определяется значениями 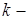 тых гармоник спектра. Гармоники при таком периодическом движении определяются коэффициентами ряда Фурье, а именно,
тых гармоник спектра. Гармоники при таком периодическом движении определяются коэффициентами ряда Фурье, а именно,
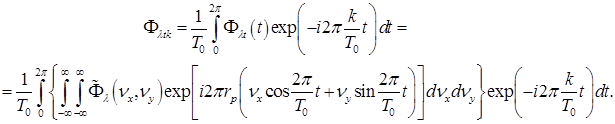 (2.4.39)
(2.4.39)
Выразим для экспоненциальной функции формулы, входящей в формулу (2.4.39), пространственные частоты в полярной системе координат. Тогда 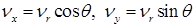 , а аргумент экспоненты в круглых скобках описывается формулой
, а аргумент экспоненты в круглых скобках описывается формулой
 . (2.4.40)
. (2.4.40)
Следовательно, выражение (2.2.39) с учётом (2.4.40) можно представить в виде
 . (2.4.41)
. (2.4.41)
Рассмотрим выражение, содержащееся в фигурных скобках формулы (2.4.41). Если в этом выражении сделать замену переменной  ,
, 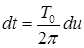 , то, учитывая периодичность подынтегральной функции, получим
, то, учитывая периодичность подынтегральной функции, получим
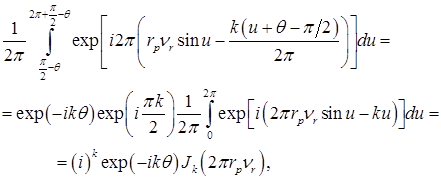 (2.4.42)
(2.4.42)
где 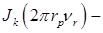 функция Бесселя 1-го рода k-го порядка.
функция Бесселя 1-го рода k-го порядка.
Так как 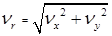 и
и  , то окончательно формулу для вычисления
, то окончательно формулу для вычисления 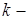 тых гармоник ЧВС можно представить выражением
тых гармоник ЧВС можно представить выражением
|
|
|
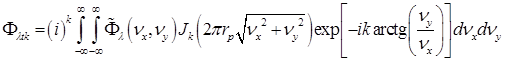 , (2.4.43)
, (2.4.43)
где  ПЧС на выходе неподвижного транспаранта МАИ, который определяется формулой (2.2.34).
ПЧС на выходе неподвижного транспаранта МАИ, который определяется формулой (2.2.34).
Вращательное движение МАИ
При вращательном движении транспарант МАИ вращается вокруг своей оси с постоянной угловой скоростью и закон движения имеет вид
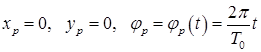 .
.
Тогда с учётом периодического закона сканирования выражение (2.4.32), описывающее зависимость квазимонохроматического потока от времени, можно определить по формуле
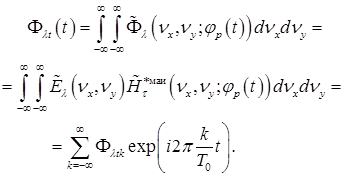 . (2.4.44)
. (2.4.44)
Представив выражение (2.4.44) в полярной системе координат, получим
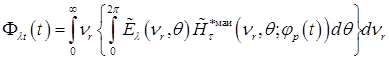 . (2.4.45)
. (2.4.45)
При повороте МАИ на угол 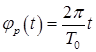 его функция пропускания в полярной системе координат представляется периодической функцией
его функция пропускания в полярной системе координат представляется периодической функцией 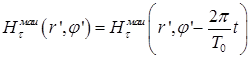 , а ППФ – периодической функцией
, а ППФ – периодической функцией  .
.
Следовательно, 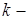 ую гармонику ЧВС потока на выходе МАИ можно определить как
ую гармонику ЧВС потока на выходе МАИ можно определить как
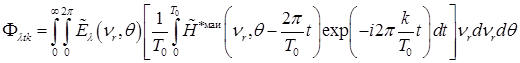 . (2.4.46)
. (2.4.46)
Введём обозначение
 , (2.4.47)
, (2.4.47)
и сделаем замену переменной 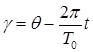 ,
,  . Тогда
. Тогда
 (2.4.48)
(2.4.48)
Так как  является периодической функция с периодом
является периодической функция с периодом  по углу
по углу  , то разложим её в ряд Фурье
, то разложим её в ряд Фурье
 , (2.4.49)
, (2.4.49)
где
 . (2.4.50)
. (2.4.50)
Для 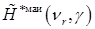 получаем
получаем
 . (2.4.51)
. (2.4.51)
Подставив (2.4.51) в (2.4.48), получим
 . (2.4.52)
. (2.4.52)
Применив свойство ортонормированности к интегралу в выражении (2.4.52), получим следующий результат
|
|
|
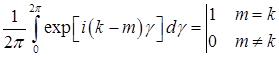 .
.
Тогда
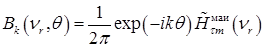 . (2.4.53)
. (2.4.53)
При вращении транспаранта МАИ функцию 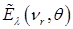 можно рассматривать как периодическую с периодом, равным
можно рассматривать как периодическую с периодом, равным  . Выполнив аналогичные преобразования для
. Выполнив аналогичные преобразования для 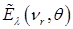 , получим
, получим
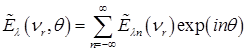 , (2.4.54)
, (2.4.54)
где
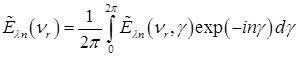 . (2.4.55)
. (2.4.55)
Подставив (2.4.53) и (2.4.54) в выражение (2.4.46) и использовав свойство ортонормированности
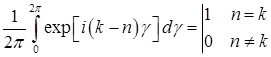 ,
,
получим следующую формулу для 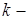 ой гармоники ЧВС потока при вращательном движении МАИ
ой гармоники ЧВС потока при вращательном движении МАИ
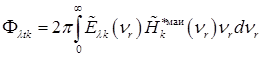 , (2.4.56)
, (2.4.56)
где
 , (2.4.57)
, (2.4.57)
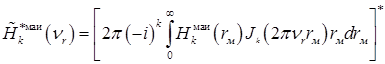 , (2.4.58)
, (2.4.58)
 . (2.4.59)
. (2.4.59)
Дата добавления: 2021-01-20; просмотров: 75; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
