Программный комплекс « Алгоритмы факторизации»
Функциональное назначение программы, область применения, её ограничения
Программный комплекс предназначен для реализации алгоритмов факторизации.
Результатом работы данного решения является разложение натурального числа в произведение простых чисел, на основе алгоритмов факторизации.
Ограничения применения программного комплекса определяются произ-водительностью персонального компьютера (ПК).
Программа разработана на языке программирования python версии 3.8.
Программный комплекс предназначен для работы на ПК с системами Windows 7 с пакетом обновления 1 (SP1) (с последними обнов-лениями Windows) и выше.
Для корректной работы программного комплекса необходимо наличие ПК с процессором с тактовой частотой не ниже 1,8 ГГц. Рекомендуется как минимум двухъядерный процессор. Необходимый объем оперативной памяти составляет 1 ГБ ОЗУ. Рекомендуется 2 ГБ ОЗУ (минимум 2,5 ГБ при выполнении на виртуальной машине). Место на жестком диске: минимум 100 МБ свободного места.
Проведенные эксперименты показывают, что для работы с данным про-граммный комплексам не требуется специальной подготовки, она интуитивно понятна и осваивается за несколько минут от начала работы с данной программой. В пунктах 2.2 и 2.3 представлены руководства программиста и пользователя.
Руководство программиста
Программное обеспечение включает в себя основное окно с кодом через которое осуществляется управление и доступ к отдельным методам.
|
|
|
Данное программное обеспечение использует следующие библиотеки:
- sys;
- match;
Matchодин из наиважнейших в Python. Этот модуль предоставляет обширный функционал для работы с числами. [10].
Основной код программы находится в классе GetLehmanFactor. Функции этого класса вызывают функции других классов.
Функция Trunc возвращает целочисленную часть числа с плавающей запятой.Она возвращает эту часть как Целочисленное значение.
Функция Sqrt возвращает квадратный корень числа (Number).Число должно быть вещественного типа.[11]
Функция Power возводит X в степень Y. Значение аргумента Х должно быть больше нуля, иначе возникнет исключение EInvalidOp. Данная функция аналогична функции IntPower за исключением того, что для Power значение показателя степени Y может превышать MaxInt и иметь нецелочисленный тип.
Процедура Assert используется в Delphi при отладке программы на предмет истинности утверждений. Эти утверждения по смыслу должны быть истинны, но почему-то могут нарушаться. Если проверяемое утверждение будет ложным, то процедура прекратит работу и сгенерирует исключение EAssertionFailed с выдачей ошибки в сообщении.
Функции ceil возвращают значение с плавающей запятой, представляющее наименьшее целое число, которое больше или равно x. Ошибки не возвращаются.[12]
|
|
|
Программа разработана на языке программирования python версии 3.8 и имеет стандартный интерфейс. Для работы ПО не нужно наличие каких-либо дополнительных программно-аппаратных средств.
Первое окно программы – главное меню, является точкой доступа ко всем функциям программы.
Второе окно- разложение натурального числа по алгоритму Ферма.
На вход функции подаются: натуральное число; специальная переменная k, которая будет использоваться в вычислениях и переменная, которая при достижении определённого значения закончит алгоритм.
Блок - схема алгоритма вычисление с использованием алгоритма Ферма представлена на рисунке 1.
| Конец |
| Начало |
| Вводим n |
| Проверяем n на нечётность |
| Находим S1 и S |
| Если S не равен S1 |
| a=s, print(n,’=’,a,’*’,a) |
| X=S+K |
| L=x2-n |
| Y1=sqrt(L),y |
| Если y==y1 |
| K+=1 |
| A=x+y, B=x-y |
| Print(n=a*b) |
| Если a==1 or b==1 |
| Print(n-простое число), z=0 |
| Да |
| Да |
| Да |
| Да |
| Нет |
| Нет |
| Нет |
| Нет |
Рисунок 1 – Блок-схема вычисления с использованием алгоритма Ферма
|
|
|
На выходе ответ будет представлен в виде: (Число n, и его множители)
Третье окно – разложение натурального числа по алгоритму Лемана.
Для вычисления используется функцияGetLehmanFactor. На вход функции подаётся натурального число, которое будет использоваться в вычислениях
Блок-схема алгоритма вычисления по алгоритму Лемана представлена на рисунке 2
| Начало |
| Конец |
| Вводим N |
| Находим все a до N1/3 |
| Если N/a: |
| Находим k и d |
| Находим F |
| Вычисляем A и B |
| Находим НОДd1= (A-B;N) |
| Вычисляем второй множительd2=N/d1 |
| Print(N, ’=’, d1,’*’,d2) |
| Print(N, ’=’, a,’*’, b) |
Рисунок 2 – блок-схема вычисления по алгоритму Лемана
На выходе функции выводится два множителя.
Руководство пользователя
Программ имеет одно основное окно, через которое происходит управление функциями.

Рисунок 3- Окно программы
Разложение по алгоритму Ферма происходит при вводе в программу единицы. После чего выйдет новая подсказка, которая предложит ввести число. Ввод данных при алгоритме Ферма изображён на рисунке 4.

Рисунок 4 – Ввод данных при алгоритме Ферма
Вводим натуральное число и нажимаем на кнопку, чтобы ввести данное в программу. Дальше нам выйдет результат. Результат разложения по алгоритму Ферма изображён на рисунке 5.
|
|
|

Рисунок 5 – Результат разложения по алгоритму Ферма
Для того чтобы воспользоваться алгоритмом Лемана, возвращаемся к начальной подсказке где нас просят ввести 2 если хотим использовать этот алгоритм. После ввода двойки выходит новая подсказка, где нас просят ввести число. Ввод данных при алгоритме Лемана изображён на рисунке 6.

Рисунок 6 – Ввод данных при алгоритме Лемана
Вводим натуральное число и нажимаем на кнопку, чтобы ввести данное в программу. Дальше нам выйдет результат. Результат разложения по алгоритму Лемана изображён на рисунке 7.

Рисунок 7 – Результат разложения по алгоритму Лемана
Тестовый пример
Реализуем алгоритм Ферма
Для примера возьмём большое число n=89755.
1)Найдём корень от числа n. 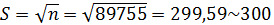
2)Если значение получилось не целое, ищем 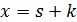 , x=300+0=300
, x=300+0=300
3)Находим переменную 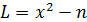 , L=3002-89755=245
, L=3002-89755=245
4)Находим Y1. 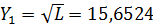
5) Округляем значение y1 и присваиваем полученное значение y.Y=16
6) Если Y1 не равен Y, то прибавляем 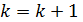 и повторяем шаг 2, до тех пока они не станут равны. K=82, L=3822-89755=56169, Y1=237, Y1=Y
и повторяем шаг 2, до тех пока они не станут равны. K=82, L=3822-89755=56169, Y1=237, Y1=Y
7)Находимaиb. 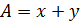 ,
, 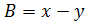 . A=382+237=619, B=382-237=145
. A=382+237=619, B=382-237=145
8)Данное разложение является не конечным, так как, очевидно, что число 145 не является простым: 145=29*5
В итоге, конечное разложение исходного числа {\displaystyle n}n на произведение простых множителей 89755=29*5*619
Разложение получено, теперь посмотрим, какой результат даст программа.
Результат разложения показан на рисунке 8.

Рисунок 8 – Результат разложения
Программа показала правильный ответ.
Реализуем алгоритм Лемана.
1)Разберем пример с n=1387, тогда для  , где
, где 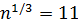 , проверяем является ли число a делителем числа n. Не трудно убедится, что таких нет, тогда переходим к следующему пункту.
, проверяем является ли число a делителем числа n. Не трудно убедится, что таких нет, тогда переходим к следующему пункту.
2) Для всех 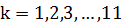 и всех
и всех 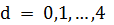 проверяем, является ли число
проверяем, является ли число 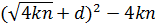 квадратом натурального числа. В нашем случае существуют такие k=3 и d=1, что выражение
квадратом натурального числа. В нашем случае существуют такие k=3 и d=1, что выражение 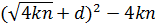 является полным квадратом и равно 256=162.
является полным квадратом и равно 256=162.
3)Находим A и B по формуле  и
и 
A=130 и B=16.
4)Тогда находим наибольший общий делитель 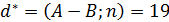 , удовлетворяет неравенству
, удовлетворяет неравенству 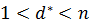 и является делителем числа n. В итоге, мы разложили число 1387 на два множителя: 73 и 19.
и является делителем числа n. В итоге, мы разложили число 1387 на два множителя: 73 и 19.
Разложение получено, теперь посмотрим, какой результат даст программа.
Результат разложения показан на рисунке 9.

Рисунок 9 – Результат разложения
Программа показала правильный ответ.
Заключение
В ходе выполнения курсовой работы было произведено ознакомление с алгоритмами факторизации. Были реализованы в виде программы 2 алгоритма факторизации: Метод Ферма, метод Лемана. Была проведена проверка программы, в результате которой, было выявлено, что программа успешно справляется со своей задачей.
Дата добавления: 2021-01-20; просмотров: 145; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
