Предельная скорость движения газа. Число Маха

Стр 1 из 4Следующая ⇒

Лекция 2. УРАВНЕНИЯ ГАЗОВОЙ ДИНАМИКИ ДЛЯ ЕДИНИЧНОЙ СТРУЙКИ (4 часа)

План:

2.1. Уравнение неразрывности

2.2. Уравнение энергии

2.2. Предельная скорость движения газа. Число Маха.

2.4. Механическая форма уравнения энергии (уравнение Бернулли)

2.5. Уравнение количества движения

2.6. Расчет реактивной силы (тяги) (*)

Уравнение неразрывности

Выведем основные уравнения газовой динамики для элементарной струйки газа, поперечные размеры которой настолько малы, что в каждом ее сечении можно считать постоянными все основные параметры потока: скорость, давление, температуру и плотность газа. Именно в таком виде уравнения газовой динамики применяются обычно в теории ДВС.

Чтобы получить уравнение неразрывности, рассмотрим стационарное (установившееся) движение элементарной струйки газа (рис. 2.1). При стационарном движении в любой точке пространства сохраняются неизменными по времени скорость движения и состояние жидкости (плотность, давление, температура).

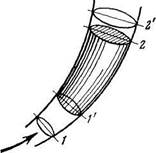
Рис. 2.1. Элементарная струйка

Рассмотрим некоторый участок струйки между двумя нормальными к поверхности тока сечениями 1 и 2; заметим, что в объеме 1—2 приток газа осуществляется только через поперечное сечение 1, а расход газа — только через сечение 2.

За бесконечно малый промежуток времени dτ выделенная часть струйки переместится в новое положение 1’ — 2'. Перемещение состоит в том, что за время dτ заштрихованный объем 1'-2 вместит газ, вытесненный из области 1 — 1', аизвестное количество газа за то же время вытечет из этого объема и заполнит область 2 — 2'. Приток газа в объем 1' — 2 составляет

(2.1.)

где ρ₁ — плотность газа в поперечном сечении 1, F ₁ — площадь поперечного сечения 1. Расстояние между сечениями 1 и 1’ равно произведению скорости движения на элементарный промежуток времени:

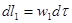
где w ₁ — скорость в сечении 1, откуда

Расход газа из объема 1’ — 2 равен,, очевидно

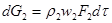
При установившемся режиме и отсутствии разрывов сплошности в движущейся среде приток газа должен равняться расходу:

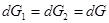
Отсюда после соответствующей подстановки получаем уравнение неразрывности — закон сохранения массы — для единичной струйки сжимаемой жидкости (газа) при установившемся течении

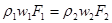или r wF = const (2.2)

В случае несжимаемой жидкости, т. е. при r = const, уравнение (2.2) принимает более простую форму:

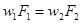(2.3)

которая применима к газовым течениям в тех случаях, когда изменениями плотности газа можно пренебречь.

На основании уравнения (2.3) по расположению линий тока в несжимаемой среде можно судить о скорости движения. В местах сгущения линий тока скорость растет; если линии тока раздвигаются, то скорость падает.

В газе, как нетрудно видеть из уравнения неразрывности (2.2), картина линий тока однозначно определяет изменение плотности тока:

представляющей произведение плотности газа на скорость, т. е. массовый расход газа через единицу площади поперечного сечения.

В местах сгущения линий тока плотность тока увеличивается, а в местах расхождения линий тока — убывает.

Уравнение постоянства расхода газа G = pwF = const можно представить также в дифференциальной форме

Поделив почленно это соотношение на pwF , получим:

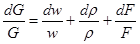(2.4)

Уравнение энергии

Следуя первому началу термодинамики (закону сохранения энергии), составим баланс энергии в неподвижной системе координат (рис. 2.1), т.е. рассмотрим преобразование энергии в одной и той же массе газа, заполнявшей вначале объем 1 — 2, а через бесконечно малый промежуток времени dτ переместившейся в положение 1' — 2'.

Приращение любого вида энергии равно разности количеств этого вида энергии в положениях 1’ — 2' и 1 — 2. Ввиду того, что заштрихованный объем 1’ — 2 является общим для этих двух положений, приращение энергии измеряется разностью количеств энергии в бесконечно малых объемах 2 — 2' и. 1 — 1'. Отсюда следует, что приращение кинетической энергии равно

(2.5)

здесь dG — массовый расход газа через поперечное сечение струйки за время dτ . Приращение потенциальной энергии (энергии положения)

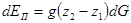(2.6)

где z ₂ и z₁ — высоты расположения (нивелирные уровни) сечений 2 и 1, g — ускорение силы тяжести. Приращение внутренней (тепловой) энергии

(2.7)

где U = c_v - T — тепловая энергия единицы массы газа (произведение теплоемкости при постоянном объеме на абсолютную температуру). Если теплоемкость газа в сечениях 1 и 2 одинакова, то прирост внутренней энергии равен

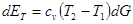(2.8)

На основания выделенной части струйки газа действуют направленные внутрь и по нормали к ним внешние силы давления р. При перемещении газа внешние силы давления производят работу. Например, перенос газа из сечения 1 в сечение 1’ происходит как бы под действием поршня площадью F ₁ с давлением р₁. Работа поршня за время dτ равна

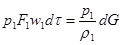(2.9)

Точно так же можно представить себе, что давление р₂ на сечение 2 осуществляется поршнем площадью F _2. За время d τ газ переместит поршень в положение 2, производя отрицательную работу

Силы давления, действующие на боковую поверхность струйки (поверхность тока), никакой работы не производят, так как они нормальны к траекториям движения частиц газа. Таким образом, энергия, внесенная силами давления, равна разности между работами поршня 1 и поршня 2:

(2.10)

К газовой струйке на участке 1 — 2 может быть за время dt подведено тепло в количестве . Далее газовая струйка за время d τ может произвести техническую работу dl , например, приводя во вращение колесо турбины, установленное между сечениями 1 и 2. Наконец, следует учесть энергию, расходуемую газом за время d τ на преодоление сил трения dl_Tp.

Согласно первому началу термодинамики подведенные к газу тепловая энергия и работа сил давления расходуются на совершение технической работы, работы сил трения, а также на изменение внутренней энергии

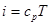(2.11)

Тогда соотношение (2.11) примет несколько иной вид:

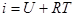(2.12)

или на основании (2.10)

(2.13)

Используя выражения (2.6), (2.7) и (2.13), можно придать уравнению энергии следующую форму:

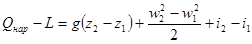(2.14)

Уравнение энергии (2.14) иногда называют также уравнением теплосодержания. Существенно то обстоятельство, что уравнение теплосодержания не содержит работы трения. Поскольку энергия, расходуемая на преодоление трения или любого другого вида сопротивлений, преобразуется полностью в тепло, а последнее остается в газовой струе, наличие сил трения не может нарушить общий баланс энергии, а лишь приводит к преобразованию одного вида энергии в другой.

Обычно в технике приходится иметь дело с частными формами уравнения теплосодержания. Так, в большинстве случаев изменение потенциальной энергии пренебрежимо мало в сравнении с другими частями уравнения энергии, и членом g ( z ₂ — z₁) пренебрегают. Тогда уравнение теплосодержания имеет следующий вид:

(2.15)

При отсутствии технической работы и теплообмена с окружающей средой, т. е. в случае энергетически изолированного процесса в газе, имеем

(2.16)

В частности, уравнение (2.16) определяет движение газа по трубе, если нет теплопередачи через стенки. Согласно сказанному это уравнение справедливо вне зависимости от того, действуют или нет силы трения. Иначе говоря, изменение теплосодержания (температуры) в энергетически изолированном процессе связано только с изменением скорости. Если скорость газа не меняется, то остается постоянной и температура.

Если нет теплообмена, но присутствует техническая работа, то расчет лишь немного усложнится. Именно:

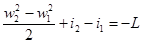(2.17)

Когда технической работы нет, уравнение теплосодержания дает

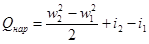(2.18)

в таком виде оно применяется к теплообменным процессам.

Применительно к энергетически изолированным течениям газа, когда выполняются условия

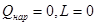(2.19)

и уравнение теплосодержания приобретает форму (2.16). Его можно записать следующим образом

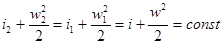(2.20)

Отсюда нетрудно видеть, что если газовую струю затормозить полностью, то теплосодержание газа достигает максимального возможного значения:

(2.21)

Получающееся при этом значение теплосодержания i * называется полным теплосодержанием, а соответствующую абсолютная температура

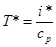(2.22)

— температурой торможения.

Итак, температура газа получается равной температуре торможения в том случае, когда скорость течения уменьшается до нуля при отсутствии энергетического обмена с окружающей средой. Пользуясь средним значением теплоемкости, можно вычислить температуру торможения по следующей формуле:

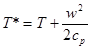(2.23)

Следует подчеркнуть, что, согласно уравнению энергии (2.20), в энергетически изолированном потоке идеального газа существует однозначная зависимость между температурой газа Т (теплосодержанием i ) и скоростью течения w. Повышение скорости в таком потоке всегда сопровождается снижением температуры независимо от изменения других параметров газа.

Предельная скорость движения газа. Число Маха

Рассматривая истечение газа при отсутствии энергетического обмена, можно убедиться в том, что скорость истечения ни при каких условиях не может быть выше некоторой максимальной величины. Из соотношения

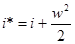
следует, что максимальная скорость достигается в том случае, когда теплосодержание в потоке равно нулю, т.е. когда полное теплосодержание газа целиком преобразуется в кинетическую энергию

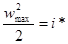
Отсюда получим формулу для максимального значения скорости в газе

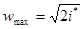(2.24)

Для того чтобы перевести газ из состояния покоя в движение со скоростью w , необходимо израсходовать часть его теплосодержания, равную

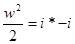
Разделив обе части этого равенства на полное теплосодержание, получим

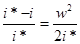
При постоянной теплоемкости это безразмерное выражение примет следующий вид:

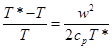
Если теперь умножить и разделить правую часть на газовую постоянную R , учесть соотношение R = с_р — с_v и обозначить отношение теплоемкостёй через k = c_p / c_v , то получится

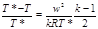
Но, как известно из физики, скорость звука в газе равна:

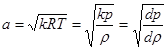(2.25)

Поэтому степень использования теплосодержания газа для получения заданного значения скорости потока определяется отношением скорости потока к скорости звука в неподвижном газе:

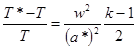
Отсюда выводится новое выражение для максимальной скорости истечения (T = 0):

(2.26)

Можно тепловой перепад разделить не на полное теплосодержание, а на теплосодержа-ние в потоке; тогда получим

В этом случае скорость потока оказывается отнесенной к скорости звука в потоке, а не в неподвижном газе:

(2.27)

Отношение скорости потока к скорости звука в потоке принято называть числом Маха и обозначать буквой М:

(2.28)

Число Маха характеризует степень преобразования теплосодержания в кинетическую энергию потока

Число Маха является основным критерием подобия для газовых течений большой скорости.

Если M< 1, то течение газа называется дозвуковым, при М > 1 — сверхзвуковым.

Из последнего выражения можно получить расчетную формулу для отношения температуры торможения к температуре в потоке как функцию числа Маха:

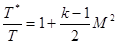(2.29)

Поскольку скорость потока может быть как выше, так и ниже скорости звука, существует и такой режим, когда скорость потока равна скорости звука, т.е. М= 1. Этот режим называется критическим; ему соответствует значение температуры в потоке:

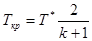(2.30)

Можно характеризовать степень преобразования теплосодержания в кинетическую энергию еще одним способом, поделив тепловой перепад на теплосодержание при критическом режиме:

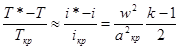(2.31)

Отсюда с помощью равенства (2.25) получаем новую формулу для отношения температур в энергетически изолированном газовом течении:

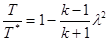(2.32)

Эту величину, измеряющую отношение скорости потока к критической скорости , принято обозначать

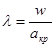(2.33)

и называть приведенной скоростью. На критическом режиме ( w = w _кр = а_кр) приведенная скорость λ_кр = М_кр = 1. Максимальной скорости потока при Т = 0 соответствует определенное максимальное значение приведенной скорости

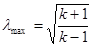(2.34)

Приведенная скорость, как и число М, может считаться критерием подобия для газовых течений, характеризующим степень преобразования теплосодержания в кинетическую энергию.

Данному значению числа М соответствует совершенно определенное значение приведенной скорости.

Формулу перехода от числа М к приведенной скорости выглядит следующим образом:

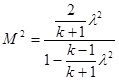(2.35)

или

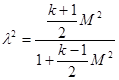(2.36)

Дата добавления: 2020-12-12; просмотров: 153; Мы поможем в написании вашей работы!

Поделиться с друзьями:

12 3 4 Следующая ⇒

Мы поможем в написании ваших работ!