Деление отрезков прямых на равные части.
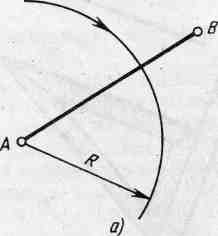
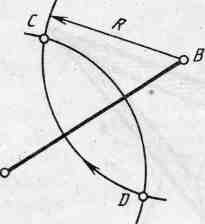
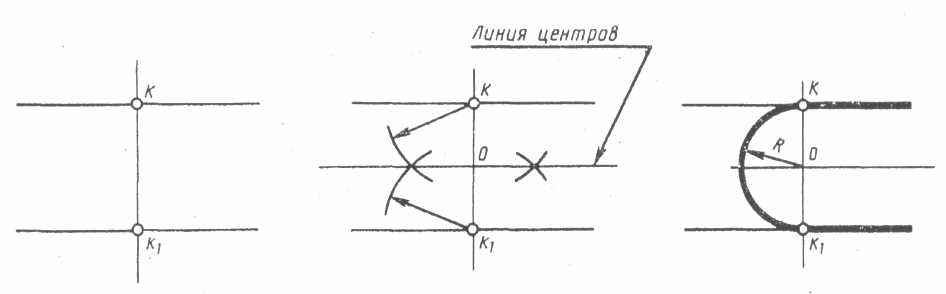
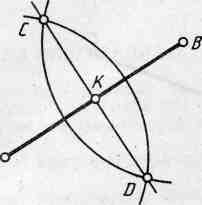Чтобы разделить отрезок пополам нужно из концов отрезка циркулем провести две дуги окружности радиусом R, несколько большем половины данного отрезка, до взаимного пересечения. Полученные точки Д и С соединяют прямой, которая делит отрезок АВ в точке К пополам. Прямая СД перпендикулярна отрезку АВ и проходит через середину.
|
|
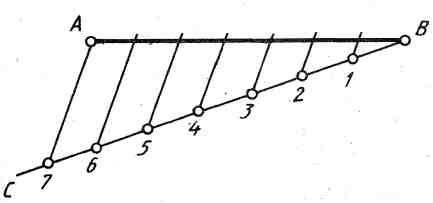Если отрезок, например отрезок АВ, необходимо разделить на несколько равных частей, то из любого конца заданного отрезка под произвольным острым углом проводят вспомогательную прямую ВС. От вершины образовавшегося угла (в данном случае от точки В) на вспомогательной прямой откладывают столько одинаковых отрезков произвольной длины, на сколько частей требуется разделить отрезок АВ. Конец последнего отрезка соединяют прямой линией с точкой А и параллельно этой линии через все деления проводят прямые до пересечения с прямой АВ, деля ее тем самым на заданное число равных отрезков.
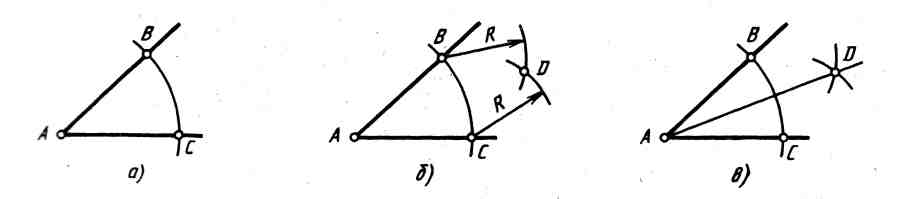Деление углов на равные части
|
|
Из вершины А заданного угла ВАС произвольным радиусом R проводят дугу до пересечения со сторонами угла в точках В и С. Из точек В и С проводят две дуги радиусом больше половины расстояния ВС до их пересечения в точке Д. Соединив точки А и Д прямой, получают биссектрису угла, которая делит угол пополам.
Деление окружности на равные части и построение правильных вписанных многоугольников
|
|
|
Деление окружности на четыре равные частии построение правильного вписанного четырёхугольника.
Две взаимно перпендикулярные центровые линии делят окружность на четыре равные части. Соединив точки пересечения этих линий с окружностью, получают правильный вписанный четырёхугольник. Разделив два прямых угла пополам, соединяют полученные точки на поверхности окружности. Получают правильный вписанный четырехугольник.
Деление окружности на восемь равных частейи построение правильного восьмиугольника. Две взаимно перпендикулярные линии, проведённые под углом 45° к центровым линиям с помощью циркуля или угольника с углами 45°, делят окружность на восемь равных частей, которые соединяют последовательно прямыми линиями.
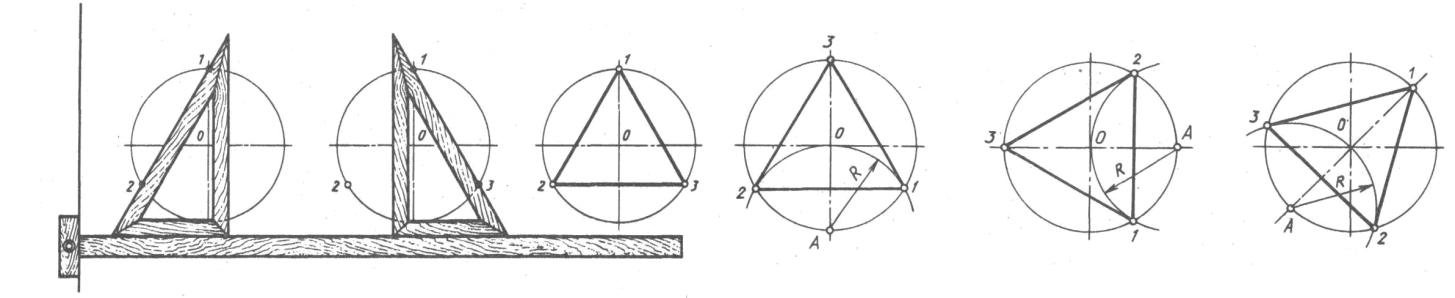
Деление окружности на три равные части и построение правильного вписанного треугольника выполняют с помощью циркуля. Из любой точки окружности проводят дугу, радиусом R, равным радиусу окружности, точки пересечения радиуса и окружности соединяют прямыми линиями. Третья точка будет находиться на противоположном конце диаметра.
При делении окружности на шесть равных частей циркулем из двух концов одного диаметра радиусом, равным радиусу данной окружности, проводят дуги до пересечения с окружностью в т. 2, 6, 3, 5. Последовательно соединив полученные точки, получают правильный вписанный шестиугольник.
|
|
|
Деление окружности на двенадцать равных частейи построение правильного вписанного двенадцати- угольника выполняют с помощью угольника с углами 30°, 60° и 90° и линейки или циркуля. При делении окружности циркулем из четырёх концов взаимно перпендикулярных диаметров окружности проводят радиусом, равным радиусу данной окружности, дуги до пересечения с окружностью, соединив полученные точки, получают двенадцати угольник.
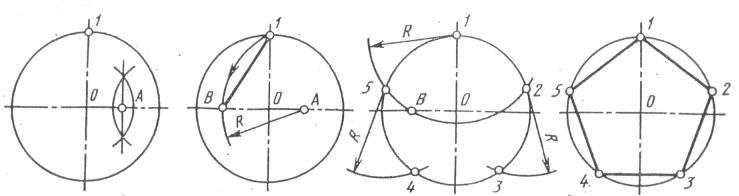Деление окружности на пять частей и построение правильного вписанного пятиугольника.
Половину любого диаметра (радиус) делят пополам, получают точку А. Из точки А, как из центра, проводят дугу радиусом, равным расстоянию от точки А до точки 1, до пересечения со второй половиной этого диаметра, в точке В. Отрезок 1В равен хорде, стягивающей дугу, длина которой равна '/5 длины окружности. Делая засечки на окружности радиусом R, равным отрезку 1В, делят окружность на пять равных частей. Начальную точку 1 выбирают в зависимости от расположения пятиугольника. Из точки 1 строят точки 2 и 5, затем из точки 2 строят точку 3, а из точки 5 строят точку 4. Расстояние от точки 3 до точки 4 проверяют циркулем; если расстояние между точками 3 и 4 равно отрезку 1B, то построения были выполнены точно.
|
|
|
Деление окружности на десять равных частейвыполняют аналогично делению окружности на пять равных частей, но сначала делят окружность на пять равных частей, начиная построение из точки 1, а затем из точки 6, находящейся на противоположном конце диаметра. Соединив последовательно все точки, получают правильный вписанный десятиугольник.
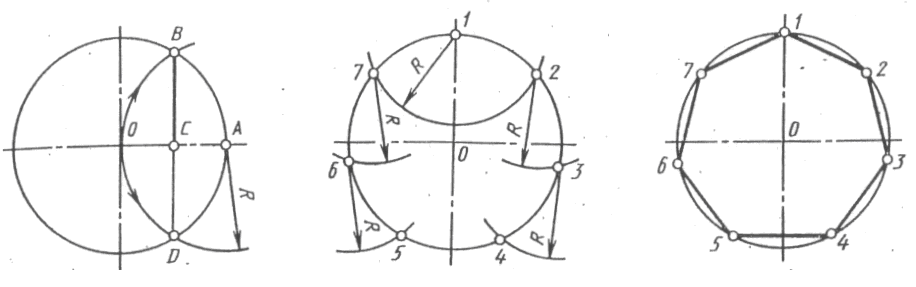
Деление окружности на семь частей и построение правильного вписанного семиугольника угольника.
Из любой точки окружности проводят дугу до пересечения с окружностью в точках В и D. Соединяют точки В и D прямой. Половина полученного отрезка (в данном случае отрезок ВС) будет равна хорде, которая стягивает дугу, составляющую 1/7 длины окружности. Радиусом, равным отрезку ВС, делают засечки на окружности в одну и другую сторону . Соединив последовательно все точки, получают правильный вписанный семиугольник . Деление окружности на четырнадцать равных частей выполняют делением окружности на семь равных частей два раза от двух точек.
|
|
|
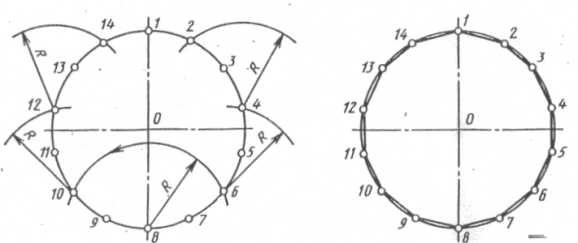Сначала окружность делится на семь равных частей от точки 1, затем тоже построение выполняется от точки 8. Построенные точки соединяют последовательно прямыми линиями и получают правильный вписанный четырнадцатиугольник. Разделить окружность на равные части можно по формуле l = kd ,где l ‑ длина хорды, k ‑ коэффициент,зависящий от числа деления окружности n , d ‑ диаметр окружности.
Разделить окружность на указанное число частей, вписать правильные многоугольники:
треугольник пятиугольник
шестиугольник семиугольник четырехугольник
четырнадцатиугольник десятиугольник
Разделить отрезок на 5 равных частей Разделить угол на 2 равные части
Сопряжение
Сопряжение – плавный переход одной линии в другую. Используют для придания деталям повышенной прочности, более красивого внешнего вида и безопасности.
Элементы сопряжения:
центр сопряжения, точки сопряжения, дуга сопряжения
Алгоритм построения сопряжений
| Сопрягаемые элементы | Центр сопряжения | Точки сопряжения | Дуга заданного радиуса | ||
| R |
центров | ||||
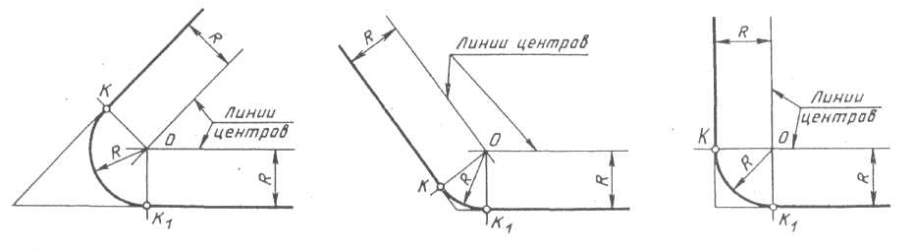
| Найти точку O – центр сопряжения, который должен лежать на расстоянии R от сторон угла, т.е. в точке пересечения прямых, проходящих параллельно сторонам угла на расстоянии R от них. | Найти точки сопряжений. Для этого из точки O опустить перпендикуляры на заданные прямые. | Из точки O, как из центра, описать дугу заданного радиуса R между точками сопряжений. | |||
|
| 
|
| |||
|
‘
| |||||
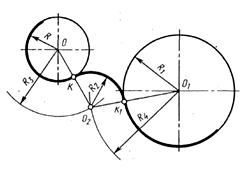
Внешнее сопряжение двух заданных окружностейдугой заданного радиуса. Если обе сопрягаемые окружности располагаются снаружи сопрягающей дуги, то центр этой дуги будет находиться от заданных окружностей на расстоянии, равном сумме радиусов (дуги и соответствующей окружности). Точки сопряжения находятся на прямых, соединяющих центр сопряжения и центры окружностей.
| Сопрягаемые элементы | Центр сопряжения | Точки сопряжения |
|  
|
|
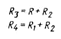
| Дуга заданного радиуса | ||
| | ||
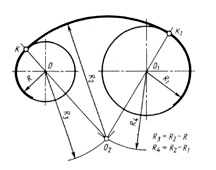
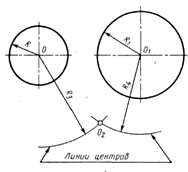
Внутренне сопряжение двух окружностей дугой заданного радиуса.Сопрягаемые окружности располагаются внутри сопрягающей дуги, и центр сопрягающей дуги будет находиться от центров заданных окружностей на расстоянии, равном разности радиусов (дуги и соответствующей окружности).
| Сопрягаемые элементы | Центр сопряжения | Точки сопряжения |
|
| 
|
|
| Дуга заданного радиуса | ||
|
| ||
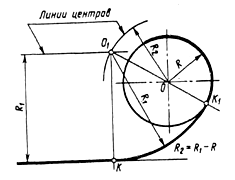
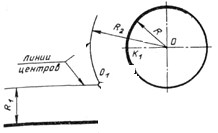
Смешанное сопряжение двух окружностей дугой заданного радиуса.В этом случае дуга сопряжения с одной окружностью имеет внешнее касание, а с другой - внутреннее.
| Сопрягаемые элементы | Центр сопряжения | Точки сопряжения | |||||||
|
| | 
| |||||||
| Дуга заданного радиуса | |||||||||
|
| |||||||||
| Внутреннее сопряжение | |||||||||
| Сопрягаемые элементы | Центр сопряжения | Точки сопряжения | |||||||
|
|
| |||||||
| Дуга заданного радиуса | |||||||||
|
| |||||||||
Вопросы для закрепления материал а :
1. Сопряжением называется...
а) излом прямой линии,
б) переход прямой линии в кривую,
в) плавный переход одной линии в другую.
2. Точкой сопряжения называется точка...
а) из которой проводят сопрягающую дугу,
б) в которой сопрягающая дуга переходит в прямую линию или сопрягаемую окружность,
в) пересечения двух вспомогательных прямых.
3.Чтобы построить центр сопряжения двух прямых, нужно провести вспомогательные прямые, параллельные данным, на расстоянии ___________________________________
4.Для построения точек сопряжения нужно из центра сопряжения _____________
___________________ к сопрягаемым прямым.
5.Расстояние от центра сопряжения до точек сопряжения равно______________
сопряжения.
6.Сопрягающая дуга - это часть окружности заданного радиуса, заключенная между .
_________________________________________________________________--
| в) |
| б) |
| а) |
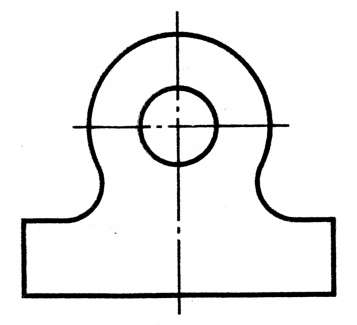
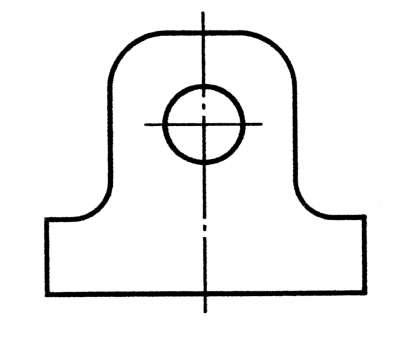7.Определить, какие элементы сопрягаются дугами окружностей. Написать названия элементов под изображениями прямых.
_________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Выполнить сопряжения прямых линий, согласно чертежей (рисунок А и В):
| А |
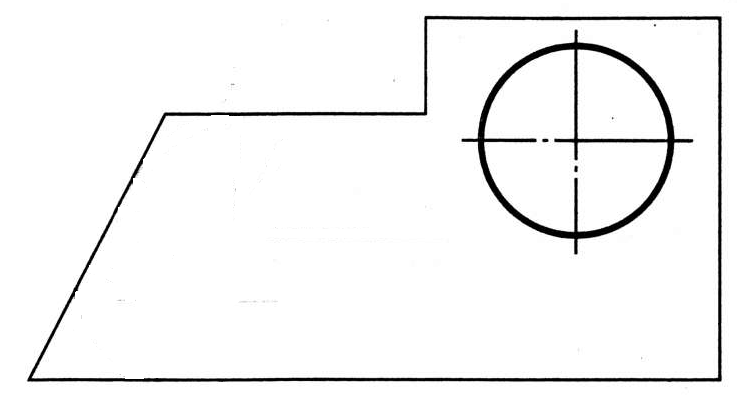
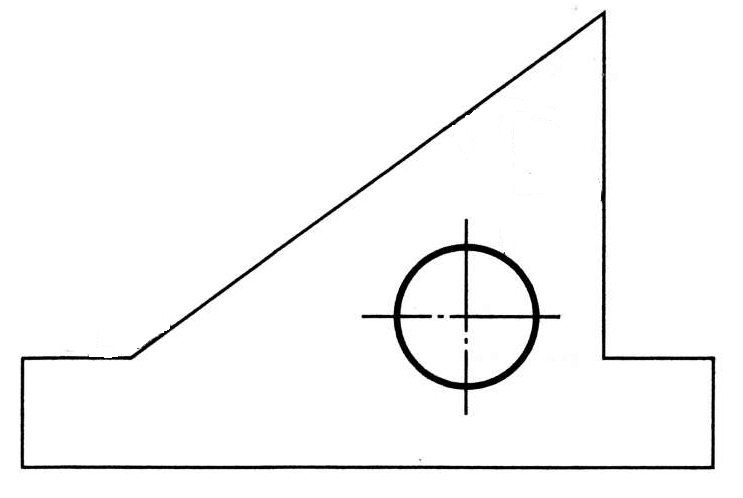
В
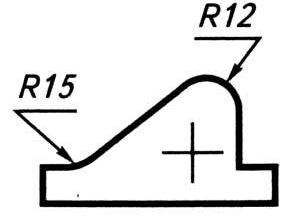
Выполнить внутреннее сопряжение окружностей
R1=20мм R2=15мм R=60мм
| R1 |
| R2 |
Выполнить внешнее сопряжение окружностей
R1=20мм R2=15мм R=15мм
| R1 |
| R2 |
Лекальные кривые
Лекальные кривые выполняют по определенным законам и обводят с помощью лекал.
Эллипс – замкнутая плоская кривая, сумма расстояний от любой точки которой до двух данных точек (фокусов) всегда равна длине большой оси эллипса.
Алгоритм выполнения
| С А В Д | ||
|
1.Разделить окружность на 12 равных частей. 2.Выполнить лучи через полученные точки. 3.Через точки, полученные на малой окружности выполнить горизонтальные линии. 4. Через точки, полученные на большой окружности выполнить вертикальные линии до пересечения с горизонтальными линиями. 5.Полученные точки будут точками эллипса. | ||
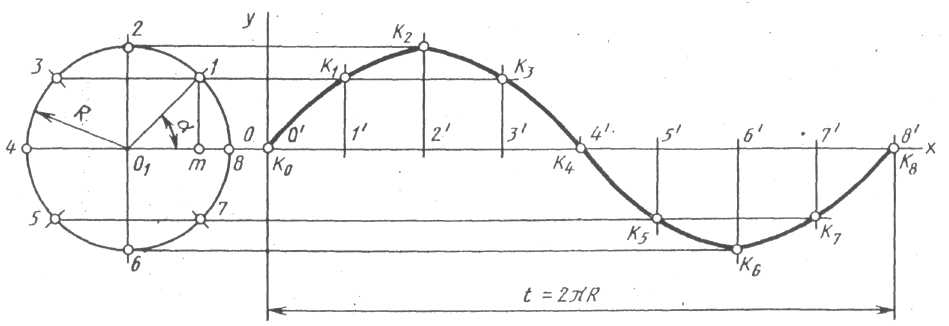Синусоида – плоская кривая, изображающая изменения синуса в зависимости от изменения его аргумента – угла α. При построении синусоиды данную окружность делят на произвольное количество равных частей. На продолжении горизонтального диаметра окружности по оси х откладывают отрезок К0К8=2πR, разделив его на то же количество равных частей. Через точки деления окружности необходимо провести ряд прямых, параллельных К0К8; из точек деления прямой К0К8 – ряд прямых, перпендикулярных К0К8. Точки пересечения одноименных вспомогательных прямых и принадлежат синусоиде.
Парабола - это плоская кривая, каждая точка которой удалена на одинаковое расстояние от заданной точки F (фокус) и заданной прямой АВ (директриса). Парабола имеет одну ось симметрии.
Алгоритм выполнения.
А
|
|
| ||||||||||
|
Вариант А
F-фокус, прямая К –директриса, точка О- вершина параболы, находится на середине расстояния от директрисы до фокуса. Через точки, взятые на оси параболы, проводят прямые, параллельные директрисе, из фокуса F, проводят дуги (R1 и R2), равные расстоянию от директрисы до точек на оси параболы, точки пересечения дуг с прямыми будут принадлежать параболе.
Вариант Б
Из точки О (вершина параболы) перпендикулярно оси проводят прямую. Из точки В параллельно оси проводят прямую параллельно оси до пересечения с первой прямой в точке А. Отрезки ОА и АВ делят на одинаковое число равных частей. Вершину О соединяют с точками на прямой АВ. Из точек, лежащих на прямой ОБ проводят прямые параллельно оси параболы до пересечения с проведенными ранее прямыми. Полученные точки будут точками параболы.
Гипербола - это плоская кривая, разность расстояния от каждой точки которой до двух заданных точек F1 и F2 (фокусов) есть величина постоянная, равная расстоянию между вершинами гиперболы А1 и А2 .
|
|
| ||||||||||||||||
|
|
| |||||||||||||||||
Для построения гиперболы сначала проводят действительную ось х и мнимую ось У . В их пересечении лежит центр гиперболы (точка О), от которого строят влево и вправо фокусы F1 и F2 и вершины А1 и А2. Затем от одного из фокусов, например F2 , по действительной оси (в данном случае вправо) откладывают несколько отрезков произвольной длины. На рисунке отложено два таких отрезка, концы которых отмечены цифрами 1 и 2. Из фокусов F1 и F2 поочерёдно проводят дуги радиусом, равным расстоянию от построенных точек до вершин А1 и А2, из фокуса F2 радиусом R1 , равным расстоянию от точки 1 до вершины А2, из фокуса F1 проводят дугу радиусом R2, равным расстоянию от точки 1 до вершины А1. При пересечении дуг получают точки гиперболы. Построение выполняют слева и справа и от точки 2. Полученные точки соединяют.
Спираль Архимеда – плоская кривая которую описывает точка движущаяся равномерно поступательно от центра О по равномерно вращающемуся радиусу. Из центра О радиусом, равным t, выполнить окружность, которую разделить на 8 частей. Радиус t тоже разделить на 8 частей. Из центра О радиусом О1 провести дугу до пересечения с прямой, проведенной через точку 1 и центр О получим точку К1, принадлежащую спирали. Если провести дугу радиусом 02 до пересечения с прямой 02', получится очка К2 принадлежащая спирали, и т. д. При полном обороте отрезка О8 вокруг точки О отрезок совпадает со двоими начальным положением, а точка К займет положение К8 . Полученные точки Ко ... К8 соединяют плавной линией, которую обводят по лекалу.
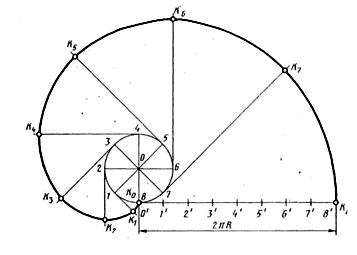
Эвольвента окружности - плоская кривая линия, представляющая собой траекторию точки окружности при её развёртывании.
Заданную окружность делят на любое число равных дуг (в данном случае на восемь), получают точки 1 .. 8. Каждую точку деления соединяют с центром окружности (точка О). Из точки 8 проводят касательную к окружности (2pR). Этот отрезок будет развернутой окружностью. Точка 8' будет принадлежать эвольвенте. Затем полученный отрезок делят на восемь равных частей и получают отрезки, равные 1/8 длины окружности, для определения длины каждой развёрнутой дуги. Далее через точки 1...8 проводят касательные и откладывают отрезки, равные длине соответствующей дуги. От точки 1 откладывают дуги О'1'. От точки 2 - отрезок, равный длине развёрнутой дуги О'2' и т. д. Получают точки K1 ... К8, принадлежащие эвольвенте. Полученные точки соединяют плавной кривой линией, которую обводят по лекалу.
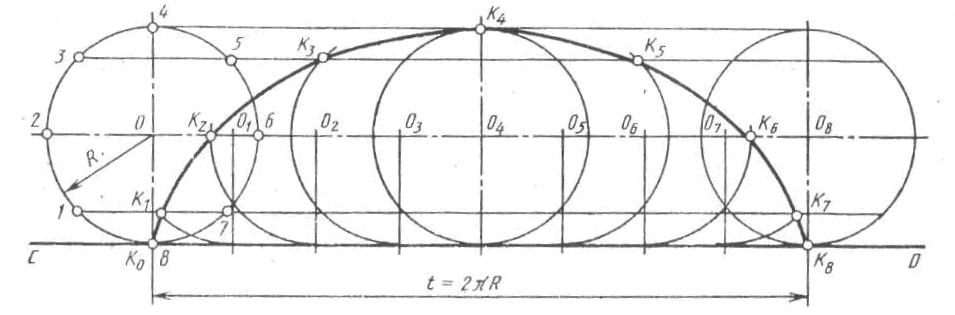
Циклоида – плоская кривая, описываемая точкой окружности, которая без скольжения катится по направляющей прямой. Точка К за один оборот окружности, катящейся прямой СД пройдет полный цикл кривой. Окружность за это время пройдет прямой путь, равный длине развернутой окружности, т. е. L = 2pR. Точка К после одного оборота окружности снова окажется на прямой CD в точке К8. Для определения промежуточных положений точки К через равные промежутки фиксируют положение этой точки. Для этого делят окружность на любое число равных частей, например, на восемь, получают точки 1....8, проводят из точки О линию центров, на которой отмечают восемь промежуточных положений центров (O1…O8) производящей окружности, разделив L =2pR на восемь равных частей. Когда окружность пройдёт 1/8 своего пути, точка К сместится вправо и вверх и окажется над направляющей прямой CD на такой же высоте, на которой находится точка 1.Поэтому для построения промежуточной точки К, из точки 1 проводят прямую, параллельную CD, а из центра О1 описывает часть окружности в её промежуточном положении радиусом R до пересечения с этой прямой. Это будет первое промежуточное положение точки К. Аналогично строят остальные точки. Соединив точки Ко…. К8 плавной тонкой линией от руки, получают циклоиду, которую обводят по лекалу.
Вопросы для закрепления материала:
1.Парабола - это плоская кривая, ___________________________________на одинаковое расстояние от заданной точки F (фокус) и заданной прямой АВ (директриса).
2.Эллипс – замкнутая плоская кривая____________________________________ до двух данных точек (фокусов) всегда равна длине большой оси эллипса.
3. Синусоида – плоская кривая, ______________________________________________ в зависимости от изменения его аргумента – угла α.
4. Гипербола - это плоская кривая, разность расстояния _________________________до двух заданных точек F1 и F2 (фокусов) _______________________________________, равная расстоянию между вершинами гиперболы А1 и А2 .
5. Спираль Архимеда – плоская кривая, движущаяся ________________________________О по равномерно вращающемуся радиусу.
6.Эвольвента окружности - плоская кривая линия, ________________________________
____________________________________________________________ при ее развертывании.
7.Циклоида – плоская кривая, которую описывает___________________________________
_______________________________________________________по направляющей прямой.
Построить спираль синусоиду Ø40мм.
Построить эвольвенту окружности Ø40мм
.
Построить циклоиду Ø40мм.
Построить параболу КF=20мм.
| F |
| К |
Построить спираль Архимеда R=50мм.
Построить гиперболу ОА1=ОА2=15мм, ОF1=OF2=30мм
Выполнить эллипс
Литература:
Основная литература:
1. Боголюбов С.К. Инженерная графика – М., «Машиностроение» 2015.
2. Бродский А.М., Фазлулин Э.М., Халдинов В.А. Практикум по инженерной графике – М., «Academia», 2015.
3. Исаев И.А. Инженерная графика – М., «Форум Инфра-М», 2015.
4. Каминский В.П., Иващенко Е.П. Инженерная и компьютерная графика графика – М., «Феникс» 2016.
5. Левицкий В.С. Машиностроительное черчение и автоматизация выполнения чертежей – М., «Юрайт», 2017.
6. Миронов Б.Г., Миронова Р.С, Пяткина А.А., Пузиков А.А. Сборник заданий по инженерной графике с примерами выполнения чертежей на компьютере – М., «Высшая школа», 2016.
Дополнительные источники:
1. Боголюбов С.К. Индивидуальные задания по курсу черчения – М., «Высшая школа», 1992.
2. Информатика. Техническая графика: учебное пособие для учащихся средних профессиональных учебных заведений. Истомина И.Г. – М., Издательский центр «Мир», 2005.
3. Лагерь А.И. Инженерная графика. М., «Высшая школа», 2004.
4. Фазлулин Э.М., Халдинов В.А. Инженерная графика - М., «Академия», 2006.
5. Чекмарев А.А. Справочник по машиностроительной графике – М., «Высшая школа», 1994.
6. Чекмарев А.А., Осипов В.Н. Справочник по машиностроительному черчению - М «Высшая школа» 2000г.
7. Чекмарев А.А. Инженерная графика. М., «Высшая школа», 2000.
Дата добавления: 2020-12-22; просмотров: 497; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!