Укажите в каких из этих положений величина приливов больше, а в каких меньше?
Найдите отношение сил гравитационного взаимодействия (сил тяготения) Луна-Земля и Солнце-Земля (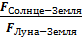 
).
Решение.
Новолуние. Силы тяготения со стороны Луны и Солнца действуют на поверхность Земли по одной прямой.
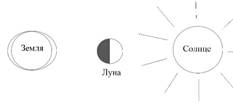
1 четверть. Силы тяготения со стороны Луны и Солнца действуют на поверхность Земли по одной прямой в перпендикулярных направлениях.
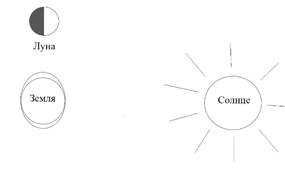
Полнолуние. Новолуние. Силы тяготения со стороны Луны и Солнца действуют на поверхность Земли по одной прямой.
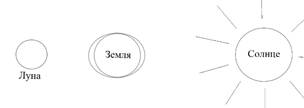
3 четверть. Силы тяготения со стороны Луны и Солнца действуют на поверхность Земли по одной прямой в перпендикулярных направлениях.
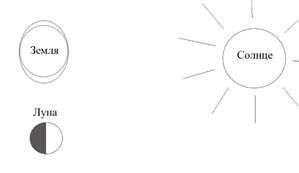
Величина приливов в положениях Луны «1 четверть» и «3 четверть» меньше, чем в положениях «Новолуние» и «Полнолуние». Это связано с тем, что в положениях Луны «1 четверть» и «3 четверть» гравитационные влияния Солнца и Луны действуют по одной прямой (сизигийные приливы), а в положениях «Новолуние» и «Полнолуние» - в перпендикулярных направлениях (квадратурные приливы).
Сила гравитационного взаимодействия двух тел с массами M и m, находящихся на расстоянии R друг от друга, определяется законом тяготения Ньютона:
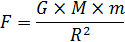
Таким образом, отношение сил взаимодействия Солнце-Земля и Луна-Земля равно
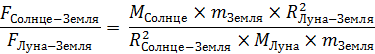
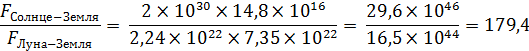
Критерии оценивания:
Правильная запись закона тяготения – 1 балл.
Верный расчет отношения сил гравитационного взаимодействия (сил тяготения) Луна-Земля и Солнце-Земля (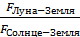 
) – 2 балла.
|
|
|
За каждое верное изображение приливов при различных фазах луны – по 1 баллу.
Правильный вывод о том, в каких положениях величина приливов больше – 1 балл.
3. Масса некой планеты в 6 раз больше массы Земли. Каков радиус этой планеты, если ускорение свободного падения на ее поверхности такое же, как на Земле?
Решение.
Как следует из второго закона Ньютона и закона всемирного тяготения,
,
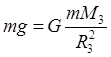m – масса тела, находящегося на поверхности Земли.
Отсюда
.
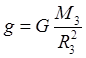Аналогично получаем
,
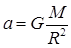здесь a – ускорение свободного падения на планете.
Приравняв выражения для a и g, находим
.
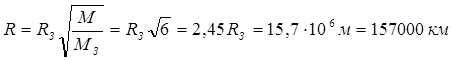Таким образом, радиус планеты равен 15700 км.
Оценивание:
Верный ответ без пояснения – 4 балла,
Развернутый ответ и верная формула расчета - 6 баллов,
Развернутый ответ, верная формула расчета и точные вычисления (без ошибки) – 8 баллов.
4. Как соотносятся синодические периоды внутренних и внешних планет и почему? (Необходимо дать определение синодического периода и привести формулы для расчета периодов и их отношения).
Решение.
Определение: синодическим периодом называется промежуток времени между одинаковыми фазами планеты при наблюдении ее с Земли.
|
|
|
Синодический период для внутренних планет может быть рассчитан по формуле:
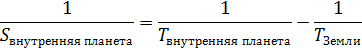
Где Т – сидерический (звездный) период планеты и Земли, поскольку Земля отстает в своем движении относительно внутренних планет (они движутся быстрее). Для Земли этот период равен 1 году. В земных годах эта формула может быть переписана следующим образом:
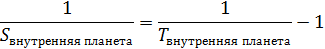
Для внешних планет ситуация – обратная: они движутся медленнее, чем Земля:
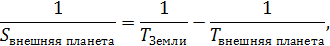
или
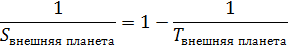
Следовательно, отношение синодических периодов внутренних и внешних планет может быть определено из уравнения:
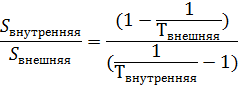
Оценивание:
Определение может быть дано в другой форме (например: синодический период планеты – это промежуток времени между ее двумя последовательными соединениями с Солнцем) и считается правильным, если в нем верно отражено содержание понятия – 2 балла.
Верная формула для определения синодического периода для внутренних планет – 2 балла.
Верная формула для определения синодического периода для внешних планет – 2 балла.
Верное выражение для отношения этих величин – 2 балла.
Дата добавления: 2020-12-22; просмотров: 151; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!