Цепь с идеальным индуктивным элементом.
Примером идеального индуктивного элемента может служить индуктивная катушка. Электрическая энергия, выделяемая в катушке за счет нагрева провода обмотки, как правило, невелика, как и межвитковая емкость, и во многих практических случаях ими можно пренебречь (R=0, C=0). При принятых допущениях индуктивную катушку называют идеальным индуктивным элементом цепи или L-элементом.
Параметром идеального индуктивного элемента является индуктивность L, а энергетические процессы в нем определяются только явлениями, происходящими в магнитном поле.
Индуктивность — коэффициент пропорциональности между электрическим током, текущим в каком-либо замкнутом контуре, и магнитным потоком, создаваемым этим током через поверхность, краем которой является этот контур. На электрических схемах используют условные графические обозначения катушек индуктивностей, примеры которых приведены на рисунке 4.
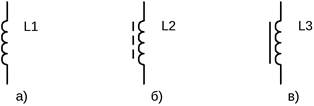
Рисунок 4- Условные графические обозначения индуктивностей:
а – обозначение катушки индуктивности; б – с магнитодиэлектрическим сердечником;
в – с ферромагнитным сердечником
При прохождении электрического тока по катушке, ток создаст переменный магнитный поток Ф.Силовые линии этого потока, пересекая витки катушки, будут индуктировать в ней э.д.с. самоиндукции. По закону электромагнитной индукции
eL=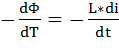 
Так как в цепи, куда включена индуктивность L, отсутствует активное сопротивление (рассматривается идеальная катушка индуктивности), то по второму закону Кирхгофа u+eL=0, т. е. u = -eL. Следовательно, напряжение источника всегда равно по величине и противоположно по направлению э. д. с. самоиндукции.
|
|
|
Если в формулу подставить значение тока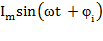 
и продифференцировать, то получим:
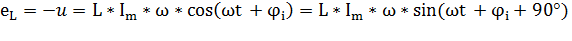
Обозначим величину ωL·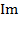 
равной амплитуде напряжения Um. Тогда по закону Ома
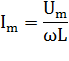
Величину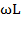 
называют индуктивным сопротивлением, измеряют в Омах и обозначают
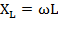
Так как 
, то начальную фазу напряжения можно представить как φu= φi+ 90и, следовательно,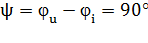 
Выведенное соотношение показывает, что если в катушке протекает синусоидальный ток, то напряжение также имеет синусоидальный характер, но при этом оно опережает ток на четверть периода (90°) (рисунок 5).
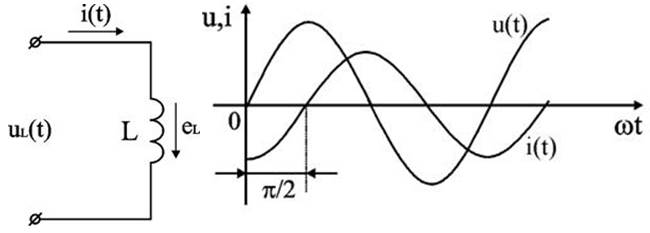
Рисунок 5-Цепь с индуктивным сопротивлением и её векторная диаграмма
Цепь с идеальным емкостным элементом .
Конденсатор – элемент электрической цепи, предназначенный для использования его ёмкости. В конденсаторе накапливается энергия электрического поля. Свойство элемента запасать электрический заряд характеризует ёмкость (С). Этот параметр является коэффициентом пропорциональности между зарядом q (Кл) и прикладываемым напряжением u (В).
|
|
|
q = C·u,
При изменении напряжения на конденсаторе изменяется заряд и возникает электрический ток
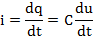
Идеализированный конденсатор обладает только ёмкостью С (R=0, L=0).
Рассмотрим электрические процессы в цепи с идеальным ёмкостным элементом. Пусть напряжение источника изменяется по закону u = Um·sinωt, (φu = 0).
В цепи возникает ток
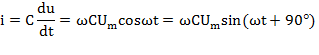
Из полученного выражения видно, что начальная фаза тока φi =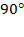 
. Угол сдвига фаз между напряжением и током составляет
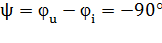
Следовательно, синусоида напряжения на емкости отстаёт от синусоиды тока на угол 90°. На практике, если в электрической цепи напряжение отстаёт по фазе от тока, говорят об ёмкостном характере нагрузки (рисунок 6).
Амплитуда тока будет равна Im = ω·C·Um=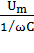 
.
Величину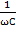 
называют ёмкостным сопротивлением конденсатора и измеряют в Омах
Xc=1/ ω•C =1/2πfC.
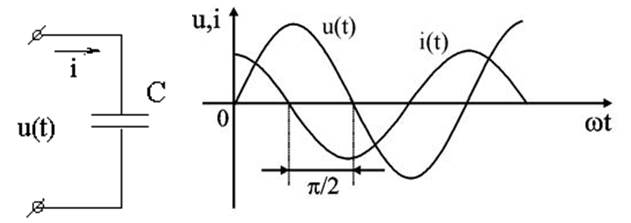
Рисунок 6- Цепь с емкостным сопротивлением и её векторная диаграмма
Итак, в цепях переменного тока выделяют следующие виды сопротивлений:
- активное (активным называют сопротивление резистора). Единицей измерения сопротивления является Ом. Сопротивление резистора не зависит от частоты сети.
- реактивное (индуктивное XL и емкостное ХС). Единицей измерения индуктивного и емкостного сопротивления также является Ом. Величина индуктивного сопротивления линейно зависит от частоты. А величина ёмкостного сопротивления обратнопропорциональна частоте сети. В цепях со смешанным соединением нагрузки (активной, индуктивной, ёмкостной) реактивным сопротивлением цепи называют величину
|
|
|
X = XL - XC.
Для того, чтобы найти общее сопротивление электрической цепи со смешанным соединением нагрузки используют понятие полного сопротивления цепи, которое определяется как
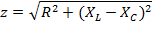
Дата добавления: 2020-12-22; просмотров: 140; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!