Примеры для самостоятельного решения
СЕМИНАР 12
Определённый интеграл
Пусть на отрезке [a ; b] задана непрерывная неотрицательная функция y = f(x) (рисунок).
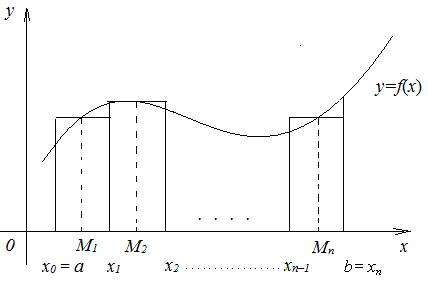
Определение 1. Сумма 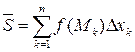 называется интегральной суммой функции f (x) на отрезке [a ; b].
называется интегральной суммой функции f (x) на отрезке [a ; b].
Определение 2. Предел интегральных сумм 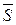 функции f (x) на отрезке [a ; b] при n ® ¥ и max D xk ® 0 называется определённым интегралом функции f(x) на отрезке [a ; b], если этот предел существует и не зависит ни от способа разбиения отрезка [a ; b] на части, ни от выбора точек Mk (k = 1,…, n) на каждой из частей. Следовательно, можно записать:
функции f (x) на отрезке [a ; b] при n ® ¥ и max D xk ® 0 называется определённым интегралом функции f(x) на отрезке [a ; b], если этот предел существует и не зависит ни от способа разбиения отрезка [a ; b] на части, ни от выбора точек Mk (k = 1,…, n) на каждой из частей. Следовательно, можно записать:
 .
.
При этом отрезок [a ; b] называют отрезком интегрирования, «a»–нижним пределом интегрирования,«b»–верхним пределом.
Достаточное условие интегрируемости функции на отрезке [a ; b].Если функция f(x) на отрезке [a ; b] непрерывна, то определённый интеграл 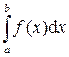 существует, т.е. функция f (x) на отрезке [a ; b] интегрируема.
существует, т.е. функция f (x) на отрезке [a ; b] интегрируема.
Свойства определённого интеграла
1) 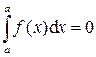
2) 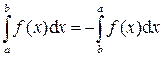
3) 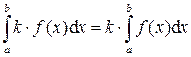
4) 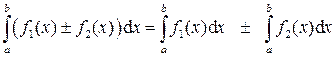
5) Если функция f(x) интегрируема на отрезках [a ; c] и [c ; b], то она интегрируема и на отрезке [a ; b], причём верно равенство:
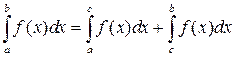
при любом расположении точек a , b и c на оси Ox.
6) Если f (x) ³ 0 при x Î [a ; b], то
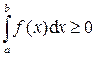
7) Если на отрезке [a ; b] f (x) ³ g (x), то

8) Теорема 1 (о среднем значении определённого интеграла).Если функция f (x) непрерывна на отрезке [a ; b], то на этом отрезке найдётся хотя бы одна точка c, в которой выполняется равенство:
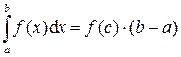
Формула Ньютона–Лейбница
Теорема 2. Пусть функция f (x) непрерывна на отрезке [a ; b] и F(x) – какая-либо её первообразная на отрезке [a ; b]. Тогда определённый интеграл от функции f(x) по отрезку [a ; b] равен разности значений функции F(x) в точках b и a:
|
|
|

Формула Ньютона–Лейбница является основной формулой интегрального исчисления, устанавливающей связь между определённым и неопределённым интегралами, и даёт правило вычисления определённого интеграла.
Замечание. Формулу Ньютона–Лейбница часто записывают в виде:
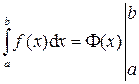 ,
,
где используется обозначение:
 .
.
Задача вычисления определённого интеграла сводится к нахождению первообразной непрерывной функции.
Методы интегрирования определённого интеграла
Замена переменной в определённом интеграле
Теорема 3. Пусть функция f(x) непрерывна на отрезке [a ; b] и пусть функция x = j(t) имеет непрерывную производную j'(t) на отрезке [a;b], область значений этой функции – отрезок [a ; b], т.е. a £ j (t) £ b для tÎ [a;b], причём j(a) = a, j(b) = b.
Тогда справедливо равенство:
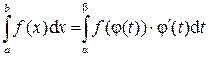 .
.
2) Интегрирование по частям в определённом интеграле
Теорема 4. Пусть функции u(x) и v(x) имеют непрерывные производные на отрезке [a;b]. Тогда справедливо равенство:
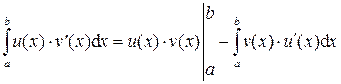 .
.
Примеры с решениями
Пример 1. Вычислить интеграл 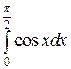
|
|
|
Решение.


Ответ: 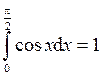 .
.
Пример 2. Вычислить интеграл 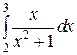
Решение.
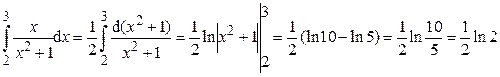 .
.
Ответ: 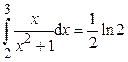 .
.
Пример 3. Вычислить интеграл 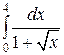
Решение.
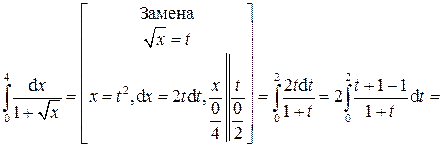
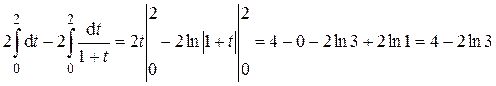 .
.
Ответ: 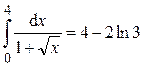 .
.
Пример 4. Вычислить интеграл 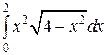
Решение.
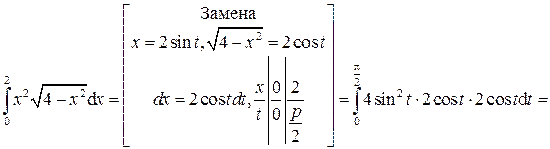
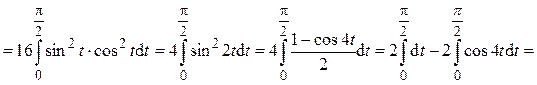
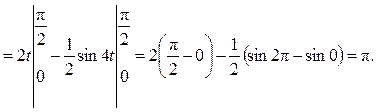
Ответ: 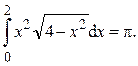
Пример 5. Вычислить интеграл 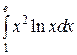
Решение.
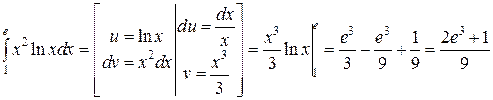
Ответ: 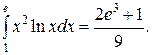
Пример 6. Вычислить интеграл 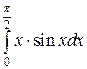
Решение.
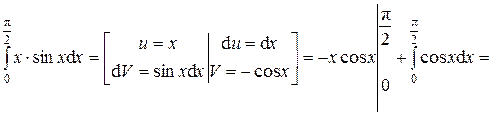
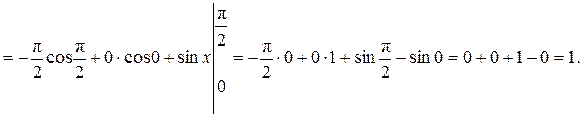
Ответ: 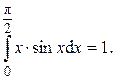
Примеры для самостоятельного решения
1.  4.
4. 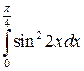
2.  5.
5. 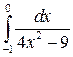
3. 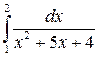 6.
6. 
7. 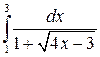 20.
20. 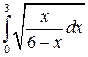
8. 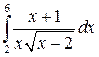 21.
21. 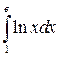
9. 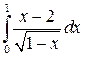 22.
22. 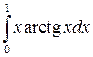
10. 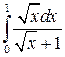 23.
23. 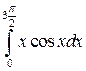
11. 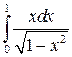 24.
24. 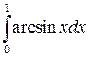
12. 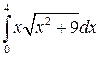 25.
25. 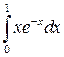
13. 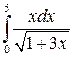 26.
26. 
14. 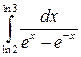 27.
27. 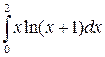
15. 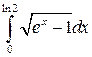 28.
28. 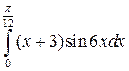
16. 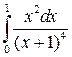 29.
29. 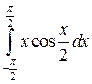
17. 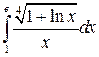 30.
30. 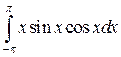
18. 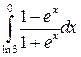 31.
31. 
|
|
|
19. 
Ответы

Дата добавления: 2020-12-22; просмотров: 47; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
