Дифференциальные уравнения первого порядка.
ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ
Государственное образовательное учреждение высшего профессионального
образования
«Ковровская государственная технологическая академия имени
В.А. Дегтярева»
Интегралы. Дифференциальные уравнения.
Контрольная работа по математике для заочного отделения.
Миронова Е.А.
Юлина Н.А.
г. Ковров 2013 г.
Методические указания предназначены в качестве пособия для студентов заочного отделения технических специальностей. Содержат в себе сжатый теоретический материал и индивидуальные задания к контрольной работе по математике, а так же решение типового варианта.
Введение
Настоящее учебно-методическое пособие содержит краткие теоретические сведения из разделов «Интегрирование функции одного аргумента» и «Обыкновенные дифференциальные уравнения», включая технические приложения. Пособие содержит условия контрольной работы по этим темам, которая состоит из 15 заданий и представлена 30 вариантами, а также пример выполнения типового варианта. Задания для контрольной работы студентов включают основные задачи из интегрального исчисления и теории решения дифференциальных уравнений. В конце пособия приведён список использованной и рекомендуемой для самостоятельной подготовки литературы.
|
|
|
Содержание пособия подчинено требованиям современного государственного образовательного стандарта по математике для студентов технических специальностей. Краткие теоретические сведения, изложенные в пособии, даны в объёме, достаточном для самостоятельного решения заданий.
Задания для контрольной работы подобраны исходя из опыта работы преподавателей кафедры «Высшая математика» КГТА и с учётом уровня подготовки студентов заочного отделения, что выгодно отличает данное пособие от ранее изданных аналогичных пособий.
Пособие может быть использовано для самостоятельного изучения указанных разделов студентами не только заочного отделения. Задания для контрольной работы могут быть использованы преподавателями в своей работе для организации аудиторной самостоятельной работы студентов других форм обучения.
Интегральное исчисление функции одного действительного аргумента.
Неопределённый интеграл.
Функция  называется первообразной функции
называется первообразной функции 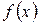 , если
, если 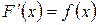 на
на  и
и 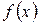 определена и непрерывна на
определена и непрерывна на  . Если
. Если  – первообразная для функции
– первообразная для функции 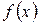 , то множество функций
, то множество функций 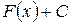 называется неопределённым интегралом от функции
называется неопределённым интегралом от функции 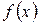 и обозначается символом
и обозначается символом
|
|
|
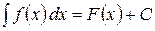 ,
,
где 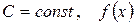 – подынтегральная функция,
– подынтегральная функция, 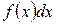 – подынтегральное выражение, а
– подынтегральное выражение, а 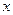 – переменная интегрирования.
– переменная интегрирования.
Восстановление функции по её производной называется интегрированием.
Основные свойства неопределённого интеграла.
1.  .
.
2. 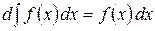 .
.
3. 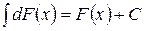 .
.
4.  ,
, 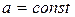 .
.
5. 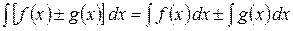 .
.
6. Если 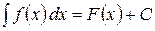 и
и 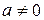 , то
, то 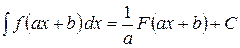 .
.
7. Если  , то
, то 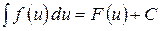 .
.
Основные интегралы от элементарных функций:
1. 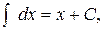
2. 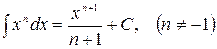 ,
,
3. 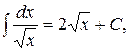
4.  ,
,
5. 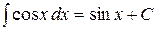 ,
,
6. 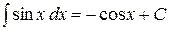 ,
,
7. 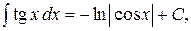
8. 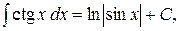
9. 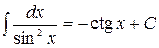 ,
,
10. 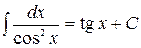 ,
,
11. 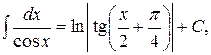
12. 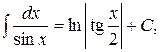
13. 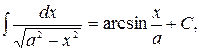
14. 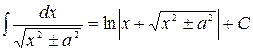 ,
,
15. 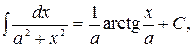
16. 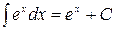 ,
,
17. 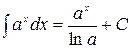 ,
,
18. 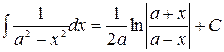 ,
,
19. 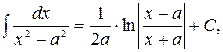
20. 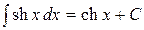 ,
,
21. 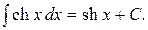
Рассмотрим основные методы интегрирования.
Непосредственное интегрирование – это метод интегрирования, при котором данный интеграл путем тождественных преобразований подынтегральной функции и применение свойств неопределенного интеграла приводится к табличному интегралу.
Замена переменной. Если 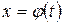 – непрерывно дифференцируемая функция и
– непрерывно дифференцируемая функция и 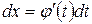 , то
, то
 . (1.1)
. (1.1)
Внесение под знак дифференциала. Метод внесения под знак дифференциала является частным случаем метода замены переменных.
Метод основан на 7 свойстве формул интегрирования. Формула интегрирования сохраняет свой вид при подстановке вместо переменной любой дифференцируемой функции от этой переменной.
При приведении данного интеграла 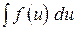 к табличному виду используют следующие преобразования дифференциала:
к табличному виду используют следующие преобразования дифференциала:
|
|
|
1.  , где
, где  ,
,
2. 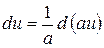
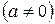 ,
,
3. 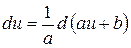 ,
,
где  и
и  – const,
– const,
4. 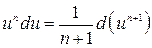
5.  ,
,
6.  ,
,
7. 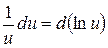 ,
,
8.  ,
,
9. 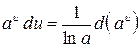 ,
,
10. 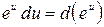 ,
,
11. 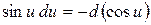 ,
,
12. 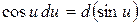 ,
,
13. 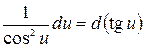 ,
,
14. 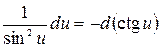 ,
,
15. 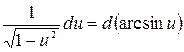 ,
,
16.  .
.
В общем виде формула метода внесения под знак дифференциала выглядит так:
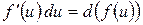 .
.
Интегрирование по частям. Пусть  и
и 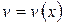 непрерывно дифференцируемые функции, тогда
непрерывно дифференцируемые функции, тогда
 . (1.2)
. (1.2)
Для нахождения неопределённого интеграла можно воспользоваться системой MathCad. Для этого необходимо ввести оператор неопределённого интеграла с панели Calculus (вычисления) и в соответствующем местозаменителе напечатать имя переменной, по которой должно быть осуществлено интегрирование, а также ввести функцию, для которой требуется найти неопределённый интеграл. Следует обратить внимание на то, что MathCad выводит только основное значение первообразной функции, без постоянной величины.
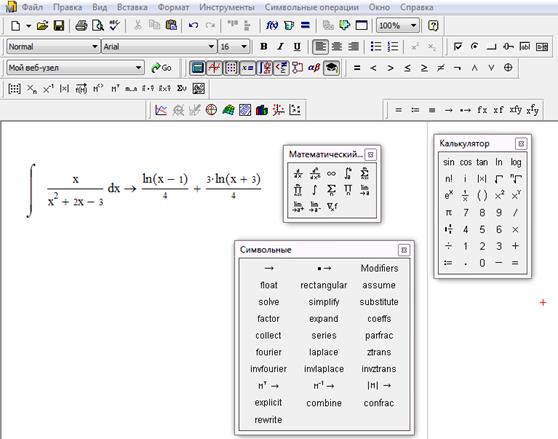
Рис. 1 Пример вычисления неопределённого интеграла в системе MathCad
Определённый интеграл.
Пусть функция  определена на отрезке
определена на отрезке 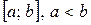 . Разобьём этот отрезок на n произвольных частей точками
. Разобьём этот отрезок на n произвольных частей точками 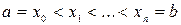 .
.
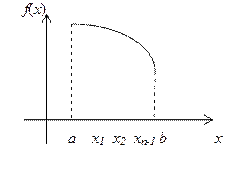
Рис. 17
В каждом из полученных частичных отрезков 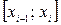 выберем произвольную точку
выберем произвольную точку 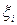
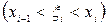 и составим сумму:
и составим сумму:
|
|
|
 ,
,
где  . Эта сумма называется интегральной суммой для функции
. Эта сумма называется интегральной суммой для функции  на
на 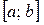 . Обозначим
. Обозначим 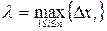 (т.е. длина наибольшего частичного отрезка).
(т.е. длина наибольшего частичного отрезка).
Если существует конечный предел I интегральной суммы s при 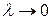 (
( 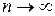 ), то этот предел называется определённым интегралом от функции
), то этот предел называется определённым интегралом от функции 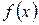 по
по 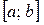 и обозначается
и обозначается
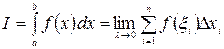 .
.
В этом случае 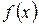 называется интегрируемой на
называется интегрируемой на 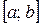 . Числа a и b называются соответственно нижним и верхним пределом интегрирования.
. Числа a и b называются соответственно нижним и верхним пределом интегрирования.
Основные свойства определённого интеграла.
1. 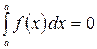 .
.
2. 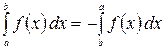 .
.
3.  .
.
4. 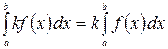 ,
, 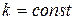 .
.
5.  .
.
6.  , где
, где 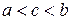 .
.
7. Если  при
при 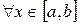 , то
, то 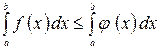 .
.
8. Если  при
при 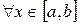 , то
, то 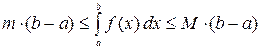 .
.
9. Если функция 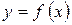 непрерывна на отрезке
непрерывна на отрезке 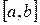 , то найдется такая точка
, то найдется такая точка  , такая, что
, такая, что 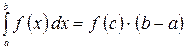 . Число
. Число 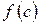 называется средним значением функции
называется средним значением функции 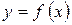 на отрезке
на отрезке 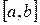 .
.
10. 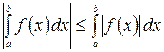 , при
, при 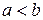 .
.
11. 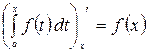 .
.
Основные методы интегрирования.
Формула Ньютона-Лейбница. Если функция 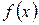 определена и непрерывна на отрезке
определена и непрерывна на отрезке 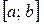 , а
, а 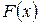 – какая-либо её первообразная, т.е.
– какая-либо её первообразная, т.е. 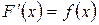 , то
, то
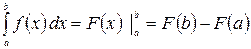 . (1.3)
. (1.3)
Формула интегрирования по частям. Если 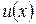 и
и 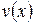 – непрерывно интегрируемы на
– непрерывно интегрируемы на 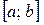 функции, то
функции, то
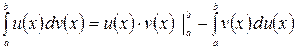 . (1.4)
. (1.4)
Замена переменной. Если функция 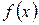 непрерывна на отрезке
непрерывна на отрезке 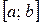 ,
, 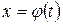 – непрерывно дифференцируемая функция на
– непрерывно дифференцируемая функция на 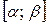 , где
, где 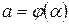 ,
, 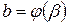 и
и 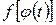 определена и непрерывна на
определена и непрерывна на 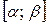 , то
, то
 . (1.5)
. (1.5)
Определённый интеграл применяют для вычисления площади криволинейной трапеции. Если криволинейная трапеция ограничена сверху графиком функции  , слева и справа – прямыми
, слева и справа – прямыми 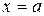 и
и 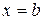 , снизу – осью Ох, то площадь вычисляется по формуле
, снизу – осью Ох, то площадь вычисляется по формуле
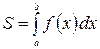 . (1.6)
. (1.6)
Площадь криволинейной фигуры, ограниченной сверху графиком функции  , снизу – графиком функции
, снизу – графиком функции 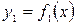 , слева и справа – прямыми
, слева и справа – прямыми  и
и 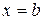 , вычисляется по формуле
, вычисляется по формуле
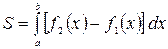 . (1.7)
. (1.7)
Определенный интеграл с бесконечным пределом интегрирования называется несобственным интегралом. Пусть функция 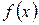 непрерывна на интервале
непрерывна на интервале 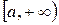 , тогда несобственный интеграл имеет вид:
, тогда несобственный интеграл имеет вид:
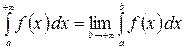 . (1.8)
. (1.8)
К несобственным относятся так же и интегралы
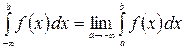 и
и 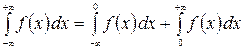 .
.
Систему MathCad можно использовать и для нахождения определённого интеграла. Для этого нужно ввести символ определённого интеграла с панели Calculus (вычисления) с несколькими местозаменителями, в которые нужно ввести нижний и верхний пределы интегрирования, подынтегральную функцию и переменную интегрирования. Чтобы получить результат интегрирования, следует ввести знак равенства для получения ответа в виде десятичной дроби (Рис.2 а) или символьного равенства для получения точного ответа (Рис.2 б).
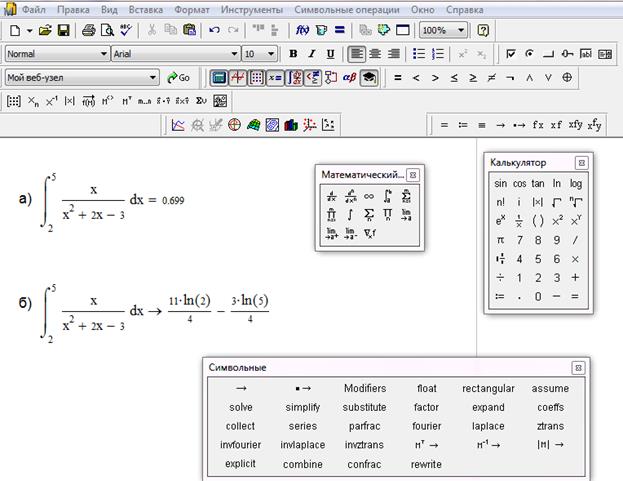
Рис. 2 Пример вычисления определённого интеграла в системе MathCad
Дифференциальные уравнения.
Дифференциальные уравнения первого порядка.
Уравнение вида 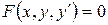 , где
, где  – независимая переменная,
– независимая переменная, 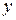 – искомая функция,
– искомая функция, 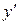 – её производная, называется дифференциальным уравнением первого порядка.
– её производная, называется дифференциальным уравнением первого порядка.
Решением дифференциального уравнения первого порядка называется функция, которая при подстановке в уравнение превращает его в тождество.
Условие, что при 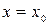 функция
функция 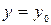
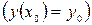 называется начальным условием.
называется начальным условием.
Функция, 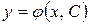 , содержащая одну произвольную постоянную называется общим решением. Функция
, содержащая одну произвольную постоянную называется общим решением. Функция 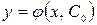 , полученная из общего решения и удовлетворяющая начальному условию, называется частным решением.
, полученная из общего решения и удовлетворяющая начальному условию, называется частным решением.
Рассмотрим методы интегрирования некоторых уравнений первого порядка.
Уравнение с разделяющимися переменными – это уравнение вида:
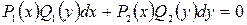 , (2.1)
, (2.1)
где 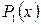 ,
, 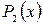 ,
, 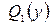 и
и  – известные функции, зависящие только от
– известные функции, зависящие только от 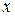 или
или 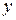 .
.
Если ни одна из этих функций не равна тождественно нулю, то разделив уравнение (2.1) на 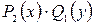 , получим уравнение с разделенными переменными:
, получим уравнение с разделенными переменными:
 . (2.2)
. (2.2)
Проинтегрировав это уравнение, получим общее решение исходного уравнения:
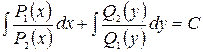 . (2.3)
. (2.3)
Уравнение  сводится к уравнению с разделенными переменными. Учитывая, что
сводится к уравнению с разделенными переменными. Учитывая, что 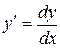 , получим уравнение вида:
, получим уравнение вида:
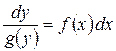 . (2.4)
. (2.4)
Линейное уравнение – это уравнение вида:
 , (2.5)
, (2.5)
где 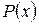 и
и  – заданные функции.
– заданные функции.
Для решения его рассмотрим метод Бернулли. Выполним подстановку 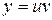 , где
, где 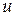 и
и 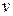 – две неизвестные функции, причем одна из которых произвольная. Тогда уравнение (2.5) сводится у виду
– две неизвестные функции, причем одна из которых произвольная. Тогда уравнение (2.5) сводится у виду
 или
или 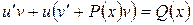 . (2.6)
. (2.6)
Предполагая, что  – произвольная функция, найдем одно из ее решений из уравнения
– произвольная функция, найдем одно из ее решений из уравнения 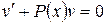 , например,
, например,
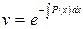 . (2.7)
. (2.7)
Тогда уравнение (2.6) сведется к виду:
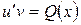 или
или  , т.е.
, т.е. 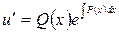 . (2.8)
. (2.8)
Решая уравнение (2.8), получим:
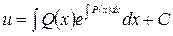 . (2.9)
. (2.9)
Общее решение исходного уравнения находится умножением 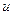 на
на 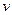 :
:
 . (2.10)
. (2.10)
Дата добавления: 2020-12-22; просмотров: 67; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
