П. 27. Комплексные числа и действия над ними.
Приходовский М.А.
Алгебра
(электронное учебное пособие по практике)
ИПМКН ТГУ, группы 932024, 932025
Осень - 2020
ПРАКТИКА 1.
Задача 1. Образует ли группоид следующее множество с данной бинарной операцией 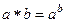 ? а)
? а) 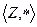 , б)
, б) 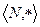 .
.
а) Не образует, так как, например, 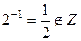 .
.
б) Образует, положительная степень положительного числа это снова натуральное число.
Задача 2. Образует ли группоид следующее множество с данной операцией? 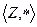 ,
, 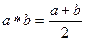 .
.
Не образует, так как, например, 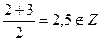 .
.
Задача 3. Какое из множеств: 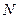 ,
,  ,
, 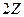 является группоидом с операцией
является группоидом с операцией 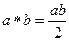 ?
?
а) рассмотрим 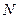 . Не для всяких двух натуральных чисел результат операции снова лежит в этом множестве.
. Не для всяких двух натуральных чисел результат операции снова лежит в этом множестве. 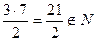 .
.
б) рассмотрим  . Если даны 2 рациональных числа, то
. Если даны 2 рациональных числа, то 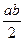 рациональное число, т. е.
рациональное число, т. е. 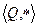 - группоид.
- группоид.
в) рассмотрим  - множество всех чётных чисел. Тогда
- множество всех чётных чисел. Тогда 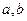 можно записать в виде
можно записать в виде 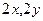 , 0,5(2х*2у) = 2ху снова чётное число.
, 0,5(2х*2у) = 2ху снова чётное число.
Значит, 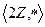 - группоид.
- группоид.
Задача 4. Является ли группоид коммутативным:
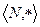 , где
, где 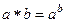 .
.
Нет, контрпримеров много, 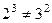 ,
, 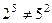 и т.д.
и т.д.
Задача 5. Является ли группоид коммутативным:
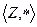 , где
, где 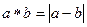 .
.
Так как  , является.
, является.
Является ли группоид полугруппой (т.е. есть ли ассоциативность?)
* Задача 6. 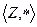 , где
, где 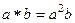 .
.
Проверяем.
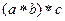 =
= 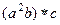 =
=  =
=  .
.
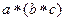 =
= 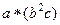 =
= 
Не совпадают. Ассоциативности нет. Комм тоже нет.
Задача 7. 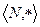 , где
, где 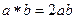 .
.
Проверяем для произвольных элементов.
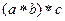 =
= 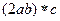 =
= 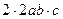 =
= 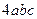 .
.
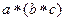 =
= 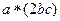 =
= 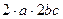 =
= 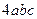 .
.
Результаты совпадают. Ассоциативность есть.
* Задача 8. 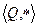 ,
, 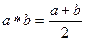 .
.
|
|
|
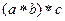 =
= 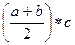 =
= 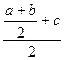 =
= 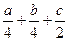 .
.
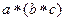 =
= 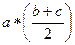 =
= 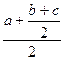 =
=  .
.
Не совпадают. Ассоциативности нет.
Задача 9. 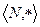 , где
, где 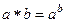 .
.
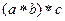 =
= 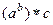 =
= 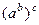 =
= 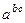 .
.
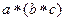 =
= 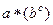 =
= 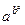 .
.
Но ведь  , так что
, так что 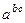

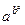 .
.
Не совпадают. Ассоциативности нет.
Задача 10. 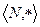 , где
, где  (операция оставляет только первый элемент).
(операция оставляет только первый элемент).
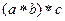 =
= 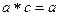
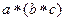 =
= 
Результаты совпадают. Ассоциативность есть.
Задача 11.
Указать нейтральный элемент (если он существует) в группоидах.
11.1. 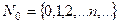 относительно операции
относительно операции 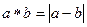 . Ответ. 0.
. Ответ. 0.
11.2. 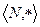 , где
, где 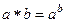 . Правый нейтральный элемент 1.
. Правый нейтральный элемент 1.
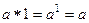
Левый не существует. Допустим, 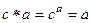 , тогда
, тогда
 , т.е. логарифм по некоторому основанию был бы тождественной функцией.
, т.е. логарифм по некоторому основанию был бы тождественной функцией.
11.3. 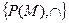 - множество всех подмножеств относительно операции пересечения.
- множество всех подмножеств относительно операции пересечения.  , само множество.
, само множество.
11.4. 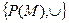 - множество всех подмножеств относительно операции объединения.
- множество всех подмножеств относительно операции объединения. 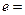
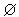 - пустое множество .
- пустое множество .
11.5 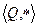 , где
, где 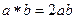 .
.
2ае = а 2е = 1 реш. ****
 ,
, 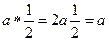 .
.
* Задача 12. Проверить ассоциативность и наличие нейтрального элемента для  , где
, где 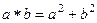 .
.
Решение. 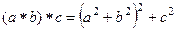 =
=  .
.
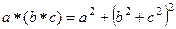 =
= 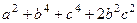 .
.
Ассоциативность отсутствует.
Если 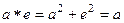 ,
, 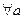 , то
, то  , но очевидно, что
, но очевидно, что  принимает разные значения при разных
принимает разные значения при разных 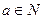 , и не может быть равно одному и тому же
, и не может быть равно одному и тому же  . Нейтральный элемент не существует.
. Нейтральный элемент не существует.
- - - перерыв - - -
* Задача 13. Пусть 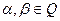 . Является ли отображение
. Является ли отображение 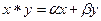 ассоциативной операцией в
ассоциативной операцией в  ?
?
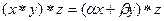 =
= 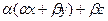 =
=  .
.
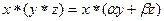 =
=  =
= 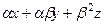 .
.
Ассоциативности нет.
|
|
|
Задача 14. Исследовать операцию вычисления наибольшего общего делителя (НОД). 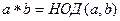 .
.
(коммутативность, ассоциативность, дистрибутивность относительно сложения, нейтральный элемент).
Решение. Коммутативность: Если 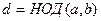 , то
, то 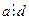 и
и  , это равносильно
, это равносильно  и
и 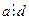 . Т.е.
. Т.е. 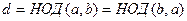 .
.
Ассоциативность  .
.
Наибольшее натуральное число, являющееся делителем всех трёх исходных чисел.
Дистрибутивность. 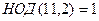 , это взаимно простые числа. В то же время,
, это взаимно простые числа. В то же время, 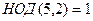 ,
, 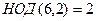 .
.
Таким образом, есть контрпример, показывающий, что
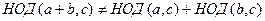 .
.
Нейтрального элемента не существует. Допустим, что какое-то натуральное число 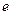 обладает свойством:
обладает свойством: 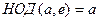 .
.
Тогда 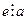 . Но если это
. Но если это 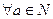 , значит,
, значит, 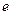 должно делиться на все натуральные числа, то есть оно больше любого натурального числа.
должно делиться на все натуральные числа, то есть оно больше любого натурального числа.
Задача 15. Доказать, что если 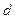 НОД чисел
НОД чисел 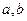 , то существуют такие
, то существуют такие 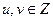 , что
, что  .
.
Решение. Рассмотрим множество чисел 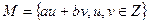 .
.
Докажем, что если 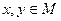 , то остаток от деления одного на второе из них тоже
, то остаток от деления одного на второе из них тоже 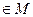 .
.
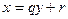 . Но ведь
. Но ведь 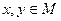 и их можно представить так:
и их можно представить так:
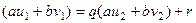 . Тогда
. Тогда
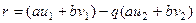 =
=  , где
, где
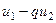 ,
, 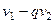 целые числа. То есть,
целые числа. То есть, 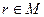 .
.
Теперь рассмотрим наименьшее положительное число 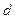 из множества
из множества 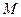 . Оно и является НОД (
. Оно и является НОД ( 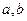 ), по следующей причине. Остаток от деления
), по следующей причине. Остаток от деления 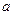 (или
(или 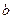 ) на
) на 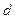 должен
должен 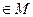 , как доказано ранее. Но тогда было бы положительное число, меньшее чем
, как доказано ранее. Но тогда было бы положительное число, меньшее чем 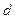 , в этом множестве. А это невозможно, т.к.
, в этом множестве. А это невозможно, т.к. 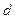 наименьшее. Поэтому
наименьшее. Поэтому 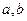 делятся на
делятся на 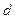 без остатка.
без остатка.
|
|
|
Теперь о том, почему 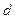 наибольший общий делитель. Если
наибольший общий делитель. Если 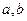 делятся на какое-то другое число
делятся на какое-то другое число 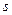 , то
, то  тоже делится на
тоже делится на 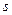 , так как оба слагаемых делятся на
, так как оба слагаемых делятся на 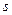 .
.
Следствие. Если 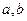 взаимно просты, то существуют такие
взаимно просты, то существуют такие 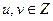 , что
, что  .
.
Примеры к задаче 15. Найдутся такие 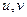 , и причём даже не единственным образом, что
, и причём даже не единственным образом, что 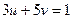 , 3 и 5 взаимно просты.
, 3 и 5 взаимно просты.

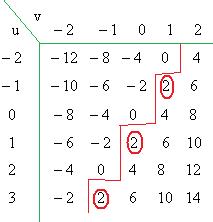
Среди множества натуральных чисел вида 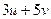 , наименьшее именно 1, так как числа 3 и 5 взаимно просты.
, наименьшее именно 1, так как числа 3 и 5 взаимно просты.
(Таблица бесконечная во все стороны, показан фрагмент).
Составим такую же таблицу для чисел 2 и 4. НОД (2,4) = 2.
Операция умножения матриц.
Рассмотрим квадратные матрицы порядка 2.
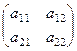
Каждый элемент обозначается 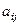 , где
, где  это номер строки, в которой он расположен, а
это номер строки, в которой он расположен, а 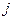 - номер столбца.
- номер столбца.
Сложение матриц.
Эта операция определяется поэлементно, то есть суммируется каждая соответствующая пара элементов 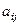 и
и  .
.
Пример: 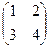 +
+ 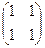 =
= 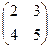 .
.
* Сложение коммутативно и ассоциативно. Нейтральный элемент по сложению - нулевая матрица 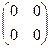 .
.
Умножение матрицы на константу. В матрице 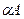 все элементы умножены на коэффициент
все элементы умножены на коэффициент 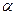 , то есть равны
, то есть равны 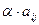 .
.
Так как константа может быть и 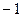 , то определено в том числе и вычитание матриц.
, то определено в том числе и вычитание матриц.
|
|
|
Тот же пример, но разность (устно).
Умножение двух матриц.
* Надо вспомнить из школьного курса операцию скалярного произведения двух векторов: 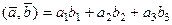
Операция умножения матриц определяется следующим образом. Мысленно разобьём первую матрицу на строки, вторую - на столбцы. Для каждой строки 1-й матрицы и каждого столбца 2-й матрицы определено скалярное произведение. Именно из них и состоит произведение.
2 примера: 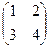
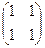 =
= 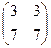 ,
, 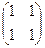
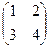 =
= 
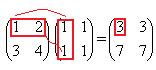
обратите внимание, что даже для квадратных матриц далеко не всегда выполняется закон коммутативности, здесь 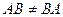 .
.
Ещё примеры:
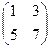
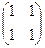 =
= 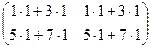 =
= 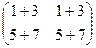 =
=  .
.
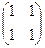
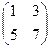 =
= 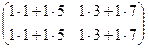 =
= 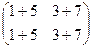 =
=  .
.
Докажем отсутствие коммутативности в общем случае:
 =
= 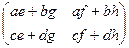
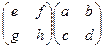 =
= 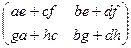
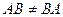
Проверка ассоциативности.
 =
= 
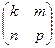 =
=
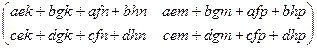 .
.
С другой стороны, 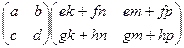 =
=
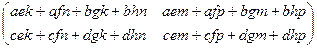 .
.
Нейтральный элемент Е.
Существует такая матрица, которая во множестве матриц обладает свойством, аналогичным 1 во множестве чисел, то есть  . Но как мы видели только что, матрица из всех единиц этим свойством не обладает, а вот если единицы только по главной диагонали, а вокруг - нули, то такое свойство будет выполняться.
. Но как мы видели только что, матрица из всех единиц этим свойством не обладает, а вот если единицы только по главной диагонали, а вокруг - нули, то такое свойство будет выполняться.
Единичная матрица Е. Строение: 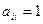 ,
, 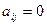 при
при 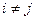 .
.
Е = 
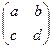
 =
=  =
= 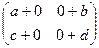 =
= 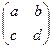 .
.

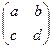 = аналогично,
= аналогично, 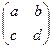 .
.
Матрица  называется единичной матрицей. При этом выполняется
называется единичной матрицей. При этом выполняется 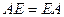 .
.
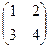
 =
= 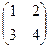 и
и 
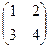 =
= 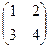 .
.
(Аналог среди матриц первого порядка: число 1). Итак,  .
.
ПРАКТИКА 2.
Задача 17. Доказать, что во множестве матриц 2 порядка существует обратный элемент по умножению. Указание. Для матрицы 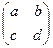 рассмотреть
рассмотреть 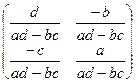 .
.
Примечание. 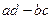 - определитель матрицы. Мы выведем формулу вычисления обратной матрицы позже, в линейной алгебре.
- определитель матрицы. Мы выведем формулу вычисления обратной матрицы позже, в линейной алгебре.
Решение. Проверим:
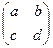
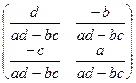 =
= 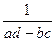
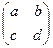
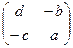 =
=
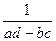
 =
=  .
.
Задача 18. Доказать, что на множестве всех векторов трёхмерного пространства с операцией векторного умножения не существует нейтральный элемент.
Решение. Образ векторного произведения 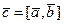 перпендикулярен умножаемым векторам:
перпендикулярен умножаемым векторам: 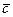 ┴
┴ 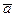 ,
, 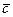 ┴
┴ 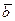 . Предположим, что существует нейтральный элемент относительно данной операции, тогда
. Предположим, что существует нейтральный элемент относительно данной операции, тогда 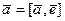 для всякого вектора
для всякого вектора 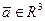 , откуда следует
, откуда следует 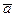 ┴
┴ 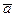 , что невозможно. Поэтому не существует вектор
, что невозможно. Поэтому не существует вектор  , при умножении на который всякий вектор
, при умножении на который всякий вектор 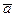 отображался бы в вектор
отображался бы в вектор 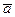 .
.
Задача 19. Доказать, что бинарная операция 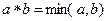 на множестве чисел
на множестве чисел 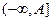 является коммутативной и ассоциативной; найти нейтральный элемент.
является коммутативной и ассоциативной; найти нейтральный элемент.
Решение. Очевидно, что  . Ассоциативность:
. Ассоциативность: 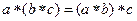 выполнена так как при любой расстановке скобок результатом будет минимальное из трёх заданных чисел. Нейтральным элементом является число
выполнена так как при любой расстановке скобок результатом будет минимальное из трёх заданных чисел. Нейтральным элементом является число 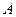 , так как для любого
, так как для любого  верно
верно  , значит
, значит  .
.
Замечание. Для рассмотренной операции, задаваемой на множестве, неограниченном сверху, а также ограниченном, но не содержащем свою точную верхнюю грань, например 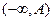 , нейтрального элемента не существует.
, нейтрального элемента не существует.
Аналогично для множества 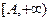 определяется бинарная алгебраическая операция
определяется бинарная алгебраическая операция 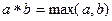 , причём нейтральным элементом является число
, причём нейтральным элементом является число 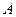 .
.
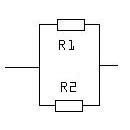
Задача 20. Доказать, что множество всех сопротивлений (резисторов) образует коммутативный и ассоциативный группоид относительно операции параллельного соединения.
Решение.
Известно, что если сопротивления R1 и R2 соединить параллельно, то сопротивление получившегося элемента электрической цепи вычисляется по формуле  , т.е.
, т.е.  .
.
Можно поставить в соответствие множество сопротивлений и множество неотрицательных чисел. Вводя на множестве неотрицательных действительных чисел [0, ∞) бинарную операцию  , докажем, что введённая операция будет коммутативной и ассоциативной.
, докажем, что введённая операция будет коммутативной и ассоциативной.
Коммутативность: 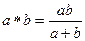 =
= 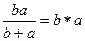 .
.
Ассоциативность следует из равенств:
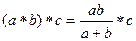 =
= 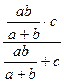 =
= 
= 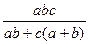 =
=  .
.
С другой стороны,
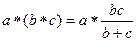 =
=  =
= 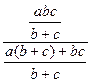
=  .
.
Таким образом, 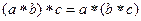 .
.
При этом 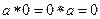 ,
, 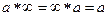 . Последнее следует из того, что
. Последнее следует из того, что 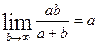 . Чтобы вычислить такой предел, можно сократить на
. Чтобы вычислить такой предел, можно сократить на  :
:  .
.
Нейтральным элементом относительно операции параллельного соединения будет участок электрической цепи, обладающий нулевой проводимостью, то есть изолятор с бесконечным сопротивлением. Тогда в предельном случае при 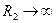 получаем
получаем 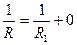 .
.
Задача 21. Доказать, что множество функций
 ,
, 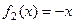 ,
, 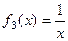 ,
, 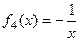
образует группоид относительно операции композиции.
Решение.
Проверим, что композиции приводят к функциям такого же вида, как указанные 4.
Во-первых очевидно, что 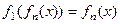 ,
, 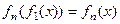 .
.
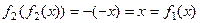 .
. 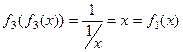 .
.
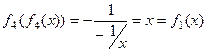 .
.
 .
.  .
.
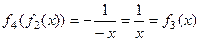 .
.  .
.
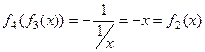 .
. 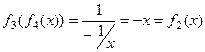 .
.
Таблица:
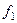
| 
| 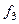
| 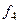
| |
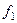
| 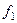
| 
| 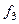
| 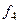
|

| 
| 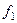
| 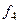
| 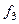
|
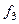
| 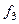
| 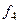
| 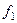
| 
|
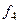
| 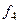
| 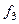
| 
| 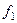
|
Нейтральный элемент 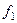 . Для каждого есть и обратный элемент (в каждой строке присутствует
. Для каждого есть и обратный элемент (в каждой строке присутствует 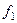 ).
).
На самом деле, это множество функций образует не только группоид, но и группу (только для этого надо проверять ещё и ассоциативность).
Множество  ,
, 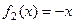 её подгруппа.
её подгруппа.
А вот  ,
, 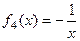 не подгруппа (не содержит нейтральный элемент).
не подгруппа (не содержит нейтральный элемент).
.
Группы
Задача 22. Является ли группой следующий группоид:
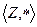 , где
, где 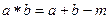 . (
. (  ).
).
Решение. Во-первых, является группоидом, так как  замкнуто относительно этой операции.
замкнуто относительно этой операции.
Проверка того факта, что полугруппа (ассоциативность).
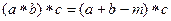 =
= 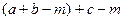 =
=  .
.
 =
=  =
=  .
.
Ассоциативность есть.
Ищем нейтральный элемент.
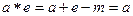
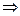
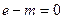
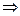
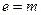 .
.
Ищем обратный элемент.
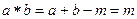 (так как
(так как 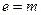 )
) 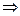

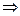
 .
.
Итак, это множество образует группу относительно данной операции.
Задача 23. Является ли группой следующий группоид: 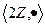 .
.
Решение. Множество всех чётных чисел с операцией умножения. Группоидом является, т.к. произведение чётных снова чётно. Полугруппой тоже (ассоциативность по умножению очевидна).
Нейтральный элемент по умножению 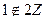 . Обратный элемент дробный, не принадлежит ни
. Обратный элемент дробный, не принадлежит ни 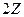 , ни даже
, ни даже  . Вывод: группу не образует.
. Вывод: группу не образует.
Определение. Группы  называются изоморфными, если существует взаимно-однозначное отображение
называются изоморфными, если существует взаимно-однозначное отображение 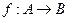 , такое, что для любых элементов
, такое, что для любых элементов 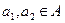 выполняется
выполняется 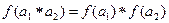 .
.
Например, поворот плоскости относительно суммирования векторов – изоморфное отображение: суммирование векторов либо до, либо после поворота приводит к одному и тому же результату.
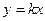 сложить можно как до, так и после умножения на коэффициент:
сложить можно как до, так и после умножения на коэффициент: 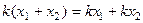 .
.
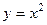 не изоморфное, так как
не изоморфное, так как 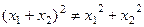 .
.
Пример: группа движений и симметрий правильных n-угольников. Для правильного n-угольника, группа всех поворотов и симметрий состоит из 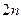 элементов. В группе подстановок ей изоморфна некоторая подгруппа, состоящая из
элементов. В группе подстановок ей изоморфна некоторая подгруппа, состоящая из 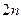 элементов.
элементов.
Задача 24. Найти подгруппу в группе подстановок порядка 4, изоморфную группе движений квадрата.
Решение. Заметим, что не каждая подстановка соответствует какому-то вращению или зеркальному отражению квадрата, например, 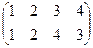 .
.
Всего существует 4!=24 подстановки 4 порядка. В то же время, для движений квадрата всего 8 вариантов: 4 поворота (на углы 0,90,180,270) и 4 зеркальных отражений.
Сделаем все повороты на чертеже по порядку (по часовой стрелке).
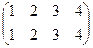 ,
, 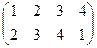 ,
, 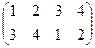 ,
, 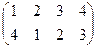 ,
,
Зеркальные отражения:
 ,
, 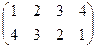 ,
, 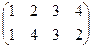 ,
,  .
.
две последних - относительно диагоналей, там то 1,3 то 2,4 остаются на месте.
Любое зеркальное отражение является композицией первого зеркального отражения (относительно вертикальной линии) а именно  и некоторого поворота.
и некоторого поворота.
Например, отражение 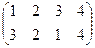 относительно диагонали, сохраняющее 2 и 4 на месте, это композиция:
относительно диагонали, сохраняющее 2 и 4 на месте, это композиция:

Эти 8 подстановок образуют подгруппу, изоморфную группе движений квадрата.
Задача 25. Найти подгруппу в группе подстановок порядка 4, изоморфную группе движений ромба.

Решение.
Во-первых, повороты на 00 и 1800:
 и
и 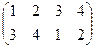
Зеркальные отражения относительно диагоналей:
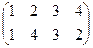 и
и 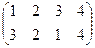 (то 1 и 3, то 2 и 4 сохраняются).
(то 1 и 3, то 2 и 4 сохраняются).
Причём, каждое из зеркальных отражений - это композиция другого отражения и поворота на 180 градусов.
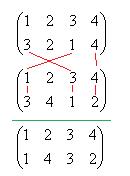
Обратный к каждому элемент это он сам. Если поменять 2 строки в каждой из таких подстановок и снова расположить по порядку, то исходная и получится.
Задача 26. Доказать, что множество всевозможных поворотов и симметрий тетраэдра образует группу, изоморфную группе подстановок 4-го порядка.
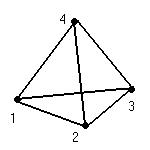
Решение. Каждое преобразование симметрии, при котором меняются местами две вершины, соответствует некоторой подстановке, меняющей местами два элемента (такая подстановка называется транспозицией).
Любая подстановка может быть получена с помощью транспозиций, поэтому любое преобразования тетраэдра может быть получено с помощью последовательного выполнения нескольких отображений симметрии.
п. 27. Комплексные числа и действия над ними.
Система действительных чисел является неполной, так как не содержит корни некоторых многочленов, например  . Если квадратичное уравнение
. Если квадратичное уравнение 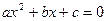 имеет отрицательный дискриминант, то есть
имеет отрицательный дискриминант, то есть 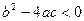 , то на действительной оси нет ни одного корня. Введено абстрактное понятие «мнимая единица»
, то на действительной оси нет ни одного корня. Введено абстрактное понятие «мнимая единица» 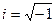 обозначающая «квадратный корень из минус 1». При этом получается
обозначающая «квадратный корень из минус 1». При этом получается 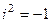 .
.
Геометрическая интерпретация. На плоскости, горизонтальная ось отождествляется со множеством действительных чисел, а мнимая ось, содержащая  , перпендикулярна оси действительных чисел.
, перпендикулярна оси действительных чисел.

Каждой точке на плоскости с координатами  можно поставить в соответствие комплексное число, состоящее из действительной и мнимой части:
можно поставить в соответствие комплексное число, состоящее из действительной и мнимой части: 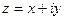 . Проекция на действительную и мнимую ось называются действительной частью и мнимой частью комплексного числа.
. Проекция на действительную и мнимую ось называются действительной частью и мнимой частью комплексного числа.  ,
, 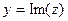 .
.
Если 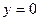 , то число
, то число 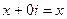 это обычное действительное число.
это обычное действительное число.
Сложение и вычитание комплексных чисел определяется покоординатно, как для обычных векторов в плоскости.
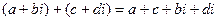 =
=  .
.
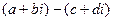 =
=  .
.
Умножение.
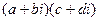 =
= 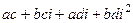 , учитывая тот факт, что
, учитывая тот факт, что 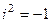 ,
,
получаем 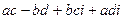 =
= 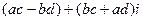 .
.
Таким образом, после раскрытия скобок, надо просто учесть 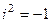 и привести подобные.
и привести подобные.
Пример. 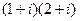 =
= 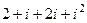 =
= 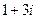 .
.
Определение. число 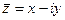 называется сопряжённым к
называется сопряжённым к 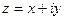 .
.
Умножим два взаимно сопряжённых комплексных числа:
 =
= 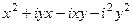 =
= 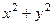 , получилось действительное число. Мы заметили, что при умножении на сопряжённое мнимая часть станет 0.
, получилось действительное число. Мы заметили, что при умножении на сопряжённое мнимая часть станет 0.
Существует обратный элемент по умножению:
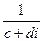 =
= 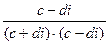 =
=  =
=  .
.
Таким образом, множество комплексных чисел (за исключением 0) образует группу по умножению.
Поиск корней многочлена с отрицательным дискриминантом.
Пример 28. Найти корни уравнения  .
.
Решение. 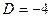 ,
,  =
= 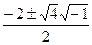 =
= 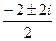 =
= 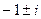 .
.
Ответ. 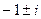 .
.
Кстати, как видно, получаются именно 2 взаимно сопряжённых корня.
Проверка. Подставим, например, 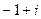 в уравнение.
в уравнение.
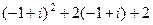 =
=  =
= 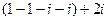 =
= 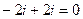 .
.
Задача 29. Доказать, что группа, состоящая из 3 элементов, является коммутативной.
Решение. Так как 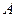 - группа, то она должна содержать единицу относительно операции, действующей в данной группе. Тогда группа состоит из элементов 1,
- группа, то она должна содержать единицу относительно операции, действующей в данной группе. Тогда группа состоит из элементов 1,  ,
,  . Рассмотрим всевозможные 9 произведений. Произведение любого элемента на 1 равно исходному элементу. Исследуем произведения
. Рассмотрим всевозможные 9 произведений. Произведение любого элемента на 1 равно исходному элементу. Исследуем произведения 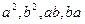 .
.
| 1 | 
| 
| |
| 1 | 1 | 
| 
|

| 
| 
| 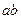
|

| 
| 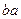
| 
|
Для каждого элемента должен существовать обратный, поэтому в каждой строке и каждом столбце должен быть единичный элемент. Таким образом,  =1 или
=1 или 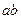 =1. Пусть сам элемент
=1. Пусть сам элемент  является обратным к
является обратным к  , то есть
, то есть  =1. Тогда
=1. Тогда 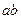
 , иначе для элемента
, иначе для элемента  существовало бы два различных обратных, а это невозможно. Также при этом не может быть
существовало бы два различных обратных, а это невозможно. Также при этом не может быть 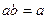 .Ведь тогда элемент
.Ведь тогда элемент  являлся бы нейтральным при умножении на
являлся бы нейтральным при умножении на  , но нейтральный элемент единственный (было доказано в лекциях), и
, но нейтральный элемент единственный (было доказано в лекциях), и  . По этой же причине невозможно
. По этой же причине невозможно 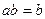 . Следовательно,
. Следовательно, 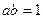 , это означает, что элемент
, это означает, что элемент  - обратный к элементу
- обратный к элементу  в этой группе. Отсюда следует
в этой группе. Отсюда следует 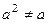 , иначе
, иначе  также был бы обратным к
также был бы обратным к  , но это невозможно, так как обратный элемент единственный. Остаётся только одна возможность:
, но это невозможно, так как обратный элемент единственный. Остаётся только одна возможность: 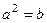 . Аналогичными рассуждениями доказывается, что
. Аналогичными рассуждениями доказывается, что 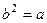 . Итак, умножение в группе из 3 элементов можно представить следующей таблицей:
. Итак, умножение в группе из 3 элементов можно представить следующей таблицей:
| 1 | 
| 
| |
| 1 | 1 | 
| 
|

| 
| 
| 1 |

| 
| 1 | 
|
Так как 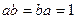 , то группа коммутативная (абелева).
, то группа коммутативная (абелева).
ПРАКТИКА 3.
Дата добавления: 2020-12-22; просмотров: 70; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
