Односторонние пределы конечны и равны.
Конспект урока математики
Дата 13..11.20; 24.11.20
Курс 2
Группа 4
Тема урока: «Исследование функции на непрерывность»
Урок № 27-28
Форма работы: индивидуальная, дистанционное обучение.
Тип урока: урок изучения нового материала.
Цель урока: получить понятие исследования функции на непрерывность
Изучаемая литература: Математика : алгебра и начала математического анализа, геометрия. Алгебра и начала математического анализа.
10-11 классы: учеб.для общеобразоват.организаций: базовый и углубл.уровени./Ш.А.Алимов, Ю.М.Колягин, М.В.Ткачева и др.- 5 изд.- М.: Просвещение , 2018г
Интернет ресурсы. Математика в открытом колледже http://www.mathematics.ru
Ход занятия :
Организационный этап. Мотивационный модуль
Ребята, сегодня, вы рассмотрите материал по теме : «Исследование функции на непрерывность.».
Основная часть. Объясняющий модуль.
План изучения
1. Повторение определения непрерывной функции в точке и на промежутке.
2. План исследования функций.
3. Решение примеров на исследование функций
Определение 1
Функция f(x)f(x)является непрерывной в точке x0, если предел слева равен пределу справа и совпадает со значением функции в точке x0, т.е.: limx→x0−0f(x)=limx→x0+0f(x)=f(x0)
Определение 2
Функция имеет устранимый разрыв первого рода в точке х0, когда пределы справа и слева равны, но не равны значению функции в точке, т.е.:
|
|
|
limx→x0−0f(x)=limx→x0+0f(x)≠f(x0)
Определение 3
Функция имеет неустранимый разрыв первого рода в точке х0, когда пределы справа и слева не являются равными, т.е.: limx→x0−0f(x)≠limx→x0+0f(x)limx→x0-0f(x)≠limx→x0+0f(x). Точка х0 здесь – точка скачка функции.
Определение 4
Функция имеет разрыв второго рода в точке х0, когда какой-либо из пределов слева limx→x0−0f(x)limx→x0-0f(x) или справа limx→x0+0f(x)limx→x0+0f(x) не существует или бесконечен.
Для исследования функции на непрерывность необходимо:
1. Найти область определения функции;
2. Рассмотреть односторонние пределы в точках, где функция не существует; если функция кусочная, то рассмотреть односторонние пределы в точках «склейки»;
3. Исследовать функцию на бесконечности;
4. Построить эскиз графика функции.
Для классификации точек разрыва функции 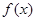 можно пользоваться таблицей, приведенной ниже.
можно пользоваться таблицей, приведенной ниже.
Пусть 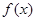 – заданная функция,
– заданная функция, 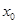 – исследуемая точка,
– исследуемая точка, 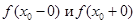 – соответственно левый и правый пределы функции.
– соответственно левый и правый пределы функции.
| Тип разрыва | Условия |
| Функция непрерывна | 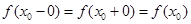
|
| Устранимый разрыв | 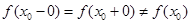
|
| Разрыв первого рода (скачок) | 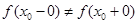 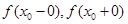 – конечны – конечны
|
| Разрыв второго рода | 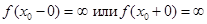
|
4. Закрепление темы. Тренировочный модуль.
|
|
|
Пример 1
Исследовать функцию 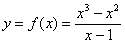 на непрерывность. Определить характер разрывов функции, если они существуют. Выполнить чертёж.
на непрерывность. Определить характер разрывов функции, если они существуют. Выполнить чертёж.
Решение:
1) В точке 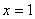 , функция не определена.
, функция не определена.
2) Вычислим односторонние пределы:
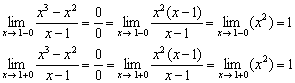
Односторонние пределы конечны и равны.
Таким образом, в точке 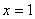 функция терпит устранимый разрыв.
функция терпит устранимый разрыв.
Как выглядит график данной функции?
Проведем упрощение 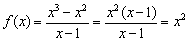 , и вроде бы получается обычная парабола. НО исходная функция не определена в точке
, и вроде бы получается обычная парабола. НО исходная функция не определена в точке 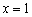 , поэтому обязательна следующая оговорка:
, поэтому обязательна следующая оговорка:
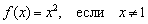
Выполним чертёж:
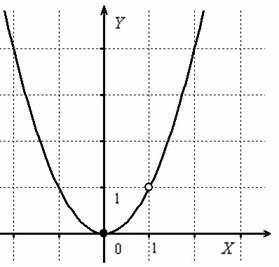
Ответ: функция непрерывна на всей числовой прямой кроме точки 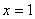 , в которой она терпит устранимый разрыв.
, в которой она терпит устранимый разрыв.
Пример 2
Исследовать функцию 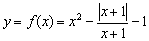 на непрерывность. Определить характер разрывов функции, если они существуют. Выполнить чертёж.
на непрерывность. Определить характер разрывов функции, если они существуют. Выполнить чертёж.
Решение: Поскольку модуль неотрицателен, то он раскрывается следующим образом: 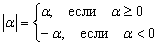 , где «альфа» – некоторое выражение. В данном случае
, где «альфа» – некоторое выражение. В данном случае 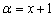 , и наша функция должна расписаться кусочным образом:
, и наша функция должна расписаться кусочным образом:
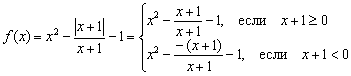
Сократим дроби на 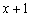 . Исходная функция не определена в точке
. Исходная функция не определена в точке 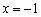 , так как знаменатель обращается в ноль. Поэтому
, так как знаменатель обращается в ноль. Поэтому 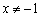 , и первое неравенство
, и первое неравенство 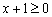 сделать строгим:
сделать строгим:
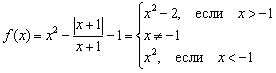
Выполним чертёж. В соответствии с нашими выкладками, слева от точки 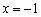 необходимо начертить фрагмент параболы
необходимо начертить фрагмент параболы 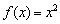 (синий цвет), а справа – кусок параболы
(синий цвет), а справа – кусок параболы 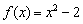 (красный цвет), при этом функция не определена в самой точке
(красный цвет), при этом функция не определена в самой точке 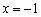 :
:
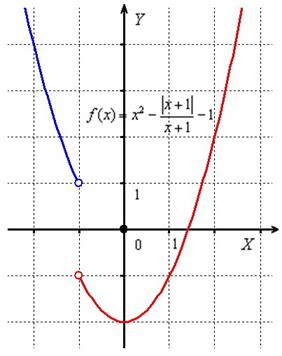
Ответ: функция непрерывна на всей числовой прямой кроме точки 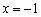 , в которой она терпит разрыв первого рода со скачком.
, в которой она терпит разрыв первого рода со скачком.
|
|
|
Рассмотрим примеры кусочных функций.
Пример 3. 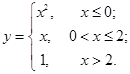
Функции 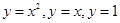 являются непрерывными всюду, кроме, может быть, точек «склейки», то есть в
являются непрерывными всюду, кроме, может быть, точек «склейки», то есть в 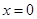 ,
, 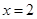 . Исследуем поведение функции в окрестности этих точек:
. Исследуем поведение функции в окрестности этих точек:

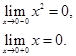
При 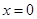 функция
функция 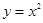 определена и равна нулю, а функция
определена и равна нулю, а функция 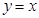 в эту точку не заходит по условию.
в эту точку не заходит по условию.
· Функция 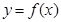 называется непрерывной в
называется непрерывной в 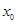 , если ее левосторонний и правосторонний пределы существуют, между собой равны и равны значению функции в этой точке, то есть
, если ее левосторонний и правосторонний пределы существуют, между собой равны и равны значению функции в этой точке, то есть 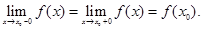
Следовательно, точка x= 0 является точкой непрерывности функции.
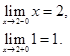
Делаем вывод, что точка x= 2 является точкой разрыва первого рода и непрерывна слева (по условию).
Строим график склеенной функции:
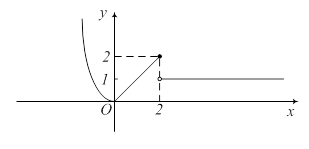
Домашнее задание : написать конспект по теме урока.
Дата добавления: 2020-12-22; просмотров: 121; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
