Интегрирование по частям. Примеры решений
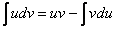– формула интегрирования по.
По частям берутся интегралы следующих видов:
1) 
, 
, 
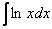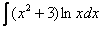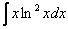– логарифм, логарифм, умноженный на какой-нибудь многочлен.
2) 
, 
– экспоненциальная функция, умноженная на какой-нибудь многочлен. Сюда же можно отнести интегралы вроде 
– показательная функция, умноженная на многочлен.
3) 
, 
, 
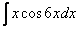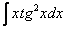– тригонометрические функции, умноженные на какой-нибудь многочлен.
4) 
, 
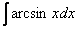– обратные тригонометрические функции, умноженные на какой-нибудь многочлен.
Также по частям берутся некоторые дроби, соответствующие примеры мы тоже подробно рассмотрим.
Интегралы от логарифмов
Пример 1 Найти неопределенный интеграл. 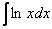Решаем: 
.
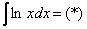Используем формулу интегрирования по частям: 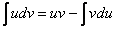Формула применяется слева направо. Смотрим на левую часть: 
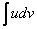. В нашем примере 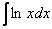что-то нужно обозначить за 
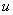, а что-то за 
. В интегралах рассматриваемого типа за 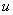всегда обозначается логарифм.
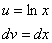То есть, за 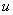мы обозначили логарифм, а за – оставшуюся часть подынтегрального выражения.
Следующий этап: находим дифференциал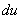 
: 
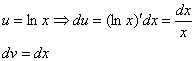
Теперь находим функцию 
. Для того чтобы найти функцию необходимо проинтегрировать правую часть нижнего равенства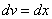 
: 
Теперь открываем наше решение и конструируем правую часть формулы: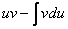 
. 
Единственный момент, в произведении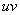 
сразу переставили местам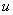и и , так как множитель 
принято записывать перед логарифмом. Как видите, применение формулы интегрирования по частям, по сути дела, свело наше решение к двум простым интегралам.
|
|
|
Обратите внимание, что в ряде случаев сразу после применения формулы, под оставшимся интегралом обязательно проводится упрощение – в рассматриваемом примере мы сократили подынтегральное выражение на «икс».
Выполним проверку. Для этого нужно взять производную от ответа:
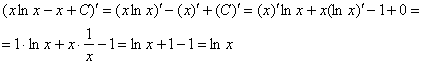
Получена исходная подынтегральная функция, значит, интеграл решён правильно.
Формула интегрирования по частям 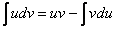и формула 
– это два взаимно обратных правила.
Пример 2 Найти неопределенный интеграл. 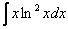Решаем. 
Как уже говорилось, за 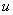необходимо обозначить логарифм (то, что он в степени – значения не имеет). За обозначаем оставшуюся часть подынтегрального выражения.
Записываем в столбик: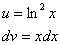 
Сначала находим дифференциал :
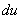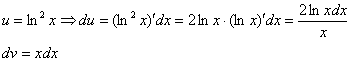
Здесь использовано правило дифференцирования сложной функции 
. Теперь находим функцию , для этого интегрируем правую часть нижнего равенства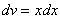 
:
Теперь всё готово для применения формулы .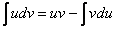 
Под интегралом у нас снова многочлен на логарифм! Поэтому решение опять прерывается и правило интегрирования по частям применяется второй раз. Не забываем, что за 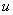в похожих ситуациях всегда обозначается логарифм.
|
|
|
Хорошо бы, если к данному моменту простейшие интегралы и производные Вы умели находить устно.
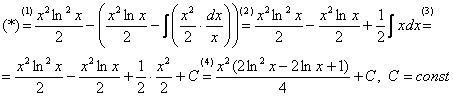
(1) Не путаемся в знаках! Очень часто здесь теряют минус, также обратите внимание, что минус относится ко всей скобке 
, и эти скобки нужно корректно раскрыть.
(2) Раскрываем скобки. Последний интеграл упрощаем.
(3) Берем последний интеграл.
(4) «Причесываем» ответ.
Необходимость дважды (а то и трижды) применять правило интегрирования по частям возникает не так уж и редко.
Дата добавления: 2020-12-22; просмотров: 72; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!