Метод замены переменной в неопределенном интеграле
Методы интегрирования Подведение функции под знак дифференциала
Технически метод замены переменной в неопределенном интеграле реализуется двумя способами:
– Подведение функции под знак дифференциала;
– Собственно замена переменной.
По сути дела, это одно и то же, но оформление решения выглядит по-разному.
Пример 1Найти неопределенный интеграл. Выполнить проверку.
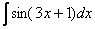Смотрим на таблицу интегралов и находим похожую формулу: 
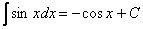. Но проблема заключается в том, что у нас под синусом не просто буковка «икс», а сложное выражение. Что делать? Подводим функцию 
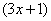под знак дифференциала:
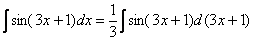Раскрывая дифференциал, легко проверить, что:
Фактически 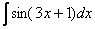и 
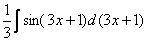– это запись одного и того же.
А как мы пришли к мысли, что на первом шаге нужно записать наш интеграл именно так: 
? Почему так, а не иначе?
Формула 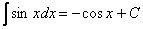(и все другие табличные формулы) справедливы и применимы НЕ ТОЛЬКО для переменной 
, но и для любого сложного выражения ЛИШЬ БЫ АРГУМЕНТ ФУНКЦИИ (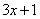 
– в нашем примере) И ВЫРАЖЕНИЕ ПОД ЗНАКОМ ДИФФЕРЕНЦИАЛА БЫЛИ ОДИНАКОВЫМИ.
Рассуждаем при решении примерно так: «надо решить интеграл 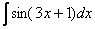. Я посмотрел в таблицу и нашел похожую формулу 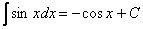. Но у меня сложный аргумент 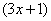и формулой я сразу воспользоваться не могу. Однако если мне удастся получить 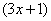и под знаком дифференциала, то всё будет нормально. Если записать 
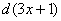, тогда 
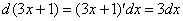. Но в исходном интеграле 
множителя-тройки нет, поэтому, чтобы подынтегральная функция не изменилась, надо ее домножить на 
»:
|
|
|
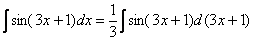
Теперь можно пользоваться табличной формулой :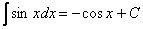
Единственное отличие, у нас не буква «икс», а сложное выражение .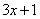
Выполним проверку. Открываем таблицу производных и дифференцируем ответ:
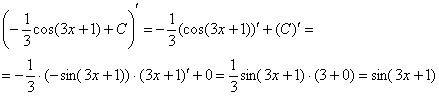
Получена исходная подынтегральная функция, значит, интеграл найден правильно.
Обратите внимание, что в ходе проверки мы использовали правило дифференцирования сложной функции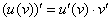 
. По сути дела подведение функции под знак дифференциала и 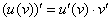– это два взаимно обратных правила.
Пример 2Найти неопределенный интеграл. Выполнить проверку.
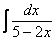
Анализируем подынтегральную функцию. Здесь у нас дробь, причем в знаменателе линейная функция (с «иксом» в первой степени). Смотрим в таблицу интегралов и находим наиболее похожую вещь: 
.
Подводим функцию 
под знак дифференциала: 
Если трудно сразу сообразить, на какую дробь нужно домножать, можно быстренько на черновике раскрыть дифференциал: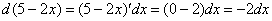 
. И так, получается 
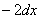, значит, чтобы ничего не изменилось, надо домножить интеграл на 
.
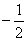Далее используем табличную формулу :
Проверка: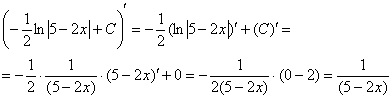 
Получена исходная подынтегральная функция, значит, интеграл найден правильно.
Пример 3 Найти неопределенный интеграл. Выполнить проверку.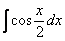 
|
|
|
Решение: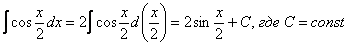 
Пример 4 Найти неопределенный интеграл. Выполнить проверку.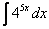 
Решение: 
Еще несколько примеров:
а) 
б)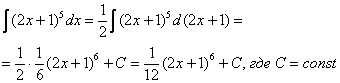 
в) 
г) 
д)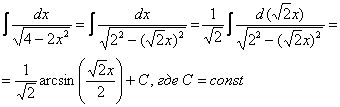 
И так далее.
Когда в линейной функции переменная входит с единичным коэффициентом, например:
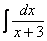длинным решением часто пренебрегают и сразу записывают, что 
.
Метод замены переменной в неопределенном интеграле
Пример 5 Найти неопределенный интеграл. 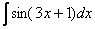(см. пример 1)
Идея метода замены состоит в том, чтобы сложное выражение (или некоторую функцию) заменить одной буквой. В данном случае напрашивается: 
Итак: 
Но при замене у нас остаётся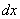 
! Если осуществляется переход к новой переменной 
, то в новом интеграле всё должно быть выражено через букву . Значит 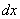нужно превратить в некоторое выражение, которое зависит только от .
После того, как подобрали замену, в данном примере, , нам нужно найти дифференциал 
. Так как , то 
: 
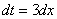
Теперь по правилам пропорции выражаем нужный нам :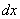 
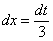
В итоге: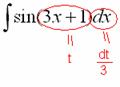 
Таким образом: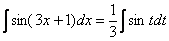 
А это уже табличный интеграл 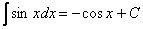(таблица интегралов, естественно, справедлива и для переменной ).
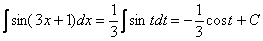В заключении осталось провести обратную замену. Вспоминаем, что . 
А теперь самое время вспомнить первый способ решения:
|
|
|
В чем разница? Принципиальной разницы нет. Это фактически одно и то же. Но с точки зрения оформления задания метод подведения функции под знак дифференциала – гораздо короче.
Возникает вопрос. Если первый способ короче, то зачем тогда использовать метод замены? Дело в том, что для ряда интегралов не так-то просто «подогнать» функцию под знак дифференциала.
Пример 6 Найти неопределенный интеграл(НИ).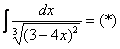 
Проведем замену: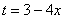 
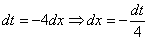
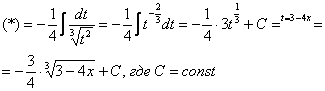
Как видите, в результате замены исходный интеграл значительно упростился – свёлся к обычной степенной функции. Это и есть цель замены – упростить интеграл.
Пример 7Найти НИ. 
Замена: 
Пример 8 Найти неопределенный интеграл. 
основная предпосылка использования метода замены переменной: в подынтегральном выражении должна находиться некоторая функция 
и её производная 
: 
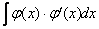(функции , могут быть и не в произведении)
В рассматриваемом примере замечаем, что степень числителя на единицу меньше степени знаменателя. В таблице производных находим формулу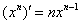 
, которая как раз понижает степень на единицу. А, значит, если обозначить за знаменатель, то велики шансы, что числитель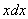 
превратится во что-нибудь хорошее.
|
|
|
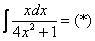Замена: 
Следует отметить, что для дробей вроде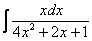 
, 
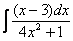такой фокус уже не пройдет (точнее говоря, применить нужно будет не только прием замены). Вот еще пара типовых примеров для самостоятельного решения из той же оперы:
Пример 9 Найти неопределенный интеграл.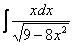 
Проведем замену: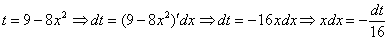 
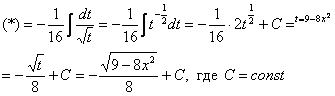
Пример 10 Найти неопределенный интеграл. 
Проведем замену: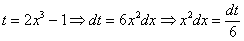 
Пример 11 Найти неопределенный интеграл.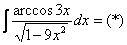 
Смотрим в таблицу производных и находим наш арккосинус: 
. В подынтегральном выражении находится арккосинус и нечто похожее на его производную.
Общее правило: За обозначаем саму функцию (а не её производную).
В данном случае: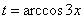 
. Осталось выяснить, во что превратится оставшаяся часть подынтегрального выражения 
. В этом примере нахождение рассмотрим подробно поскольку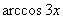 
– сложная функция.
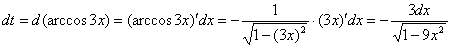Или короче: 
По правилу пропорции выражаем нужный нам остаток: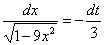 
Таким образом: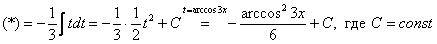 
Дата добавления: 2020-12-22; просмотров: 64; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!