Свойство пересекающихся хорд.
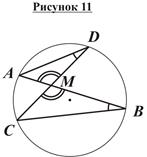
Свойство пересекающихся хорд: Если две хорды окружности пересекаются, то произведение отрезков одной хорды равно произведению отрезков второй хорды (рисунок 11).
Дано:
окружность (O; R);
A, B, C, D Ì (O; R);
AB∩CD = M.
Доказать: AM∙MB = CM∙MD.
Доказательство:
1. По теореме о вписанном угле,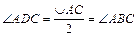 
; ÐAMD = ÐCMB, как вертикальные; Þ по первому признаку подобия треугольников, ΔAMD ~ ΔCMB.
2. ΔAMD ~ ΔCMB; Þ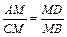 
, Þ AM∙MB = CM∙MD. #
Угол между касательной и хордой.
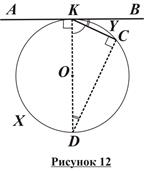Теорема об угле между касательной и хордой: Угол между касательной к окружности и хордой с концом в точке касания измеряется половиной дуги, которую стягивает эта хорда, заключенной внутри угла (рисунок 12).
Дано:
окружность (O; R);
AB ∩ (O; R) = !K;
X, C, Y Ì (O; R);
X Î ÐAKC; Y Î ÐBKC.
Доказать : 
;
.
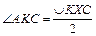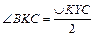Доказательство:
1. Пусть ÐAKC тупой; тогда ÐBKC = 180° – ÐAKC – острый. Проведем диаметр KD и соединим точки C и D. Тогда по свойству касательной к окружности, ÐAKD = ÐBKD = 90°, а по следствию из теоремы о вписанном угле, ÐKCD = 90°.
2. Из пункта 1,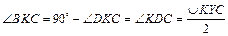 
, т.к. ÐKDC – вписанный.
3. 
. #
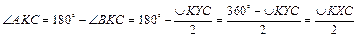Касательная и секущая, проведенные к окружности из одной точки. Секущие, проведенные к окружности из одной точки.
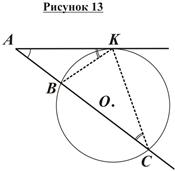
Пусть из точки A проведен луч, пересекающий окружность в точках B и C, причем точка B лежит между точками A и C (рисунок 13). Тогда отрезок AC принято называть отрезком секущей; отрезок AB – внешней частью отрезка секущей, а отрезок BC – его внутренней частью. Если к окружности из точки A проведены касательная AK и секущая ABC, то отрезки AK, AB и AC связаны соотношением, которое устанавливает следующая теорема:
|
|
|
Свойство касательной и секущей, проведенных к окружности из одной точки: Если к окружности из одной точки проведены касательная и секущая, то квадрат отрезка касательной равен произведению отрезка секущей на его внешнюю часть (рисунок 13).
Дано:
окружность (O; R);
AK ∩ (O; R) = !K;
B, C Ì (O; R); B Î AC.
Доказать: AK2 = AB∙AC.
Доказательство:
1. Соединим точки B, K и C. Тогда по теореме о вписанном угле,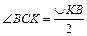 
, а по теореме об угле между касательной и хордой, 
.
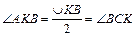2. ΔAKB ~ ΔACK по двум углам (ÐA – общий, ÐAKB = ÐBCK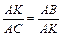); Þ 
, Þ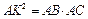 
. #
Следствие (свойство секущих, проведенных к окружности из одной точки): Если к окружности из одной точки проведены две секущие, то произведение отрезка первой секущей на его внешнюю часть равен произведению отрезка второй секущей на его внешнюю часть (рисунок 14).
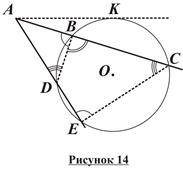Дано:
окружность (O; R);
B, C, D, E Ì (O; R);
B Î AC; D Î AE.
Доказать: AB∙AC = AD∙AE.
Доказательство:
Проведем из точки A касательную AK к окружности. Тогда по доказанной теореме,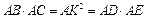 
. #
|
|
|
Замечание: Если из точки A к окружности проведены секущие ABC и ADE, то ΔABD ~ ΔAEC (рисунок 14). Доказать это можно одним из двух способов:
1. AB∙AC = AD∙AE, Þ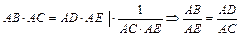 
. Тогда ΔABD ~ ΔAEC по двум сторонам и углу между ними (ÐA – общий). #
2. 
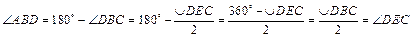, Þ ΔABD ~ ΔAEC по двум углам (ÐA – общий). #
Дата добавления: 2020-11-29; просмотров: 530; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!