Градусная мера дуги окружности. Центральный и вписанный углы.
VIII класс: Тема 6. Измерение углов и отрезков, связанных с окружностью.
Определение окружности и ее элементов. Взаимное расположение прямой и окружности.
Окружностью называется фигура, состоящая из всех точек, равноудаленных от данной точки – центра окружности (рисунок 1). Расстояние от точки окружности до ее центра называется радиусом окружности. Также радиусом окружности называют отрезок, соединяющий любую точку окружности с ее центром. Окружность с центром в точке O радиусом R обозначается (O; R).
Хордой окружности называется отрезок, соединяющий любые две ее точки. Диаметром окружности называется хорда окружности, содержащая ее центр.
Замечание 1: Длина диаметра равна двум радиусам окружности.
Дугой окружности называют каждую из двух ее частей, на которые она разбивается любыми двумя точками. При этом говорят, что хорда с концами в этих точках стягивает соответствующие дуги. Дуга AB обозначается 
.
Замечание 2: Всякая хорда окружности стягивает две дуги, которые называют дополнительными.
Дуга, стягиваемая диаметром окружности, называется полуокружностью.
Прямая и окружность могут иметь 0, 1 или 2 общие точки (рисунок 1), что определяется расстоянием от центра окружности до прямой. Если расстояние от центра окружности до прямой меньше радиуса окружности, то прямая пересекает окружность в двух точках; если расстояние больше радиуса, то прямая и окружность не имеют общих точек; наконец, если расстояние от центра окружности до прямой равно радиусу окружности, то прямая и окружность имеют единственную общую точку.
|
|
|
Прямая, пересекающая окружность в двух точках, называется секущей к окружности. Прямая, имеющая единственную общую точку с окружностью, называется касательной к окружности; при этом общую точку прямой и окружности называют точкой касания.
Свойство касательной к окружности: Касательная к окружности перпендикулярна радиусу, проведенному в точку касания (на рисунке 2 прямая l касается окружности (O; R) в точке K, Þ OK ^ l).
Справедлива также обратная теорема – признак касательной к окружности: Если прямая имеет общую точку с окружностью и перпендикулярна радиусу, проведенному в эту точку, то она не имеет других общих точек с окружностью, то есть является касательной к ней.
Сформулированные теоремы доказываются от противного; мы примем их без доказательства.
Докажем свойство касательных, проведенных к окружности из одной точки: Отрезки касательных, проведенных к окружности из одной точки, равны и составляют равные углы с прямой, проходящей через эту точку и центр окружности (рисунок 3).
Дано:
|
|
|
окружность (O; R);
XA Ç (O; R) = !A;
XB Ç (O; R) = !B.
Доказать: XA = XB;
ÐAXO = ÐBXO.
Доказательство:
1. Проведем радиусы OA и OB в точки касания. По свойству касательной к окружности ÐXAO = ÐXBO = 90°.
2. 
ΔXAO = ΔXBO по гипотенузе и катету (XO – общая, AO = BO = R), Þ XA = XB; ÐAXO = ÐBXO. #
Окружность, касающаяся обеих сторон угла, называется вписанной в этот угол. Из только что доказанной теоремы следует, что центры всех окружностей, вписанных в данный угол (а их бесконечно много), лежат на биссектрисе этого угла (рисунок 4).
Градусная мера дуги окружности. Центральный и вписанный углы.
Чтобы дать определение градусной мере окружности, необходимо ввести понятие центрального угла. Центральным называется угол с вершиной в центре окружности.
Рассмотрим теперь несколько концентрических окружностей (то есть имеющих общий центр). Тогда любой угол с вершиной в центре окружностей будет являться центральным для каждой из них (рисунок 5). Несмотря на то, что дуги AB, PQ и MN имеют разную длину, их объединяет именно то, что каждой из них соответствует центральный угол с одной и той же градусной мерой (таким образом, каждая из названных дуг составляет одинаковую «долю» от своей окружности). Становится понятно, что характеризовать дугу исключительно ее длиной неудобно.
|
|
|
Градусной мерой дуги окружности называется градусная мера соответствующего центрального угла, если дуга меньше полуокружности, и дополняет центральный угол до 360°, если дуга больше полуокружности. Градусная мера полуокружности равна 180°. (К примеру, на рисунке 5 
, а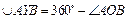 
).
Замечание 1: Градусная мера дуги окружности не превосходит 360°. Градусная мера всей окружности равна 360°.
Замечание 2: Если дуги окружности равны, то стягивающие их хорды равны. Обратно, если хорды окружности равны, то они стягивают равные дуги (на рисунке 6 дуги AB и PQ равны тогда и только тогда, когда хорды AB и PQ равны: OA = OB = OP = OQ, как радиусы. Поэтому если хорды AB и PQ равны, то ΔAOB = ΔPOQ по трем сторонам, Þ ÐAOB = ÐPOQ, то есть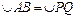 
. Если же, наоборот, 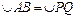, то ÐAOB = ÐPOQ, и ΔAOB = ΔPOQ по двум сторонам и углу между ними. Но тогда AB = PQ, то есть хорды окружности равны).
Ключевой в курсе планиметрии является теорема о вписанном угле. Дадим для начала определение вписанному углу: Вписанным называется угол, вершина которого лежит на окружности, а стороны пересекают окружность (на рисунке 7 угол ABC – вписанный. При этом говорят, что он опирается на дугу AC).
|
|
|
Теорема о вписанном угле: Вписанный угол равен половине градусной меры дуги, на которую он опирается.
Дано:
окружность (O; R);
A, B, C Ì (O; R).
Доказать: 
.
Доказательство:
1. 
Рассмотрим сначала случай, когда одна из сторон угла (например, BC) проходит через центр O окружности (рисунок 8а). Если провести радиус OA, то ΔAOB – равнобедренный, т.к. OA = OB = R, Þ по свойству равнобедренного треугольника, ÐOBA = ÐOAB. ÐAOC – внешний угол треугольника AOB, Þ по теореме о внешнем угле треугольника, ÐAOC = ÐOBA + ÐOAB = 2ÐOBA = 2ÐABC. Отсюда 
.
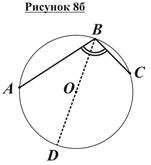
2. Рассмотрим теперь случай, когда центр окружности O лежит внутри угла ABC (рисунок 8б). Проведем диаметр BD. Тогда из пункта 1 следует, что 
.
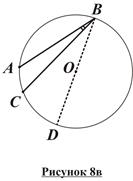
3. Если же центр O окружности лежит вне угла ABC (рисунок 8в), то аналогичным образом получаем: 
.#
Из теоремы о вписанном угле вытекают два важных следствия:
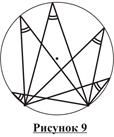
1. Вписанные углы, опирающиеся на одну и ту же дугу, равны (рисунок 9).
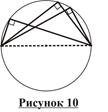
2. Угол, опирающийся на полуокружность, полуокружность (диаметр), прямой (рисунок 10).
Дата добавления: 2020-11-29; просмотров: 140; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!