Глава 2. Многочлены от n переменных
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ
КУРГАНСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
Кафедра алгебры, геометрии и методики преподавания математики
МНОГОЧЛЕНЫ
Методические указания и материалы для практических занятий по алгебре со студентами специальности 010100 - Математика
Курган 2012
Кафедра алгебры, геометрии и методики преподавания математики
Дисциплина: «Алгебра» (специальность 010100 - Математика)
Составитель: ст. преподаватель Л.М. Логиновских
Утверждены на заседании кафедры «06» декабря 2011г.
Рекомендованы методическим
советом университета «12» декабря 2011г.
содержание
Введение …………………………………………………………………..... 4
Глава 1. Многочлены от одной переменной ……………………………... 5
1. 1. Основные понятия. Алгоритм Евклида …………………….....5
1. 2. Корни многочлена. Теорема Безу. Схема Горнера ………… 11
1. 3. Приводимые и неприводимые многочлены над полем Р ….. 16
Глава 2. Многочлены от n переменных …………………………………. 29
Глава 3. Материалы для практических занятий ………………………... 40
Список литературы……………………………………………………..…. 54
введение
Настоящее пособие составлено в соответствии с программой дисциплины «Алгебра» и предназначено для студентов направления «Математика». Кроме того, пособие будет полезно студентам направления «Педагогическое образование» профиля «Математическое образование», которые также изучают данный раздел алгебры, но в несколько меньшем объеме.
|
|
|
Пособие состоит из трех разделов. В двух первых разделах содержатся основные положения теоретического курса и приведены решения типовых задач по теме «Многочлены». В последнем разделе приведено двести пятьдесят примеров и задач, которые можно использовать как для аудиторных занятий, так и для самостоятельной работы студентов.
Глава 1. Многочлены от одной переменной
1.1. Основные понятия. Алгоритм Евклида
Многочленом степени n от переменной x над полем Р называют алгебраическое выражение вида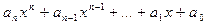 
, где n – целое неотрицательное число, 
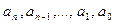– любые числа из поля Р, причем 
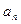¹0.
Многочлены обозначают символами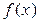 
, 
, 
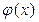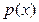и т.д.
Числа 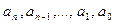называют коэффициентами многочлена, 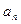– старший коэффициент, 
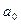– свободный член.
Одночлены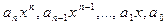 
называют членами многочлена.
Многочлен, все коэффициенты которого равны 0, называют нулевым или нуль-многочленом.
При n = 0 многочлен имеет вид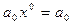 
, т.к. 
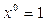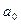, ¹ 0, т.е. многочленами нулевой степени являются числа из поля Р, отличные от 0.
Два многочлена над полем Р называют равными в алгебраическом смысле, если равны их коэффициенты при одинаковых степенях переменной x.
|
|
|
Сумма, разность и произведение двух многочленов над полем Р также являются многочленами над полем Р. Действительно, пусть
, 
.
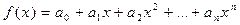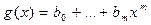Тогда
,
,
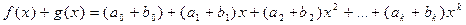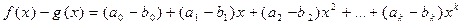где k ≤ max(n, m), причем считают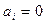 
при i > n и 
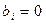при i > m.
,
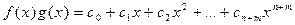где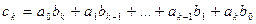 
, причем 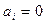при i > n и 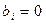при i > m.
Пусть 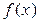и 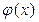¹ 0 многочлены над полем Р. Говорят, многочлен 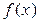делится на многочлен 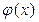, если существует такой многочлен 
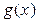над тем же полем, что выполняется равенство 
.
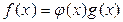Задача №1
, 
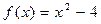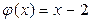, то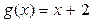 
, т.к. 
.
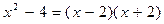Операция деления во множестве многочленов не выполнима. Выполнимо деление с остатком. Для любых двух многочленов 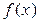и 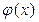¹0 над полем Р существует единственная пара многочленов 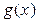и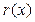 
над этим полем, которые удовлетворяют двум условиям (соотношениям):
1. 
,
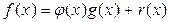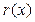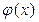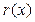2. степень меньше степени или = 0.
Задача №2
Разделить с остатком 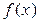на :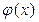
, 
.
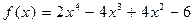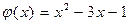Вычисления выполняются по следующей схеме:
, 
.
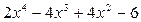
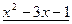
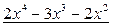
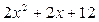
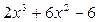
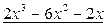
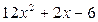
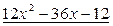
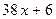
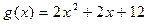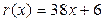Многочлен 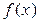делится на 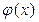в том и только том случае, если остаток при делении 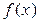на 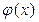равен нулю.
Задача №3
Найти a и b, при которых многочлен 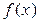делится на :
, 
.
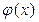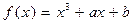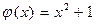Решение:
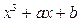
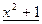
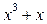
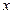
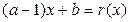
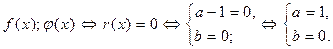
Итак, а=1, b=0.
Многочлен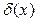 
¹ 0 называют общим делителем двух или нескольких многочленов, если каждый из них делится на .
|
|
|
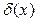Многочлен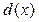 
называют наибольшим общим делителем двух или нескольких многочленов, если 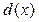является общим делителем этих многочленов и сам делится на любой другой их общий делитель.
Наибольший общий делитель двух многочленов находится однозначно с точностью до постоянного множителя, поэтому условились в качестве наибольшего общего делителя многочленов брать тот, у которого старший коэффициент равен 1.
Наибольший общий делитель двух многочленов 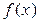и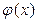 
может быть найден при помощи алгоритма Евклида, который состоит в следующем: сначала делят с остатком многочлен 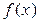на 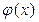, затем 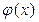на остаток от первого деления, затем остаток от первого деления на остаток от второго деления и так далее до тех пор, пока не получится нулевой остаток. Последний ненулевой остаток и есть наибольший общий делитель многочленов 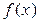и 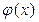. Так как постоянные множители не влияют на делимость многочленов, то в процессе применения алгоритма Евклида, чтобы исключить дробные коэффициенты, можно делимые и делители умножить на любое, отличное от нуля, число.
Задача №4
С помощью алгоритма Евклида найти наибольший общий делитель многочленов:
,
.
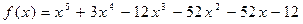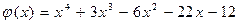Решение:
Разделим с остатком многочлен 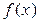на многочлен 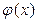. Процесс деления будем осуществлять «углом».
|
|
|
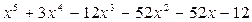
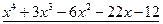
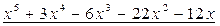
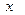
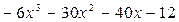
Итак,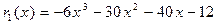 
.
Делим 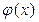на 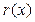. Чтобы избежать дробных коэффициентов, умножим 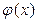на 3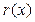, а на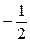 
.
; 
.
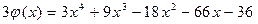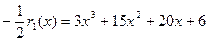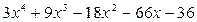
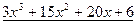
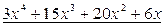
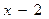
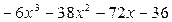
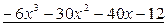
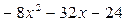
Имеем: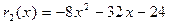 
.
Делим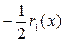 
на 
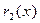, умножив предварительно на 
.
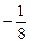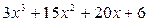
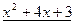
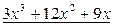
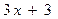
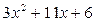
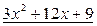
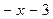
Получили, что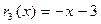 
. Умножив 
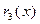на – 1, делим 
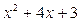на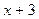 
.
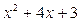
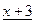
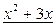
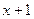
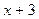
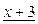
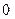
Таким образом, четвертый остаток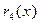 
равен нулю. Значит, наибольший общий делитель многочленов 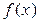и 
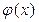равен .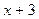
Ответ: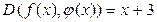 
.
Процесс решения можно оформить следующим образом:
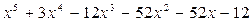
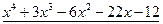
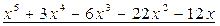
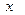
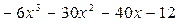
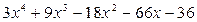
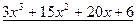
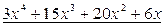
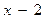
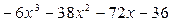
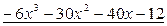
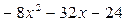
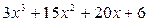
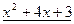
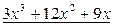
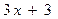
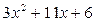
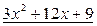
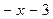
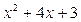
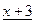
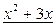
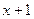
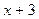
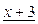
Ответ: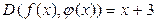 
.
Задача №5
Пользуясь алгоритмом Евклида, подобрать полиномы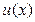 
и 
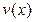так, чтобы 
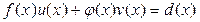, где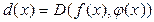 
.
,
.
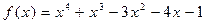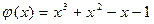При решении данной задачи используют алгоритм Евклида, но произвол, состоящий в умножении многочленов на постоянные множители, допускать нельзя, так как здесь используются и частные, которые при указанном произволе искажаются.
Найдем сначала наибольший общий делитель многочленов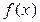 
и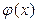 
:
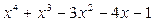
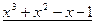
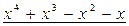
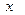
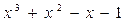
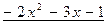
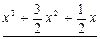
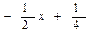
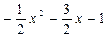
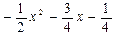
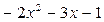
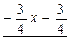
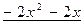
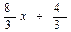
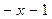
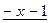
0
Итак,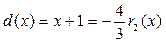 
.
Чтобы выразить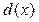 
через многочлены 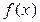и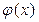 
, выразим сначала через них 
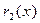. Для этого найдем 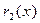из второго деления в алгоритме Евклида: 
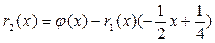. Подставив в это равенство вместо 
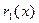его выражение, найденное из первого деления в алгоритме Евклида, получим:
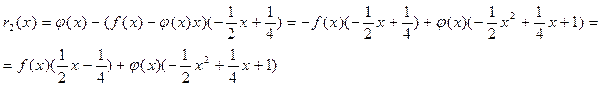
Учитывая, что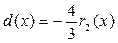 
имеем:
.
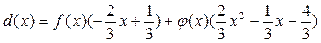Получим, что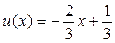 
, 
.
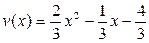1.2. Корни многочлена. Теорема Безу. Схема Горнера
Число c называют корнем многочлена 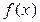, если 
.
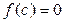Справедлива теорема Безу.
Остаток от деления многочлена 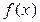на линейный двучлен 
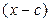равен значению многочлена при 
.
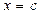Число c тогда и только тогда является корнем многочлена 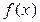, когда 
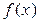делится нацело на 
.
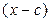Число c называют k-кратным корнем многочлена 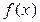, если 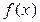делится на 
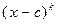, но не делится на 
.
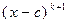Если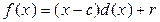 
, то коэффициенты многочлена 
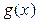и остаток r могут быть найдены по схеме Горнера:
| 
| 
| … | 
| 
| |
| 
| 
| 
| … | 
| 
|
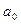
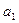
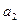
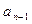
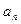
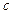
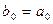
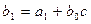
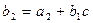
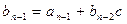
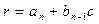
где , , …,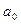 
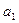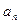– коэффициенты многочлена 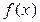, записанного по убывающим степеням x:
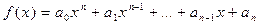, а
.
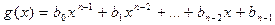Задача №6
Найти кратность корня x = 5 многочлена: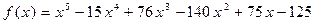 
.
Решение.
Используя схему Горнера, имеем:
| 1 | – 15 | 76 | – 140 | 75 | – 125 | |
| 5 | 1 | – 10 | 26 | – 10 | 25 | 0 |
Получим, что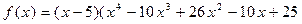 
).
Число 5 является корнем 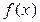. Если 5 будет корнем и 
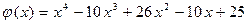, то 5 будет корнем многочлена 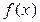второй кратности или выше.
Проверим, будет ли 5 корнем многочлена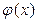 
по схеме Горнера:
| 1 | – 10 | 26 | – 10 | 25 | |
| 5 | 1 | – 5 | 1 | – 5 | 0 |
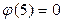, следовательно, 5 – корень .
.
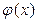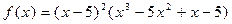Проверим, будет ли число 5 корнем многочлена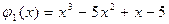 
.
| 1 | – 5 | 1 | – 5 | |
| 5 | 1 | 0 | 1 | 0 |
Число 5 является корнем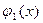 
, отсюда имеем:
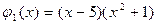, а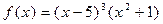 
.
Число 5 корнем многочлена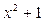 
уже не является. Следовательно, 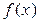делится на 
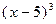, но не делится на 
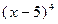. Значит, кратность корня 5 многочлена 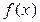равна 3.
Процесс решения можно оформить следующим образом:
| 1 | – 15 | 76 | – 140 | 75 | – 125 | |
| 5 | 1 | – 10 | 26 | – 10 | 25 | 0 |
| 5 | 1 | – 5 | 1 | – 5 | 0 | |
| 5 | 1 | 0 | 1 | 0 | ||
| 5 | 1 | 5 | 26¹0 |
Число 5 является трехкратным корнем многочлена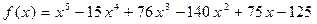 
, т.е. 
.
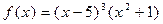Задача №7
Остатки от деления многочлена 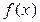на x – 2 и x – 3 равны соответственно 5 и 7. Найти остаток от деления этого многочлена на 
.
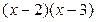Решение.
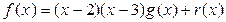
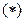, т.к. степень делителя 
равна двум, то степень остатка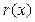 
меньше или равна единице, т.е. 
.
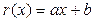По теореме Безу имеем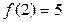 
, 
.
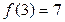При x = 2 равенство принимает вид 
,
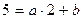При x = 3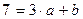 
.
Решая систему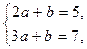 
получаем a = 2, b = 1.
Итак,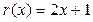 
.
Задача №8
Найти, при каких a и b многочлен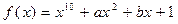 
делится на 
.
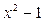Решение.
.
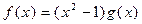При x = 1 имеем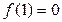 
,
При x = – 1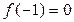 
, получаем систему
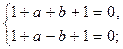
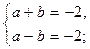отсюда a = – 2, b = 0.
Задача №9
Пользуясь схемой Горнера, разложить многочлен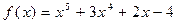 
по степеням x – 1, найти значение многочлена 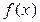и всех его производных при x = 1.
Решение.
По формуле Тейлора имеем:
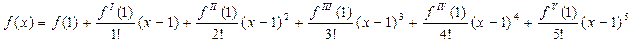- разложение многочлена 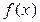по степеням x – 1.
Как видно из формулы, для решения задачи нужно найти значения многочлена 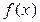и его производных при x = 1. Это можно сделать непосредственно, находя производные многочлена 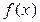, а затем их значения при x = 1.
Но для решения этой задачи можно использовать также и схему Горнера. Запишем разложение многочлена 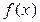по степеням (x – 1) с неопределенными коэффициентами:
.
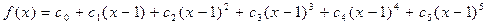Числа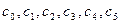 
равны соответственно остаткам от деления многочленов 
, 
, 
, 
, 
, 
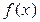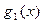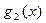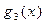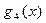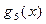на x – 1, где 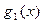есть частное от деления 
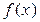на x – 1, 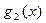есть частное от деления 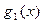на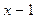 
и т.д. Наконец, 
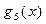есть частное от деления 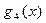на x – 1.
Все решения можно записать в схему:
| 1 | 3 | 0 | 0 | 2 | -4 | |
| 1 | 1 | 4 | 4 | 4 | 6 | 2 |
| 1 | 1 | 5 | 9 | 13 | 19 | |
| 1 | 1 | 6 | 15 | 28 | ||
| 1 | 1 | 7 | 22 | |||
| 1 | 1 | 8 | ||||
| 1 | 1 |
Отсюда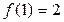 
, 
, 
, 
, 
, 
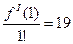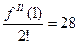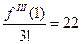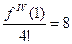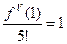, тогда , 
, 
, 
, 
, 
.
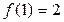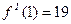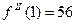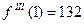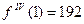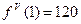Подставляем найденные значения в формулу Тейлора, имеем: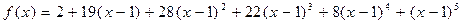 
.
Задача №10
Разложить на простейшие дроби рациональную дробь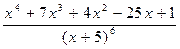 
.
Решение.
Разложим числитель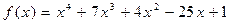 
по степеням x + 5 по формуле Тейлора, используя схему Горнера.
| 1 | 7 | 4 | – 25 | 1 | |
| – 5 | 1 | 2 | – 6 | 5 | – 24 |
| – 5 | 1 | – 3 | 9 | – 40 | |
| – 5 | 1 | – 8 | 49 | ||
| – 5 | 1 | – 13 | |||
| – 5 | 1 |
.
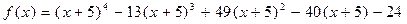Тогда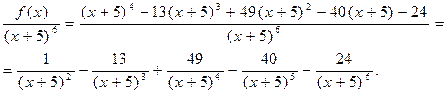 
Задача №11
Вычислить значение многочлена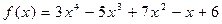 
при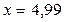 
.
Решение.
Ближайшим целым числом к 4,99 является 5, поэтому сначала разложим многочлен 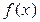по степеням x – 5 по формуле Тейлора, используя схему Горнера, а затем подставим значение x = 4,99.
| 3 | – 5 | 7 | – 1 | 6 | |
| 5 | 3 | 10 | 57 | 284 | 1426 |
| 5 | 3 | 25 | 182 | 1194 | |
| 5 | 3 | 40 | 382 | ||
| 5 | 3 | 55 | |||
| 5 | 3 |
;
;
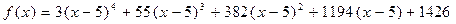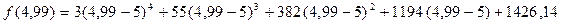
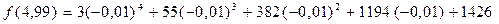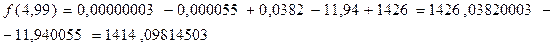
Итак,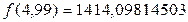 
.
1.3. Приводимые и неприводимые многочлены над полем Р
Многочлен 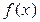степени n ³ 1 называют приводимым над полем Р, если он разлагается над этим полем на произведение двух многочленов меньшей степени и неприводимым над полем Р в противном случае.
Один и тот же многочлен может быть приводим над одним полем и неприводимым над другим, например,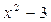 
над полем действительных чисел приводим, т.к. 
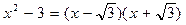, а над полем рациональных чисел он неприводим.
Многочлены первой степени неприводимы над любым полем.
Всякий многочлен 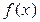над полем Р степени n ³ 1 разлагается на произведение неприводимых над этим полем многочленов, причем единственным образом с точностью до порядка следования сомножителей и множителей нулевой степени.
Всякий многочлен степени n ³ 1 над полем комплексных чисел имеет хотя бы один корень, в общем случае комплексный.
По теореме Безу многочлен, имеющий корень c, делится на x – c, поэтому всякий многочлен степени n ³ 2 приводим над полем комплексных чисел.
Над полем C неприводимы лишь многочлены первой степени, поэтому всякий многочлен n-ой степени разлагается над полем C на n линейных множителей.
Если многочлен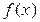 
с действительными коэффициентами имеет комплексный корень a + bi, то он имеет также корень a – bi, т.е. комплексные корни многочлена с действительными коэффициентами попарно сопряжены.
Над полем R неприводимыми многочленами являются все многочлены первой степени и часть многочленов второй степени, а именно те, у которых дискриминант меньше нуля.
Над полем рациональных чисел Q существует неприводимые многочлены любой натуральной степени, что следует из критерия Эйзенштейна.
Пусть дан многочлен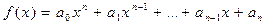 
с целыми коэффициентами. Если хотя бы одним способом можно подобрать простое число p, удовлетворяющее следующим требованиям:
1) старший коэффициент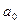 
не делится на p;
2) все остальные коэффициенты делятся на p;
3) свободный член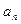 
, делясь на p, не делится на p2,
то многочлен 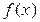неприводим над полем рациональных чисел.
Например,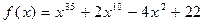 
неприводим над полем рациональных чисел, т.к. существует p = 2, удовлетворяющее условиям критерия.
Задача №12
Разложить многочлен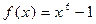 
на неприводимые множители над полем рациональных, действительных и комплексных чисел.
Решение.
1-й способ: Найдем сначала разложение над полем С.
.
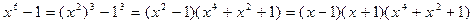Чтобы разложить многочлен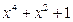 
на неприводимые множители над С, найдем его корни. Обозначим 
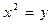, тогда 
.
;
, 
,
, 
.
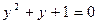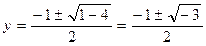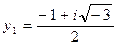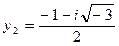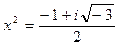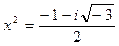Чтобы извлечь квадратный корень из числа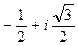 
, представим его в тригонометрической форме: 
.
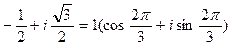Тогда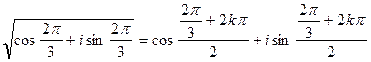 
.
При k = 0 получим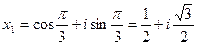 
.
При k = 1 получим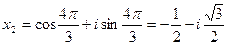 
.
Аналогично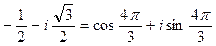 
;
.
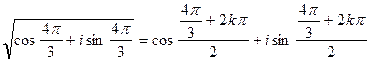При k = 0 получим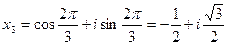 
.
При k = 1 получим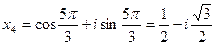 
.
Получим, что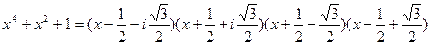 
.
Тогда разложение многочлена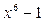 
над полем С имеет вид:
.
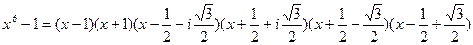Найдем разложение данного многочлена над полем действительных чисел R. Для этого в полученном разложении перемножим множители, соответствующие сопряженным корням. Перемножим третий и шестой множители: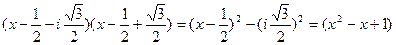 
.
Аналогично перемножим четвертый и пятый множители:
.
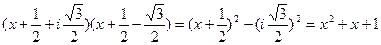Отсюда имеем разложение многочлена 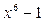на неприводимые множители над полем R: 
.
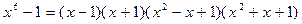Это же разложение имеет многочлен 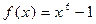и над полем рациональных чисел.
2-й способ:
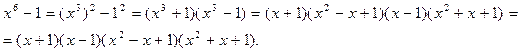
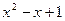над полем R неприводим, т.к. D = 1 – 4 = – 3, D < 0. Значит, 
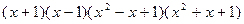– разложение многочлена 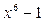на неприводимые множители над полями R и Q. Найдем разложение над полем комплексных чисел.
,
,
; 
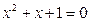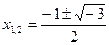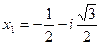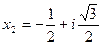, тогда 
.
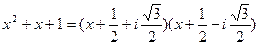Аналогично,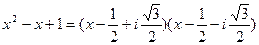 
.
Итак,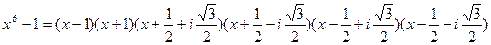 
.
Задача №13
Разложить многочлен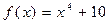 
на неприводимые множители над полями C, R, Q.
Решение.
1-й способ: Чтобы найти разложение многочлена над полем C, найдем его корни. Для этого извлечем корень четвертой степени из – 10.
.
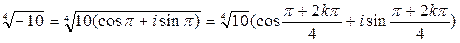Придавая k значения 0, 1, 2, 3, получим четыре корня:
, 
,
, 
.
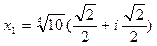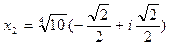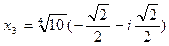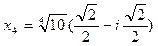Теперь можно записать разложение многочлена 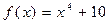над полем C:
.
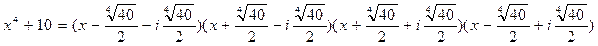Перемножая первый и четвертый множители, а затем второй и третий, получим разложение многочлена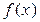 
над полем R:
.
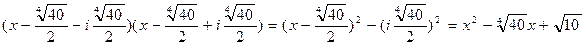
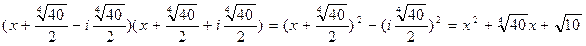
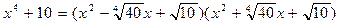Над полем рациональных чисел Q данный многочлен неприводим, так как существует p = 2 (или 5), на которое первый коэффициент 1 не делится, все остальные коэффициенты делятся, а свободный член 10, делясь на 2, не делится на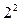 
(критерий Эйзенштейна).
2-й способ:
, 
, 
,
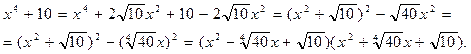
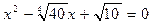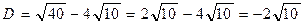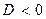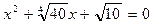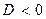, , поэтому эти многочлены неприводимы над R.
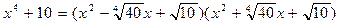– разложение многочлена над R.
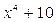над Q неприводим по критерию Эйзенштейна.
Найдем разложение над полем C:
, 
.
.
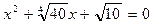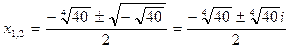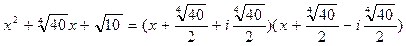Аналогично, найдем разложение:
.
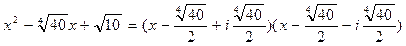Итак,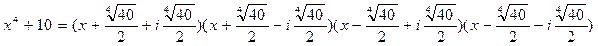 
- разложение над полем C.
Задача №14
Выяснить, какие из многочленов неприводимы над полем Q.
;
;
;
;
.
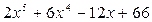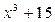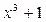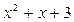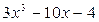Решение.
Многочлены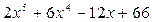 
, 
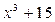неприводимы над полем Q, т.к. существует простое число p = 3, удовлетворяющее условиям критерия Эйзенштейна.
Многочлены ,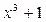 
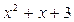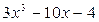, не удовлетворяют условиям критерия Эйзенштейна.
Вопрос о приводимости и неприводимости над Q решается в каждом случае индивидуально.
Многочлен 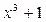приводим над Q, т.к. 
.
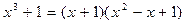Многочлен 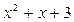неприводим на R, т.к. 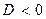, а, значит, 
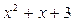неприводим и над Q.
Многочлен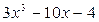 
приводим над полем Q, т.к. имеет рациональный корень 
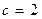, а, значит, делится на 
.
.
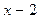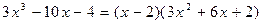Задача №15
Привести примеры многочленов степени n, неприводимых над Q.
1) n = 4; 2) n = 10; 3) n = 135; 4) n = 1000.
Решение.
Воспользуемся критерием Эйзенштейна. Возьмем любое просто число p. Пусть p = 3,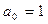 
, 
, 
, 
, 
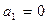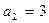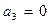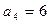, тогда многочлен 
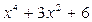искомый для n = 4.
Пусть p = 2,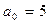 
, 
, 
, 
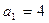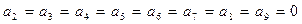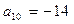, тогда многочлен 
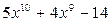– искомый для n = 10.
Аналогично находим многочлены для n = 135 и n = 1000.
Например,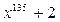 
, 
.
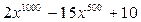Задача №16
Зная, что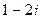 
является корнем многочлена 
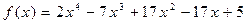, найти остальные его корни.
Решение.
Т.к. 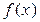есть многочлен с действительными коэффициентами, то наряду с корнем 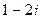он имеет корень 
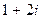. Следовательно, многочлен 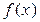делится на 
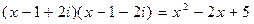. Разделив 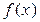на 
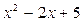, получим 
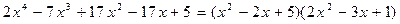. Отсюда видно, что два других корня многочлена 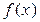есть корни уравнения 
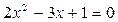, т.е. равны числам 1 и 
.
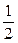Задача №17
Построить многочлены наименьшей степени над полями C и R со старшим коэффициентом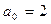 
, имеющие следующие корни: – 1 двукратный, 3 – i простой корень.
Решение.
1-й способ: Если c – корень 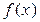, то 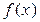делится на 
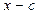. Следовательно, искомый многочлен должен делиться 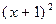на 
и на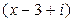 
, а так как он должен иметь наименьшую степень и 
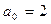, то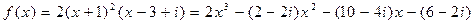 
.
2-й способ: Для решения задачи можно воспользоваться формулами Виета, которые выражают связь между корнями и коэффициентами многочлена.
Пусть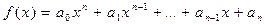 
, причем 
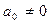и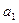 
, 
, …, 
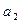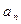– корни многочлена, каждый из которых повторен столько раз, какова его кратность.
Тогда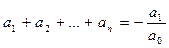 
,
,
,
…………………………………………….
.
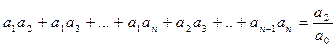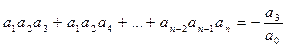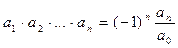Подставив вместо ,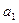 
, 
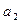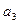соответственно числа – 1, – 1, 3 – i, и учитывая, что 
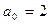, получим:
,
,
.
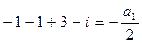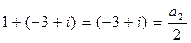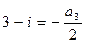Отсюда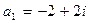 
, 
, 
.
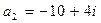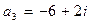
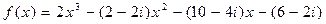Найдем многочлен над полем R.
Решение.
Так как комплексные корни многочлена c действительными коэффициентами попарно сопряжены, то наряду с корнем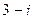 
искомый многочлен 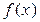должен иметь корень 
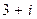. Так как нужно построить многочлен наименьшей степени с корнями – 1, – 1, 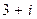, , 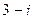то можно сделать вывод, что 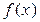имеет четвертую степень. Найдем этот многочлен двумя способами.
1-й способ:
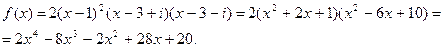
2-й способ: Воспользуемся формулой Виета:
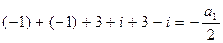, отсюда 
;
, 
;
, 
;
, 
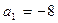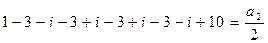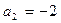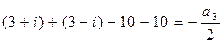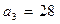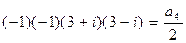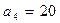
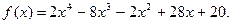
Задача №18
Найти рациональные корни многочлена
.
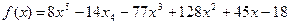Решение.
Для того чтобы найти рациональные корни многочлена, пользуются следующими теоремами.
Теорема 1. Если несократимая дробь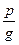 
является корнем многочлена 
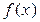с целыми коэффициентами, то p есть делитель свободного члена, а g – делитель старшего коэффициента многочлена .
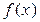Замечание: Теорема 1 дает необходимое условие для того, чтобы рациональное число 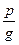было корнем многочлена. Если 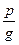такова, что p – делитель свободного члена, а g – положительный делитель старшего коэффициента, то не обязательно, что – корень .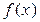
Теорема 2. Если несократимая дробь 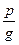является корнем многочлена 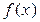с целыми коэффициентами, то при любом целом m, отличном от 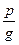, число 
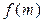делится на число p – gm, т.е. 
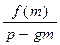– целое число.
В частности, полагая, что m = 1, а затем m = – 1, получим: если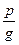 
корень многочлена, не равный ± 1, то 
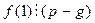и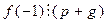 
, т.е. 
, 
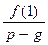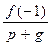– целые числа.
Замечание: Теорема 2 дает еще одно необходимое условие для рациональных корней многочлена. Это условие удобно тем, что оно легко проверяется практически. Находим сначала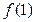 
и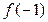 
, а затем для каждой испытываемой дроби проверяем указанное условие. Если хотя бы одно из чисел 
, 
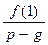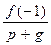дробное, то 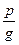корнем многочлена 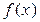не является.
Решение.
То теореме 1 корни данного многочлена следует искать среди несократимых дробей, числители которых являются делителями 18, а знаменатели – делителями 8. Следовательно, если несократимая дробь 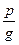есть корень 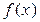, то p равно одному из чисел: ± 1, ± 2, ± 3, ±6, ±9, ±18; g равно одному из чисел: ± 1, ± 2, ±4, ± 8.
Учитывая, что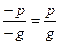 
, 
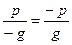, знаменатели дробей будем брать лишь положительными.
Итак, рациональными корнями данного многочлена могут быть следующие числа: ± 1, ± 2, ± 3, ±6, ±9, ±18,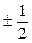 
, 
, 
, 
, 
, 
, 
, 
, 
.
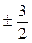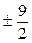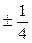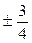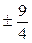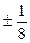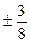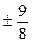Воспользуемся вторым необходимым условием.
Так как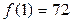 
, 
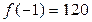, отсюда, в частности, следует, что – 1 и 1 не являются корнями 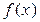. Теперь для каждой возможной дроби 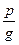будем проверять условием теоремы 2 при m = 1 и m = – 1, т.е. будем устанавливать, целыми или дробными являются числа: 
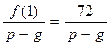и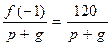 
.
Результаты сведем в таблицу, где буквы «ц» и «д» означают соответственно, целым или дробным является число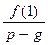 
или 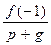(см. таблицу 1)
Таблица 1.
| p | g |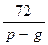 
| 
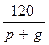
| p | g |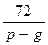 
| 
| |
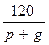
| 2 | 1 | ц | ц | 9 | 2 | д | ||
| -2 | 1 | ц | ц | -9 | 2 | д | ||
| 3 | 1 | ц | ц | 1 | 4 | ц | ц | |
| -3 | 1 | ц | ц | -1 | 4 | д | ||
| 6 | 1 | д | 3 | 4 | ц | д | ||
| -6 | 1 | д | -3 | 4 | д | |||
| 9 | 1 | ц | ц | 9 | 4 | д | ||
| -9 | 1 | д | -9 | 4 | д | |||
| 18 | 1 | д | 1 | 8 | д | |||
| -18 | 1 | д | -1 | 8 | ц | д | ||
| 1 | 2 | ц | ц | 3 | 8 | д | ||
| -1 | 2 | ц | ц | -3 | 8 | д | ||
| 3 | 2 | ц | ц | 9 | 8 | ц | д | |
| -3 | 2 | д | -9 | 8 | д |
Из полученной таблицы видно, что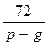 
и 
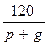являются целыми лишь в тех случаях, когда 
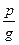равно одному из чисел: 2, – 2, 3, – 3, 9, 
, 
, 
, 
.
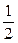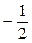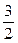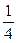По следствию из теоремы Безу число a – корень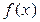 
тогда и только тогда, когда 
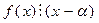. Следовательно, для проверки оставшихся девяти чисел можно применить схему Горнера деления многочлена на двучлен.
| 8 | – 14 | – 77 | 128 | 45 | – 18 | |
| 2 | 8 | 2 | – 73 | – 18 | 9 | 0 |
| 2 | 8 | 18 | – 37 | – 92 | – 172¹0 |
2 – корень.
Отсюда имеем: x = 2 – простой корень 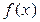. Остальные корни данного многочлена совпадают с корнями многочлена 
.
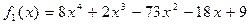Аналогично проверим остальные числа.
| 8 | 2 | – 73 | – 18 | 9 | |
| – 2 | 8 | – 14 | – 45 | 72 | – 139¹0 |
| 3 | 8 | 26 | 5 | – 3 | 0 |
| 3 | 8 | 50 | 155 | 426¹0 | |
| – 3 | 8 | 2 | – 1 | 0 | |
| – 3 | 8 | – 22 | 65¹0 | ||
| 9 | 8 | 74 | 665¹0 | ||
|
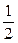
| 8 | 6 | 2¹0 | ||
|
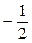
| 8 | – 2 | 0 | ||
|
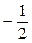
| 8 | – 6¹0 | |||
|
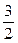
| 8 | 10¹0 | |||
|
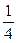
| 8 | 0 |
– 2, 9, 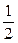, 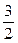– не корни; 3, –3, 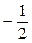, 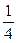- корни.
Итак, многочлен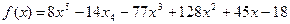 
имеет пять рациональных корней: 
.
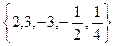Глава 2. Многочлены от n переменных
Выражение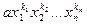 
, где а любое число из поля Р, 
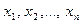– переменные, 
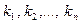– целые неотрицательные числа, называют одночленом от n переменных над полем Р.
Суммы конечного числа одночленов указанного вида называют многочленом от n переменных над полем Р.
Для обозначения многочленов от 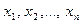пользуются символами 
, 
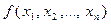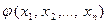и т.п.
Многочлены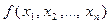 
и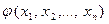 
называют равными, если для любых 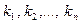коэффициент при 
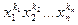многочлена 
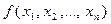равен коэффициенту при 
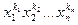многочлена 
.
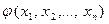Суммой двух многочленов от n переменных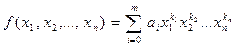 
и 
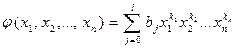называют многочлен, получающийся в результате приписывания к членам первого многочлена членов второго многочлена с теми же знаками и приведения подобных членов (членов, имеющих одинаковые наборы показателей при переменных).
Чтобы найти произведение двух многочленов, нужно все члены первого многочлена умножить на все члены второго многочлена и привести подобные члены.
Произведением одночленов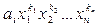 
и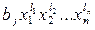 
называют одночлен вида 
.
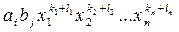Число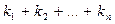 
называют степенью ненулевого одночлена 
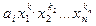. Очевидно степень произведения двух одночленов равна сумме их степеней.
Степенью (по совокупности переменных) ненулевого многочлена называют максимальную из степеней его членов.
Многочлен называют однородным степени m, если все его члены имеют степень m.
Например, многочлен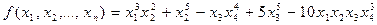 
– однородный многочлен пятой степени.
Есл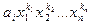и 
и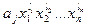 
два одночлена многочлена 
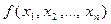, то одночлен 
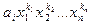считают выше одночлена 
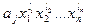, если существует натуральное число s такое, что 
.
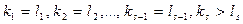Любые два одночлена сравнимы по высоте.
При записи многочлена от n переменных принято располагать его одночлены по высоте. Такое расположение членов многочлена называют лексикографическим.
Задача №19
Расположить лексикографически члены многочлена:
.
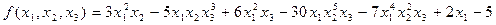Решение.
.
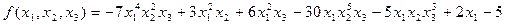Многочлен 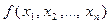называют симметричным, если он не изменится при любой перестановке входящих в него переменных .
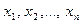При этом многочлены:
,
,
,
……………………………………..
.
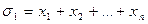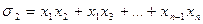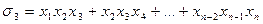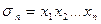называются основными симметрическими многочленами от n переменных.
Основная теорема теории симметрических многочленов заключается в том, что всякий симметрический многочлен от n переменных над полем Р может быть единственным образом представлен в виде многочлена от основных симметрических многочленов с коэффициентами из поля Р, т.е.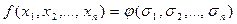 
.
Уравнение от одной переменной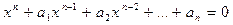 
(1) и система n уравнений от n переменных
,
,
,
……………………………………..
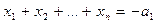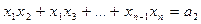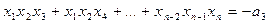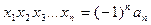. (2)
связаны между собой следующим образом. Если числа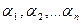 
– корни уравнения (1), то любая перестановка этих чисел является решением системы (2), т.е. система (2) имеет n решений, одним из которых будет 
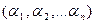и обратно, если 
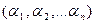одно из решений системы (2), то числа 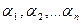являются корнями уравнения (1).
Задача №20
Выразить многочлен
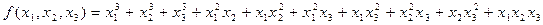
через основные симметрические многочлены.
Решение.
Данный симметрический многочлен является однородным многочленом третьей степени. Его высший член равен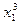 
. Ему соответствует система показателей 3 0 0 
.
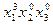Составим многочлен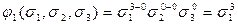 
, высший член которого совпадает с высшим членом 
.
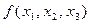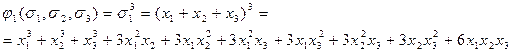
Найдем разность
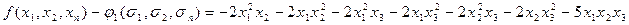
Обозначим полученный многочлен через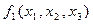 
. Высший член полученного многочлена равен 
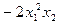. Ему соответствует система показателей 2 1 0 
.
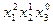Составим многочлен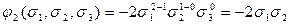 
, высший член которого совпадает с высшим членом многочлена .
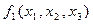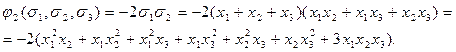
Найдем разность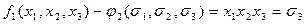 
. Отсюда следует, что 
.
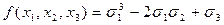В случае, когда данный многочлен является однородным, эту задачу можно решить проще.
Учитывая все возможные члены симметрических многочленов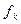 
, получающихся согласно доказательству теоремы, составим таблицу (см. таблицу 2)
Таблица 2.
| Система показателей | Высшие члены | Соответствующая комбинация основных симметрических многочленов |
| 3 0 0 |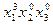
| 
|
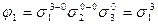
| 2 1 0 |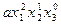 
| 
|
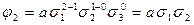
| 1 1 1 |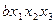 
| 
|
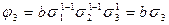
Обращаем внимание на то обстоятельство, что система показателей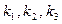 
каждого высшего члена должна удовлетворять условию 
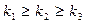, и в то же время сумма 
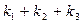должна равняться трем. Кроме того, каждая следующая система показателей должна соответствовать члену меньшей высоты.
Из приведенной таблицы получаем, что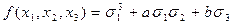 
, где a и b пока неопределенные коэффициенты. Определим их, подставляя в последнее тождество вместо 
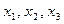некоторые числовые значения (см. таблицу 3)
Таблица 3.
| 
| 
| 
| 
| 
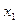
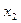
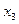
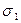
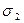
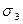
| f |
| 1 | 1 | 0 | 2 | 1 | 0 | 4 |
| 1 | 1 | 1 | 3 | 3 | 1 | 10 |
Получаем систему уравнений относительно неизвестных a и b:
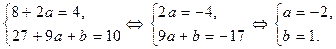
Итак,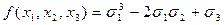 
.
Задача №21
Вычислить значение симметрического многочлена
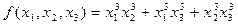, если 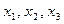– корни уравнения 
.
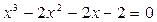Решение.
Воспользуемся следующим утверждением: если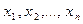 
– корни уравнения n-ой степени 
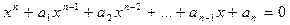, то имеют место соотношения:
x1 + x2 + … xn = – a1,
x1x2 + x1x3 + … +xn-1xn = a2,
…………………………
x1x2x3 … xn-1xn = (–1)nan.
(формулы Виета для алгебраического уравнения n-ой степени).
Следовательно, для решения данной задачи достаточно выразить многочлен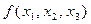 
через основные симметрические многочлены 
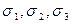. Для этого составим таблицу (таблица 4):
Таблица 4.
| Система показателей | Высшие члены | Соответствующая комбинация основных симметрических многочленов |
| 3 3 0 |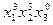 
| 
|
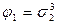
| 3 2 1 |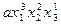 
| 
|
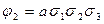
| 2 2 2 |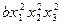 
| 
|
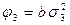
Из приведенной таблицы получается, что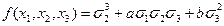 
.
Определим коэффициенты a и b (вычисления оформим в таблицу 5):
Таблица 5.
|
|
|
| 
| 
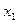
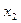
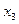
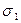
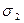
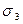
| f |
| 1 | 1 | 1 | 3 | 3 | 1 | 3 |
| 1 | 1 | – 2 | 0 | – 3 | – 2 | – 15 |
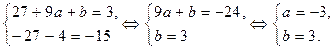
Итак,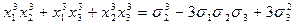 
.
Применяя формулы Виета для нашего случая, имеем:
,
,
.
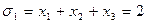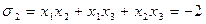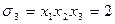Подставляя найденные значения для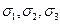 
в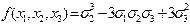 
получим: 
.
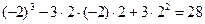Задача №22
Найти сумму кубов корней уравнения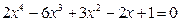 
.
Обозначим корни уравнения через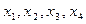 
. Нам требуется найти 
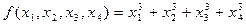, не находя самих корней 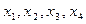. По формулам Виета найдем значения основных симметрических многочленов от корней данного уравнения. При 
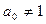формулы Виета принимают вид:
x1 + x2 + … xn = – a1,
x1x2 + x1x3 + … +xn-1xn = a2,
…………………………
x1x2x3 … xn-1xn = (–1)nan.
В нашем случае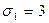 
, 
, 
, 
.
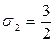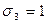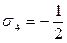Для решения задачи достаточно симметрический многочлен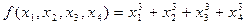 
выразить через 
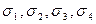. Процесс вычисления оформим в таблицу 6.
Таблица 6.
| Система показателей | Высшие члены | Соответствующая комбинация основных симметрических многочленов |
| 3 0 0 0 |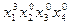 
| 
|
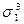
| 2 1 0 0 |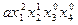 
| 
|
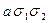
| 1 1 1 0 |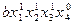 
| 
|
.
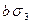
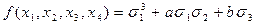Определим коэффициенты a и b (см. таблицу 7):
Таблица 7.
| 
|
| 
| 
|
| 
| 
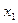
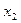
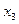
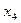
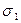
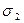
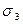
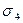
| f |
| 1 | 1 | 1 | 0 | 3 | 3 | 1 | 0 | 3 |
| 1 | 1 | 1 | 1 | 4 | 6 | 4 | 1 | 4 |
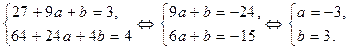
Итак,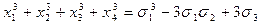 
.
Подставляя значения 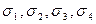получим: сумма кубов корней данного уравнения равна:
.
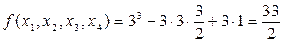Задача №23
Разложить многочлен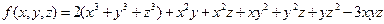 
на множители.
Решение.
Этот многочлен является однородным третьей степени с высшим членом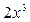 
. Представим этот многочлен через основные симметрические многочлены (см. таблицу 8):
Таблица 8.
| Система показателей | Высшие члены | Соответствующая комбинация основных симметрических многочленов |
| 3 0 0 |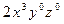 
| 
|
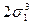
| 2 1 0 |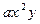 
| 
|
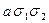
| 1 1 1 |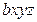 
| 
|
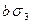
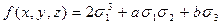
Найдем коэффициенты a и b (вычисления занесем в таблицу 9):
Таблица 9.
| x | y | z |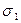
|
|
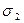
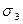
| f |
| 1 | 1 | 1 | 3 | 3 | 1 | 9 |
| 1 | 1 | 0 | 2 | 1 | 0 | 6 |
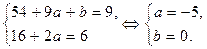
Итак,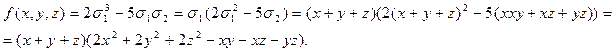 
Задача №24
Доказать, что при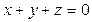 
справедливо тождество:
.
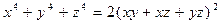Решение.
Левая и правая части равенства являются однородными симметрическими многочленами. Представим их в виде многочлена от основных симметрических многочленов (см. таблицу 10).
Таблица 10.
| Система показателей | Высшие члены | Соответствующая комбинация основных симметрических многочленов |
| 4 0 0 |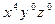 
| 
|
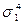
| 3 1 0 |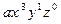 
| 
|
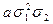
| 2 2 0 |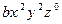 
| 
|
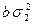
| 2 1 1 |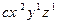 
| 
|
.
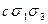
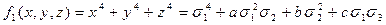Найдем a, b, c (см. таблицу 11).
Таблица 11.
| x | y | z |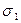
|
| 
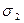
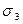
| f |
| 1 | 1 | -2 | 0 | -3 | -2 | 18 |
| 1 | 1 | 0 | 2 | 1 | 0 | 2 |
| 1 | 1 | 1 | 3 | 3 | 1 | 3 |
.
.
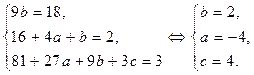
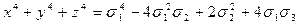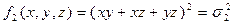Учитывая условие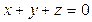 
, т.е. 
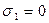, получим 
.
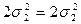Таким образом, доказываемое равенство является тождеством.
Задача №25
Решить систему уравнений:
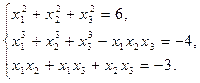
Решение.
Левые части уравнений в системе являются симметрическими многочленами от трех переменных. Выразим их через основные симметрические многочлены (таблица 12, 13).
.
.
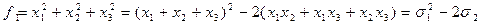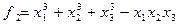Таблица 12.
| Система показателей | Высшие члены | Соответствующая комбинация основных симметрических многочленов |
| 3 0 0 |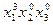 
| 
|
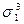
| 2 1 0 |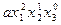 
| 
|
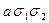
| 1 1 1 |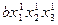 
| 
|
.
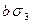
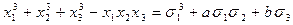Таблица 13.
| 
|
|
| 
|
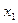
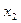
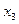
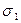
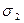
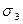
| f |
| 1 | 1 | 1 | 3 | 3 | 1 | 2 |
| 1 | 1 | 0 | 2 | 1 | 0 | 2 |
.
.
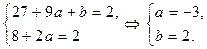
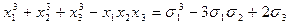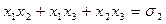Получаем систему вида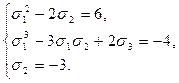 
, , 
.
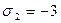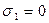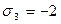Имеем систему уравнений:
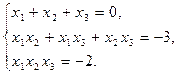
Составим уравнение третьей степени: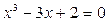 
. Найдем его корни: 
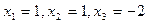. Тогда одним из решений является (1, 1, – 2), другие представляют из себя перестановки этих чисел, но так как уравнение имеет два равных корня, то система имеет только три различных решения: (1, 1, – 2), (– 2, 1, 1), (1, – 2, 1).
Дата добавления: 2020-11-27; просмотров: 549; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!