Всероссийская олимпиада школьников по математике

2015

Всероссийская олимпиада школьников по математике

Муниципальный этап

Класс

1. Натуральные числа от 1 до 127 разбили на несколько (больше одной) групп. Оказалось, что во всех группах суммы чисел равны. Доказать, что число групп чётно.

2. Рациональные числа x и y таковы, что для них справедливо равенство x³+y³=2xy. Доказать, что число 1–xy является квадратом рационального числа.

3. Укажите все точки координатной плоскости xOy, через которые график функции 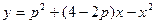не проходит ни при одном значении параметра p.

4. Четырёхугольник ABCD вписан в окружность с центром O. Точка P – точка пересечения диагоналей, точки K, L, M и N – соответственно, центры описанных окружностей треугольников AOP, BOP, COP и DOP. Доказать, что KL = MN.

5. Можно ли на плоскости можно расположить 2016 треугольников так, чтобы любые два из них имели непустое пересечение, но никакие три не имели общих точек?

Решения. 10 класс (2015)

1.Сумма S всех чисел равна S = 127×64. Число 127 – простое, а все делители числа 64, отличные от единицы – чётные. Поскольку во всех группах суммы чисел равны, общее число N групп является делителем числа S, то есть либо N=127, либо N чётно. Но равенство N = 127 означает, что в каждой группе ровно одно число, и поскольку все числа различны, такая ситуация невозможна.

2. Если x = 0, то 1 – xy = 1. Пусть x ¹ 0. Преобразуем величину 1 – xy, чтобы выделить комбинацию вида x³+y³. Для этого сначала домножим её на x²:

x²(1 – xy) = x² – x³y.

Вычитая и прибавляя y⁴, получим

x²(1 – xy) = x² – x³y – y⁴ + y⁴ = x² – y(x³ + y³) + y⁴ = x² – 2xy² + y⁴ = (x – y²)².

Из полученного равенства имеем

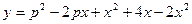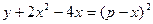3. Рассмотрим данное уравнение как уравнение относительно неизвестного p при параметрах x и y. Преобразуя его, получим и . Это уравнение имеет решения в том и только том случае, когда левая часть неотрицательна, откуда следует ответ.

Ответ:все точки, для которых y < 4x – 2x².

4. Точки K, L, M и N лежат на серединном перпендикуляре m к отрезку OP. В частности, точка K получается как точка пересечения прямой m с серединным перпендикуляром к отрезку AP, остальные три точки получаются аналогично. Покажем, что середина F отрезка OP является также и серединой отрезка KM. Для этого опустим перпендикуляры KK₁, MM₁, FG и OH на прямую AC. Точка K1 – середина отрезка AP, M1 – 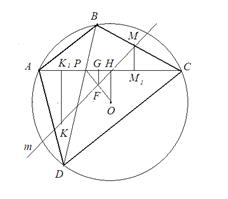середина PC, G – середина PH, а точка H – середина AC.

Получаем

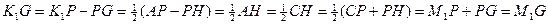По теореме Фалеса KF = FM.

Аналогично, F является и серединой отрезка LN, откуда следует требуемое утверждение.

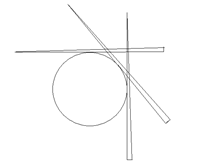5. Построим пример. Для этого рассмотрим на плоскости дугу единичной окружности w с угловой мерой p/2 и разделим её точками на 2015 равных дуг. В двух концевых точках и в 2014 точке деления проведём касательные, на которых отложим отрезки длины 4 так, что точки касания являются серединами построенных 2016 отрезков. Все построенные отрезки попарно пересекаются, при этом никакая точка пересечения двух отрезков не принадлежит никакому третьему отрезку, так как из одной точки плоскости можно провести только две касательных к данной окружности. Всего построенные отрезки имеют 2015×1008 точек попарного пересечения. Для отрезка s_i с номером i и точки пересечения M_jk отрезков с номерами j и k обозначим r_ijk расстояние от M_jk до s_i. Всего получается 2014×2015×1008 положительных чисел r_ijk, некоторые из которых равны. Среди перечисленных чисел есть наименьшее (это число – чрезвычайно мало, но оно всё-таки больше нуля). Обозначим его m. Теперь на каждом из построенных отрезков s_i как на катете построим прямоугольный треугольник D_i, второй катет которого равен m/2. Построение выполним так, чтобы прямая, содержащая больший катет, разделяла исходную единичную окружность и построенный треугольник. Все треугольники D_i, очевидно, попарно пересекаются. На рисунке представлена система из трёх таких треугольников. В полной системе треугольники ещё тоньше и примыкают друг к другу ещё плотнее.

Покажем, что никакие три из треугольников D_i не имеют общей точки. Действительно, никакая точка M_jk не содержится в треугольнике, построенном на отрезке s_i, для которого i ¹ j и i ¹ k. При этом, если прямая, содержащая катет s_i, отделяет окружность w от точки M_jk, то она отделяет от w также и пересечение треугольников, построенных на отрезках s_j и s_k. Поскольку точка M_jk удалена от s_I на расстояние, большее m, то как она сама, так и всякая точка пересечения треугольников D_j и D_k удалена от треугольника D_i на расстояние, большее m/2. Ответ: Да.

Год

Всероссийская олимпиада школьников по математике

Муниципальный этап

Класс

1. Найдите сумму целых решений уравнения = .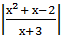

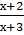2. Существуют ли целые числа х, у и z такие, что

(х –у)³ + (у –z)³ + (z – х)³ = 2018?

3. В классе учатся 32 ученика, среди них есть лодыри, способные и рыжие. Известно, что половина учеников не лодыри, способных лодырей – 5, рыжих лодырей – 3. Рыжих способных лодырей - всего 1. Сколько не рыжих и неспособных лодырей учится в классе?

4. От двух кусков сплава серебра и золота (с различным содержанием золота) массой в 6 кг и 12 кг отрезали по куску равной массы. Каждый из отрезанных кусков сплавили с остатком другого куска, после чего процентное содержание золота в обоих сплавах стало одинаковым. Какова масса каждого из отрезанных кусков?

5. Треугольник АВС равнобедренный прямоугольный с катетом 10. В него вписан равнобедренный прямоугольный треугольник PQR так, что вершины лежат на разных сторонах первого треугольника. Какова наименьшая площадь треугольника PQR?

Решения. 10 класс (2018)

1. Для области допустимых значений переменной х составим систему ограничений: 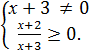Имеем х € (-∞; -3) 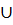[ -2; +∞).

Теперь можем избавиться от знака модуля. Следовательно, неизвестная величина х должна удовлетворять уравнению: х² + х – 2 = х + 2, которое имеет решения х₁ = -2, х₂ = 2, причем оба эти решения входят в область допустимых значений переменной х.

Ответ: 0.

2. Раскроем скобки и получим -3х² у + 3ху² – 3у²z + 3уz² – 3z ²х + 3zx². Это число делится на 3, а число 2018 на 3 не делится.

Ответ: такое равенство невозможно.

3. Так как половина учеников – лодыри, то их число равно 16. Если сложить вместе число способных и рыжих из них, получим 5 + 3 = 8. В этой сумме один способный и рыжий одновременно подсчитаны дважды, поэтому число учеников, которые являются способными и рыжими, но не одновременно, равно 8-1=7. Все остальные лодыри 16-7=9 - это одновременно и не рыжие, и неспособные.

Ответ: 9.

4. Пусть p и q – первоначальные доли золота в первом и втором кусках соответственно, х – масса отрезанного куска. Тогда доля золота в сплаве отрезанной первой части с остатком второго равна 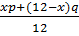, а в сплаве отрезанной части второго куска с остатком первого 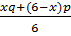. Приравнивая эти доли, получаем 3х( p - q ) =12( p - q ) (по условию p≠q), следовательно, х = 4.

Ответ: 4 кг.

5. Треугольник PQR можно вписать двумя способами.

1) Вершина прямого угла R лежит на гипотенузе АВ. Пусть М и N – проекции точки R на катеты треугольника АВС. Треугольники RMQ и RNP равны, значит, MR и NR имеют длину 5, а катет треугольника PQR не меньше 5. Тогда его площадь не менее 12,5.

2) Вершина прямого угла R лежит на катете. Пусть М – проекция вершины Q, лежащей на гипотенузе треугольника АВС, QM = MB = x, РС = у. Треугольники PCR и RMQ равны, поэтому RM = РС = у. Тогда 2х + у = 10, и гипотенуза малого треугольника имеет длину 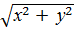. Площадь треугольника PQR равна 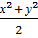= = 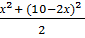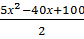. Наименьшее значение этот квадратный трехчлен достигает при х = 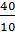= 4. Площадь такого треугольника равна 10.

Ответ 10.

Год

Дата добавления: 2020-11-27; просмотров: 117; Мы поможем в написании вашей работы!

Поделиться с друзьями:

12 3 Следующая ⇒

Мы поможем в написании ваших работ!