Оценка параметров линейной парной регрессии
Линейная парная регрессия описывается уравнением:
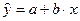, (2.6)
согласно которому изменение Δy переменной y прямо пропорционально изменению Δx переменной x (Δy = b·Δx).
Для оценки параметров a и b уравнения регрессии (2.6) воспользуемся методом наименьших квадратов (МНК). При определенных предположениях относительно ошибки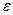 
МНК дает наилучшие оценки параметров линейной модели
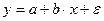. (2.7)
Согласно МНК, выбираются такие значения параметров а и b, при которых сумма квадратов отклонений фактических значений результативного признака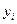 
от теоретических значений 
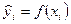(при тех же значениях фактора 
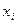) минимальна, т. е.
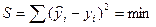(2.8)
С учетом вида линейной парной регрессии (2.6) величина S является функцией неизвестных параметров а и b
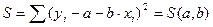. (2.9)
Следовательно, оптимальные значения параметров а и b удовлетворяют условиям
; 
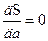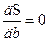. (2.10)
Выполняя соответствующие вычисления, получим для определения параметров а и b следующую систему уравнений
|
|
|
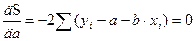
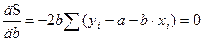
откуда после некоторых преобразований получается система нормальных уравнений метода наименьших квадратов
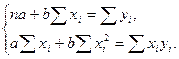(2.11)
Используя соотношения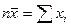 
, 
, 
, 
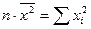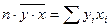из (2.8) получим
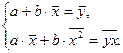(2.12)
Откуда следуют следующие выражения для определения параметров а и b
, 
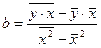. (2.13)
Формулу для параметра b можно представить следующим образом
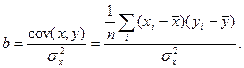(2.14)
Рассмотрим интерпретацию параметров уравнения линейной регрессии.
Коэффициент b при факторной переменной x показывает насколько изменится в среднем величина y при изменении фактора x на единицу. Например, допустим, что зависимость между затратами (тыс. руб.) и объемом выпуска продукции описывается соотношением
y = 35000+0,58·x.
В этом случае увеличение объема выпуска на 1 единицу потребует дополнительных затрат на 580 рублей.
Что касается свободного члена a в уравнении (2.6), то в случае, когда переменная x представляет собой время, он показывает уровень явления в начальный момент времени. В других случаях, параметр a может не иметь экономической интерпретации.
|
|
|
Оценка параметров нелинейных моделей
Нелинейные уравнения регрессии можно разделить на два класса:
– уравнения, которые с помощью замены переменных можно привести к линейному виду в новых переменных x', y'
(2.15)
– уравнения, для которых это невозможно. Назовем их внутренне нелинейными.
В первом случае, уравнения регрессии преобразуются к линейному виду с помощью введения новых (линеаризующих) переменных x', y'. При этом предварительно формируются массивы значений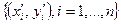 
. В последующем, после определения параметров линейного уравнения регрессии с помощью обратного преобразования можно получить параметры исходного уравнения регрессии, представляющие интерес для исследователя. Линеаризующие преобразования для некоторых нелинейных моделей приведены в таблице 2.2.
Таблица 2.2
| Зависимость | Формула | Преобразование | Зависимость между параметрами |
| Гиперболическая | 
| 
| 
|
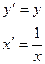
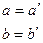
| Логарифмическая | 
| 
|
|
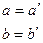
| Степенная |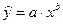 
| 
| 
|
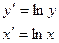
| Экспоненциальная |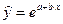 
| 
|
|
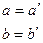
| Показательная |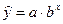 
|
| 
|
|
|
|
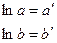
Для оценки параметров внутренне нелинейных зависимостей также можно применить метод наименьших квадратов и определять оптимальные значения параметров а и b исходя из условия (2.8) или (2.9). Но в данном случае условия (2.10) уже не являются линейными алгебраическими уравнениями относительно параметров а и b, поэтому величины параметров а и b удобнее определять непосредственно из условия (2.9) как значения, доставляющие минимум величине S.
Итерационную процедуру минимизации S в общем виде можно представить в виде следующих последовательных шагов.
1. Задаются некоторые «правдоподобные» начальные (исходные) значения 
и 
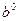
Параметров а и b.
2. Вычисляются теоретические значения 
с использованием этих значений параметров.
3. Вычисляются остатки 
и сумма квадратов остатков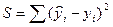 
.
4. Вносятся изменения в одну или более оценку параметров.
5. Вычисляются новые теоретические значения 
, остатки 
и S.
6. Если произошло уменьшение S, то новые значения оценок используются
в качестве новой отправной точки.
|
|
|
7. Шаги 4, 5 и 6 повторяются до тех пор, пока не будет достигнута ситуация, когда величину S невозможно будет улучшить (в пределах заданной точности).
8. Полученные на последнем шаге значения параметров а и b являются оценками параметров уравнения регрессии, полученными по нелинейным методом наименьших квадратов.
Конкретные методы минимизации S отличаются способом выбора новых измененных значений оценок параметров.
Дата добавления: 2020-11-27; просмотров: 51; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!