Величину, определяемую формулой
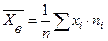, (3)
Называют выборочной средней величиной дискретного статистического распределения выборки.
Здесь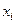 
– варианта вариационного ряда выборки; 
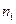– ее частота; 
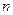– объем выборки. Если все варианты появляются в выборке лишь по одному разу, т.е. 
, то
.
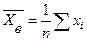2). Отклонение вариант.
Разницу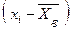 
называют отклонением вариант.
При этом
.
Следовательно, сумма отклонений всех вариант вариационного ряда выборки всегда равна нулю.
3) . Мода (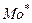 
).
Модой дискретного статистического распределения выборки называют варианта, имеющего наибольшую частоту появления.
4). Медиана (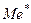 
).
Медианой дискретного статистического распределения выборки называют варианта, которая делит вариационный ряд на две части, равные по количеству вариант.
5) Дисперсия. Для измерения рассеяния вариант выборки относительно 
служит дисперсия. Дисперсия выборки – это среднее арифметическое квадратов отклонений вариант относительно , которое вычисляется по формуле:
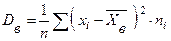(4)
або
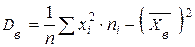. (5)
6) Среднее квадратическое отклонение.
При вычислении дисперсии отклонение возвышается к квадрату, а следовательно, меняется единица измерения признаки, поэтому на основе дисперсии вводится среднее квадратическое отклонение
|
|
|
. (6)
7) Размах вариации (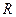 
).Для грубого оценивания рассеяния вариант относительно применяется величина, которая равна разнице между наибольшей 
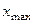и наименьшей 
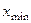вариантами вариационного ряда. Эта величина называется размахом вариации:
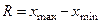. (7)
8) Коэффициент вариации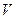 
. Для сравнения оценок вариаций статистических рядов с различными значениями , которые не равны нулю, вводится коэффициент вариации, который вычисляется по формуле
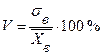. (8)
Пример. По данному статистическому распределению выборки
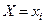
| 2,5 | 4,5 | 6,5 | 8,5 | 10,5 |
|
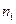
| 10 | 20 | 30 | 30 | 10 |
найти , 
, 
, , , , .
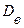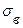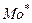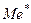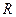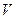Решение. Так как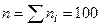 
, то, согласно формулам (3) – (8), получим:
.
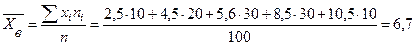Для вычисления 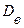найдем:
.
Тогда
.
.
.
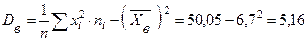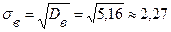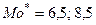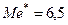, так как варианта 
делит вариационный ряд на две части, которые имеют одинаковое количество вариант.
.
.
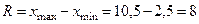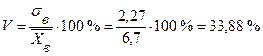Точечные оценки неизвестных параметров распределения генеральной совокупности по выборке.
|
|
|
Статистическая оценка 
, которая определяется одним числом, точкой, называется точечной. Принимая во внимание, что является случайной величиной, точечная статистическая оценка может быть смещенной и несмещенной.
Если математическое ожидание этой оценки точности равно оценочному параметру 
,
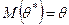то называется несмещенной, в противном случае, точечная статистическая оценка называется смещенной относительно параметра генеральной совокупности .
Оцениваемый параметр может иметь несколько точечных несмещенных статистических оценок, можно изобразить так (рис. 1):
 |
Рис. 1
Например, пусть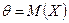 
, которая имеет две несмещенные точечные статистические оценк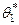и – 
и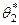 
. Тогда плотности вероятностей для 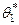і 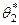имеют вид (рис. 2):
Рис. 2
Из графиков плотностей видим, что оценка 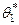по сравнению с оценкой 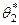имеет то преимущество, что в малой окрестности параметра , 
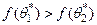. Отсюда следует, что оценка 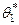чаще приобретает значение в этом окрестности, чем оценка .
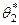Но на «хвостах» распределений имеем другую картину: большие отклонения от будут наблюдаться для статистической оценки 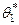чаще, чем для 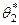. Поэтому, сравнивая дисперсии статистических оценок 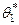, 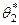как меру рассеяния, видим, что 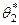имеет меньшую дисперсию, чем оценка .
|
|
|
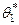Точечная статистическая оценка называется эффективной, когда при заданном объеме выборки она имеет минимальную дисперсию. Значит, оценка 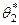будет несмещенной и эффективной.
Точечная статистическая оценка называется состоятельной, если в случае неограниченного увеличения объема выборки приближается к оценочному параметру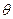 
, а именно:
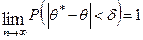
Дата добавления: 2020-11-27; просмотров: 98; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!