Среднее квадратическое отклонение.
На практике часто требуется оценить рассеяние возможных значений случайной величины вокруг ее среднего значения. Например, в артиллерии важно знать, насколько кучно лягут снаряды вблизи цели. Поэтому рассмотрим еще одну очень важную числовую характеристику случайной величины, которую называют дисперсией. Прежде чем перейти к определению дисперсии, введем понятие отклонения случайной величины от ее математического ожидания.
Отклонением называют разность между случайной величиной и ее математическим ожиданием.
Если известен закон распределения дискретной случайной величины
| 
| 
| … | 
|
| 
| 
| … | 
|
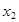
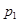
то отклонение будет иметь следующий закон распределения:
| 
| 
| … | 
|
|
|
|
| … |
|
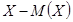
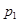
Легко доказать, что математическое ожидание отклонения равно нулю:
.
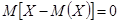По этой причине для оценки рассеяния возможных значений случайной величины отклонение не годится. В качестве меры рассеяния случайной величины берут математическое ожидание квадрата отклонения.
Дисперсией (рассеянием) дискретной случайной величины называют математическое ожидание квадрата отклонения случайной величины от ее математического ожидания:
.
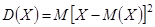По определению дисперсия равна
.
Как видим, вычисление дисперсии таким способом довольно громоздко. Укажем более удобную формулу.
Теорема. Дисперсия случайной величины равна математическому ожиданию квадрата случайной величины минус квадрат ее математического ожидания:
|
|
|
.
Доказательство. Математическое ожидание дискретной случайной величины (5.8) – это число. Для удобства обозначим его 
. Используя определение дисперсии и свойства математического ожидания (5.9), получим
,
что и требовалось доказать.
Дисперсия имеет размерность равную квадрату размерности случайной величины. В тех случаях, когда желательно, чтобы оценка рассеяния имела размерность случайной величины, вычисляют среднее квадратическое отклонение.
Определение. Средним квадратическим отклонением случайной величины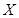 
называют положительный квадратный корень из дисперсии:
Пример 9. Случайная величина задана законом распределения
|
| -1 | 1 | 2 | 4 |
|
| 0,2 | 0,4 | 0,3 | 0,1 |
Вычислить ее дисперсию и среднее квадратическое отклонение.
Решение. Сначала вычислим математическое ожидание дискретной случайной величины (5.8):
.
Теперь найдем математическое ожидание квадрата случайной величины:
.
Искомая дисперсия равна
.
Осталось найти среднее квадратическое отклонение:
.
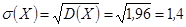Свойства дисперсии
Свойство 1. Дисперсия постоянной величины 
равна нулю:
.
Свойство очевидно, т.к. постоянная величина рассеяния не имеет.
|
|
|
Свойство 2. Постоянный множитель можно выносить за знак дисперсии, возводя его в квадрат:
.
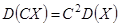Доказательство. На основании определения дисперсиидискретной случайной величины и 2 свойства математического ожидания получим
.
Свойство 3. Дисперсия суммы двух независимых случайных величин равна сумме дисперсий этих величин:
.
Доказательство. По формуле для вычисления дисперсиидискретной случайной величины (5.10) имеем
.
Раскрыв скобки и пользуясь свойствами математического ожидания (5.9 ), получим
.
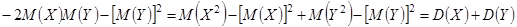Следствие. Дисперсия разности двух независимых случайных величин равна сумме их дисперсий.
.
Действительно,
.
Пример 10. В опыте с равновероятными исходами случайная величина 
приняла следующие значения: 7, 0, 2, 10, 1. Найти 
и 
.
Решение. Составим закон распределения дискретной случайной величины . Поскольку все исходы равновероятны и их всего 5, то вероятность каждого исхода (возможного значения) равна 0,2.
| 0 | 1 | 2 | 7 | 10 |
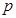
| 0,2 | 0,2 | 0,2 | 0,2 | 0,2 |
Математическое ожидание дискретной случайной величины будет равно:
.
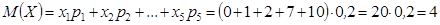Математическое ожидание квадрата случайной величины равно:
.
Вычислим дисперсию дискретной случайной величины:
|
|
|
.
Чтобы найти , воспользуемся первым и вторым свойствами дисперсии (5.11):
.
Дата добавления: 2020-11-27; просмотров: 70; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!