Алгоритм решения дифференциальных уравнений

С разделяющимися переменными

 

При решении дифференциальных уравнений с разделяющимися переменными можно руководствоваться алгоритмом:

1. разделить переменные (с учетом условий, когда это можно делать);

2. интегрируя почленно полученное уравнение с разделенными переменными, найти его общий интеграл;

3. выяснить, имеет ли уравнение решения, не получающиеся из общего интеграла;

4. найти частный интеграл (или решение), удовлетворяющий начальным условиям (если это требуется).

Закрепление.

3.1 Пример. Выполнить интегрирование методом подстановки (повторение):

 

.

 

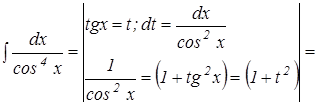
Ответ: .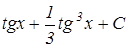

3.2 Пример № 1. Решить дифференциальное уравнение 2 xdx + 2 ydy = 0.

Решение. Уравнение представляет собой дифференциальное уравнение с разделенными переменными. Применим почленное интегрирование:

2 xdx + 2 ydy = 0

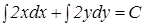                       , где С- константа

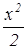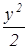2 ·  + 2 ·  = С

х² + у² = С

Следует обратить внимание, что геометрически множество решений представляет собой окружности с центром в начале координат.

Ответ: х² + у² = С

3.3 Пример № 2. Решить дифференциальное уравнение

у(1 + х) dx + x (1 + y ) dy = 0.

Решение. Уравнение       у(1 + х) dx + x (1 + y ) dy = 0                           представляет собой дифференциальное уравнение с разделяющимися переменными. Поэтому сначала преобразуем его к виду дифференциального уравнения с разделенными переменными.

Разделим обе части уравнения на  (ху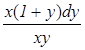) ≠ 0.

 +  = 0

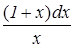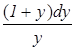 +  = 0 – получим

дифференциальное уравнение с разделенными переменными.

 Применим почленное интегрирование:

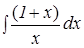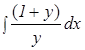 + = 0

Преобразуем подынтегральные функции для возможности удобного интегрирования с использованием таблицы интегралов:

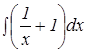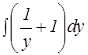 +  =С, где С- константа

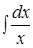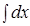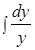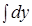 +  +  + =С ,  тогда

ln | x | + x + ln | y | + y = C .

Ответ: ln | x | + x + ln | y | + y = C .

 

3.4   Найти частное решение дифференциального уравнения х² dx + у dy = 0 , удовлетворяющее условию у (0) = 1. (Другими словами, решить задачу Коши).

Решение .

Находим общее решение дифференциального уравнения:

 

х² dx + у dy = 0

у dy = – х² dx

 

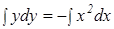
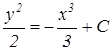 – общее решение дифференциального уравнения,

где С – константа (const)

 

Подставим начальные данные х = 0, у = 1, тогда

 

, откуда .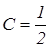

 

Значит, частное решение примет вид:

 

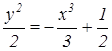,    т.е.   3у² + 2х² – 6 ·  = 0.

 

Итак,  3у² + 2х² – 3 = 0 – искомое частное решение.

Ответ: 3у² + 2х² – 3 = 0.

Задание:

1. Изучив опорный конспект, ответить на вопросы:

ü какие уравнения называются дифференциальными  уравнениями первого порядка;

ü алгоритмы решения дифференциальных уравнений первого порядка с разделенными и разделяющимися переменными;

ü постановка  и решение задачи Коши;

ü назвать виды дифференциальных уравнений первого порядка;

ü внимательно разобрать образцы решенных примеров, записать их в тетрадь;

ü выполненное (в любом удобном для вас варианте) тестовое задание выслать на электронную почту преподавателя.

2. По образцу выполнить аналогичное задание домашней контрольной работы. Задание для домашней контрольной работы необходимо взять из «Методических рекомендаций», представленных далее, по порядковому номеру в списке группы. Можно выполнить в обычной тетради, сфотографировать или решить с использованием ПК и выслать на электронную почту преподавателя.

 

---

Дата добавления: 2020-11-23; просмотров: 52; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!