Необходимое и достаточное условия существования точки перегиба.
Рассмотрим необходимое условие существования точки перегиба.
Т4. Если функция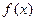 
дважды непрерывно дифференцируема на некотором интервале, содержащем точку перегиба 
, то в точке перегиба вторая производная равна нулю, т.е. 
.
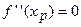PS.1. Обращение в нуль второй производной функции в точке перегиба является необходимым, но не достаточным условием существования такой точки на графике функции.
Т5. Пусть функция 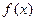дважды непрерывно дифференцируема на некотором интервале, вторая производная которой в точке 
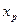, принадлежащей этому интервалу, обращается в нуль ( 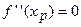) или не существует. Если при переходе через точку 
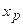вторая производная функции меняет свой знак, то точка 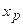определяет точку перегиба графика функции .
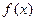Пример 8. Найти точки перегиба и интервалы выпуклости и вогнутости графика функции 
.
Найдем вторую производную заданной функции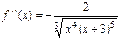 
. Найдем точки подозрительные на перегиб: а) 
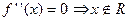б)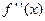 
– не существует 
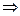знаменатель дроби обращается в ноль пр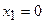и 
и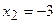 
. Отложим эти точки на числовой оси и определим знак второй производной на каждом интервале:
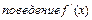–3 0
+ 
– –
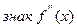Из рисунка видно, что точка 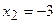является точкой перегиба, так как при переходе через нее вторая производная изменяет свой знак. Точка 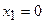не является точкой перегиба, так как при переходе через нее вторая производная не изменяет своего знака.
|
|
|
5. Асимптоты графика функции .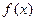
О4. Прямая (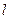 
): 
называется асимптотой графика функции 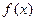, если расстояние от переменной точки графика до этой прямой стремится к нулю при стремлении аргумента 
, т.е.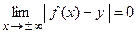 
.
PS.2. График функции может приближаться к асимптоте сверху, снизу, слева, справа или колеблясь возле этой прямой (Рис. 83).
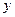
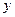
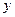
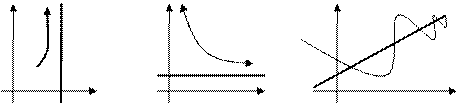
Рис. 83. Различные случаи приближения графика функции к асимптотам.
Различают вертикальные, горизонтальные и наклонные асимптоты.
О5. Вертикальная прямая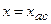 
называется вертикальной асимптотой, если 
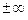. Горизонтальная прямая 
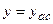называется горизонтальной асимптотой, если 
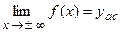. Прямая 
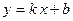называется наклонной асимптотой (параметр 
и параметр 
отличаются от 
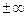и 
).
PS.3. Горизонтальная асимптота является частным случаем наклонной асимптоты: если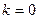 
, то наклонная асимптота вырождается в горизонтальную 
, при условии, что 
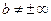. Если параметр 
, то горизонтальной асимптоты нет.
Дата добавления: 2020-11-23; просмотров: 76; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!