РЕШЕНИЕ ИГРЫ В СМЕШАННЫХ СТРАТЕГИЯХ ГЕОМЕТРИЧЕСКИМ МЕТОДОМ
Пусть игра задана платежной матрицей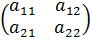 
. По оси абсцисс отложим единичный отрезок А1 А2, где точка А1 (0, 0) изображает стратегию А1, А2 (1, 0) – стратегию А2, а каждая промежуточная точка SA этого отрезка изображает смешанную стратегию первого игрока PA = (p1, p2), где p1– расстояние от точки SA до A2, p2–расстояние от точки SA до A1. Выигрыш игрока A будем откладывать на вертикальных отрезках.
Случай 1. Если игрок B применит стратегию В1, то выигрыш игрока A при стратегии А1 равен а11, поэтому на оси ординат отложим отрезок А1В1 = а11. При применении игроком A стратегии А2 выигрыш равен а21, отложим этот отрезок на перпендикуляре из точки А2, обозначим полученную точку В1'. Ордината любой точки М1 отрезка В1В1′ равна среднему выигрышу игрока A при применении смешанной стратегии SA
Случай 2. Если игрок B применяет стратегию В2, то аналогично откладываем отрезки а12 и а22 и получаем отрезок В2В2′. Ордината любой точки М2 отрезка В2В2′ – выигрыш игрока A, если A применяет смешанную стратегию SA, а B – стратегию В2.
Построим нижнюю границу выигрыша игрока А – ломаную В1 NВ2′. Ординаты точек этой ломаной показывают минимальные выигрыши игрока А при использовании им любой смешанной стратегии. Оптимальное решение игры определяет точка N, в которой выигрыш игрока А принимает наибольшее значение. Ордината точки N равна цене игры. Проекция этой точки на ось ОХ показывает оптимальную стратегию (р1, р2).
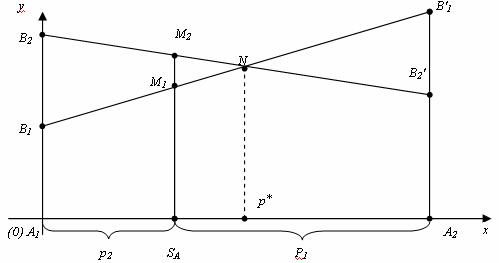
Аналогично находится оптимальная стратегия Q = (q1 , q2) игрока B, только в соответствии с принципом минимакса надо находить верхнюю границу выигрыша, т. е. строить ломаную А2NА1′ и брать точку N с наименьшей ординатой.
Абсцисса точки N определяет оптимальную стратегию игрока B, т. е. Q = (q1 , q2).
|
|
|
Пример. Решить игру, заданную платежной матрицей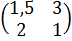 
, графоаналитическим способом.
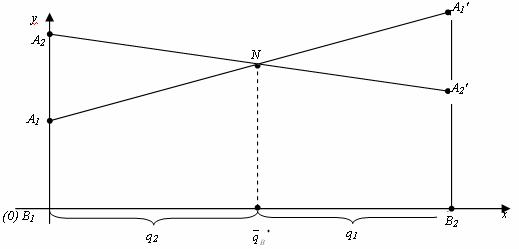
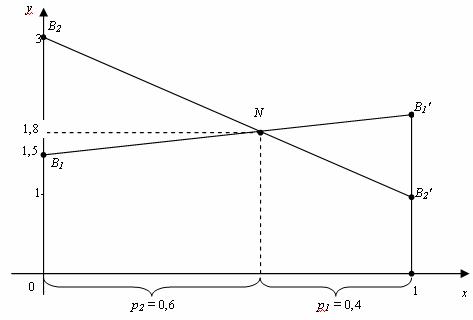
Решение. Нижняя цена игры a = 1,5, верхняя цена игры b = 2. Так как , седловой точки нет. Так как a11 = 1,5, a21 = 2 строим точки B1(0;1,5) и B2(1;2), соединяем их отрезком. Так как a12 = 3, a22 = 1 строим точки B2(0;3) и B2’(1;1), соединяем их отрезком.
Уравнение прямой В1В1′:
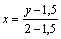, т. е. y = 0,5x + 1,5; 
, 
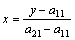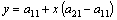
уравнение В2В2′: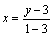 
, т. е. y = 3-2x.
Найдем точку N пересечения прямых В1В1′ и В2В2′, для чего решим систему уравнений:
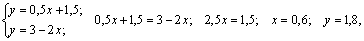
т. е. N(0,6; 1,8), откуда p2= 0,6; p1= 0,4; γ = 1,8 – цена игры.
Аналогично строим точки А1(0; 1,5) и А1′(1;3), А2(0; 2) и А2′(1; 1) и находим точку M пересечения прямых А1А1′ и А2А2′.
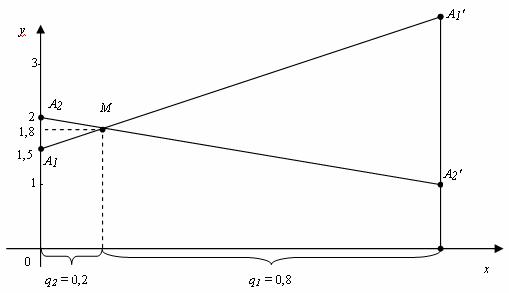
Ответ: смешанная стратегия игрока А: PA= (0,4; 0,6), игрока В: QB = (0,8; 0,2); цена игры 1,8.
Решение игр вида 2хn и mх2
Графо-аналитический метод.
У таких игр всегда имеется решение, содержащее не более двух активных стратегий для каждого из игроков. Если найти эти активные стратегии, то игра 2 х n или m х 2 сводится к игре 2 х 2, которую мы уже умеем решать. Поэтому игры 2 х n иm х 2 решают обычно графоаналитическим методом.
Рассмотрим решение матричной игры на примере.
Пример.
|
|
|
Решение.
| 1 | 4 | 7 | 1 | |
| 6 | 3 | 2 | 2 | |
| 6 | 4 | 7 | 2 4 |
a = 2, b=4, , поэтому игра не имеет седловой точки, и решение должно быть в смешанных стратегиях.
1. Строим графическое изображение игры.
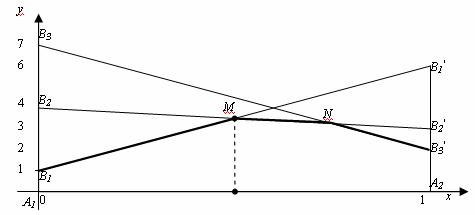
Если игрок B применяет стратегию В1, то выигрыш игрока A при применении стратегии А1 равен а11 = 1, а при использовании А2 выигрыш равен а21 = 6, поэтому откладываем отрезки А1В1 = 1, А2В1′ = 6 на перпендикулярах в А1 и А2и соединяем их отрезком. Аналогично для стратегий В2 и В3 строим отрезки В2 В2′ и В3 В3′.
2. Выделяем нижнюю границу выигрыша В1М N В3′ и находим наибольшую ординату этой нижней границы, ординату точки М, которая равна цене игрыγ.
3. Определяем пару стратегий, пересекающихся в точке оптимума М.
В этой точке пересекаются отрезки В2В2′ и В1В1′, соответствующие стратегиям В1 и В2 игрока B. Следовательно, стратегиюВ3 ему применять невыгодно. Исключаем из матрицы третий столбец и решаем игру 2 x 2 аналитически:
; 
; 
.
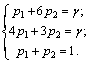
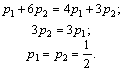
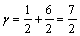
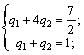
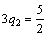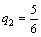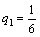Ответ: γ = 7/2; PA = (1/2; 1/2); QB = (1/6; 5/6; 0).
|
|
|
Дата добавления: 2020-11-23; просмотров: 218; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!