РЕШЕНИЯ ИГР В СМЕШАННЫХ СТРАТЕГИЯХ.

⇐ ПредыдущаяСтр 2 из 4Следующая ⇒

Если матричная игра содержит седловую точку, то ее решение находится по принципу минимакса. Если же платежная матрица не имеет седловую точку, то применение минимаксных стратегий каждым из игроков показывает, что игрок А обеспечит себе выигрыш не меньше a, а игрок В обеспечит себе проигрыш не больше b. Так как a < b, то игрок А стремится увеличить выигрыш, а игрок В уменьшить проигрыш. Если информация о действиях противной стороны будет отсутствовать, то игроки будут многократно применять чистые стратегии случайным образом с определенной вероятностью. Такая стратегия в теории игр называется смешанной стратегией.

Смешанная стратегия — стратегия, в которой чистые стратегии игроков чередуются случайным образом с некоторыми вероятностями.

Предположим, что игрок А имеет m стратегий (А₁, А₂, ..., А_m), а игрок В — n стратегий (В₁, В₂, ..., В_n). Смешанные стратегии игроков обозначим соответственно S_Аи S_В.

Смешанной стратегией S _А называется применение чистых стратегий A₁ , A₂ , … A_m с вероятностями p₁, p₂, ..., p_m , при этом .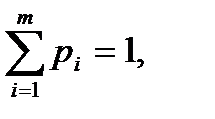

Смешанные стратегии игрока А записываются в виде матрицы

или в виде матрицы-строки S_A=(p₁, p₂,…, p_m) .

Соответственно, смешанные стратегии игрока В обозначаются

или S_В=(q₁, q₂,…, q_n), где .

Выигрыш игрока А при использовании смешанных стратегий определяется как математическое ожидание выигрыша при чистых стратегиях:

Решением игры в смешанных стратегиях называется пара оптимальных стратегий S_A^⃰ и S_В^⃰ , обладающих следующим свойством: если один из игроков придерживается своей оптимальной смешанной стратегии, то другому игроку не может быть выгодно отступать от своей.

Выигрыш, соответствующий решению, называется ценой игры.

Основная теорема теории игр Дж. фон Неймана: любая парная конечная игра с нулевой суммой имеет, по крайней мере, одно решение, возможно среди смешанных стратегий.

Следствие: каждая конечная игра имеет цену, которую обозначим через g, причем a £ g £ b.

Чистые стратегии игроков в их оптимальных смешанных стратегиях называются активными.

Теорема об активных стратегиях. Применение оптимальной смешанной стратегии обеспечивает игроку максимальный средний выигрыш (или минимальный средний проигрыш), равный цене игры g , независимо от того, какие действия предпринимает другой игрок, если только он не выходит за пределы своих активных стратегий.

Сформулированная теорема имеет огромное практическое значение, т.к. она позволяет найти оптимальные стратегии при отсутствии седловой точки.

Рассмотрим наиболее простой случай конечной игры 2 ´ 2 без седловой точки с матрицами:

С платежной матрицей

Требуется найти оптимальные смешанные стратегии игроков 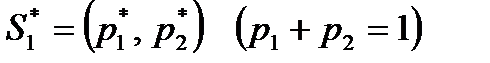, и цену игры g.

Каковы бы ни были действия противника, выигрыш будет равен цене игры g. Это означает, что если игрок I придерживается своей оптимальной стратегии 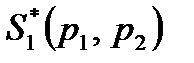, то игроку II нет смысла отступать от своей оптимальной стратегии .

В игре 2 ´ 2, не имеющей седловой точки, обе стратегии являются активными.

Для игрока I имеем систему уравнений:

Для игрока II аналогично:

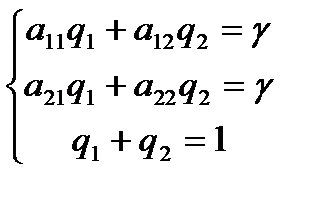
Если g ¹ 0 и игроки имеют только смешанные оптимальные стратегии, то определитель матрицы не равен нулю, следовательно, эти системы имеют единственное решение.

Решая систему уравнений (10) и (11) находим оптимальные решения 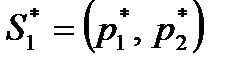, и g:

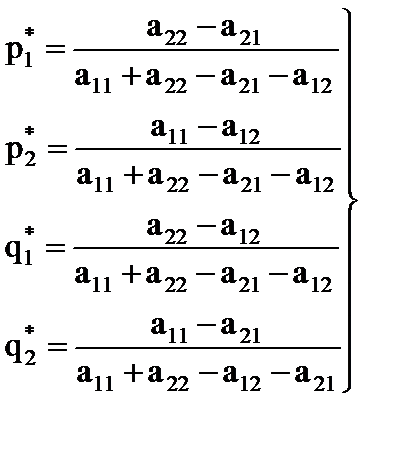q₂⃰ можно найти по формуле q₂⃰=1- q₁⃰

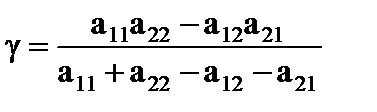
Пример: Дана платежная матрица:

Найти решение.

Решение. Так как a = 3, b = 5, то a ¹ b, то и матрица игра не имеет седловой точки. Следовательно, решение ищем в смешанных стратегиях. Запишем системы уравнений:

для игрока I:

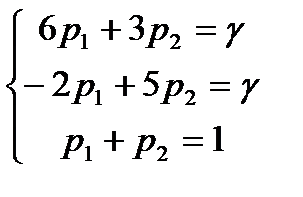
для игрока II:

Решив эти системы находим:

Следовательно, оптимальные стратегии игроков имеют вид:

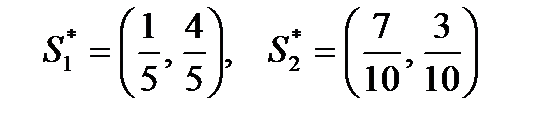Дата добавления: 2020-11-23; просмотров: 363; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 123 4 Следующая ⇒

Мы поможем в написании ваших работ!