Точечные и интервальные оценки параметров
Распределения
Пусть q - неизвестный параметр генеральной совокупности. Его приближенное значение q*, найденное по результатам случайной выборки, называется точечной оценкой генерального параметра. Величина q* случайна и зависит от значений признака 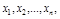 составивших выборочную совокупность:
составивших выборочную совокупность:

Выборочная оценка q* может достойно представлять неизвестный параметр q, если она обладает следующими свойствами:
1) несмещенность, когда 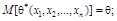
2) состоятельность , когда 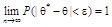 ;
;
3) несмещенная оценка считается эффективной, если 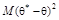 минимально.
минимально.
Известно, что выборочная средняя 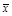 является несмещенной оценкой генеральной средней а, так как
является несмещенной оценкой генеральной средней а, так как  выборочная дисперсия
выборочная дисперсия 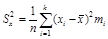 является смещенной оценкой генеральной дисперсии, так как
является смещенной оценкой генеральной дисперсии, так как  Поэтому при малых объемах выборки n пользуются “исправленной” дисперсией
Поэтому при малых объемах выборки n пользуются “исправленной” дисперсией
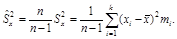 (10.9)
(10.9)
Если случайная величина Х в генеральной совокупности распределена по нормальному закону 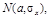 то выборочная средняя
то выборочная средняя 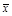 и дисперсия
и дисперсия 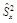 явля-ются состоятельными и эффективными оценками соответствующих генеральных параметров.
явля-ются состоятельными и эффективными оценками соответствующих генеральных параметров.
Интервальной оценкой генерального параметра q называется доверительный интервал 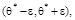 который с вероятностью a содержит параметр q, т.е.
который с вероятностью a содержит параметр q, т.е. 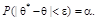 Вероятность a принято называть доверительной вероятностью. Если случайная величина Х распределена по закону
Вероятность a принято называть доверительной вероятностью. Если случайная величина Х распределена по закону 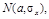 причем параметр sх неизвестен, то для интервальной оценки генеральной средней используется случайная величина
причем параметр sх неизвестен, то для интервальной оценки генеральной средней используется случайная величина
|
|
|
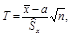
подчиненная t – распределению Стьюдента. Ее значения ta, соответствующие доверительной вероятности a и числу степеней свободы n–1, находят в таблице распределения Стьюдента (Приложения, табл. 5). Доверительный интервал для генеральной средней в этом случае имеет следующий вид:
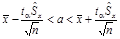 . (10.10)
. (10.10)
Для интервальной оценки генеральной дисперсии используется случайная величина
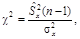
значения которой при заданной вероятности a и числе степеней свободы n–1 можно найти в табл. 4 Приложений. В этом случае доверительный интервал для генеральной дисперсии имеет вид
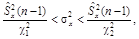 (10.11)
(10.11)
где 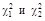 берутся из табл. 4 для вероятностей
берутся из табл. 4 для вероятностей 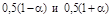 соответственно.
соответственно.
В том случае, когда объем выборки n достаточно велик, для интервального оценивания генеральной средней вид закона распределения Х уже не имеет значения, так как выборочная средняя 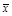 как сумма n случайных величин согласно центральной предельной теореме распределена асимптотически нормально. При этом случайная величина
как сумма n случайных величин согласно центральной предельной теореме распределена асимптотически нормально. При этом случайная величина 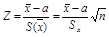 подчинена закону
подчинена закону 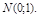
|
|
|
Тогда интервальная оценка генеральной средней выглядит так:
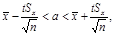 где
где  , а
, а 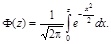 (10.12)
(10.12)
10.9. Произведено 10 независимых измерений напряжения в сети, отклонение которого от номинала распределено нормально с неизвестными параметрами.
Найти интервальные оценки для неизвестных математического ожидания и дисперсии отклонения напряжения при доверительной вероятности 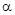 = 0,95.
= 0,95.
| Порядк. № измерения | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
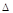 U, в U, в
| 2,5 | 2,0 | -2,3 | 1,9 | -2,1 | 2,3 | 2,4 | -2,5 | 1,5 | -1,7 |
¢ Вычислим выборочную среднюю и дисперсию случайной величины DU.
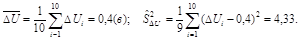
Далее из табл. 5 Приложений при  = 0,95 и n= n - 1 = 9 находим ta = 2,26.
= 0,95 и n= n - 1 = 9 находим ta = 2,26.
Вычисляем предельное отклонение e:
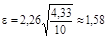 .
.
Находим доверительный интервал для генеральной средней:
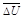 -
- 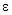 = -1,18 ;
= -1,18 ; 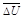 +
+ 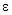 = 1,98 , значит -1,18 < DU < 1,98.
= 1,98 , значит -1,18 < DU < 1,98.
Теперь из таблицы 4 Приложений при n = n - 1 = 9 и
|
|
|
 находим:
находим:
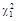 = 20,7 и
= 20,7 и 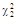 =3,275.
=3,275.
Тогда 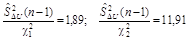 , т.е. доверительный интервал для
, т.е. доверительный интервал для 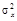 имеет границы (1,89 ; 11,91). £
имеет границы (1,89 ; 11,91). £
10.10. Результаты измерений диаметра валика ротора электродвигателя сведены в интервальный вариационный ряд:
| Х, мм | 18,70- 18,72 | 18,72- 18,74 | 18,74- 18,76 | 18,76- 18,78 | 18,78- 18,80 | 18,80- 18,82 | 18,82- 18,84 | 18,84- 18,86 | 18,86- 18,88 |
| m | 5 | 27 | 42 | 78 | 51 | 26 | 8 | 2 | 1 |
Требуется: 1) определить числовые характеристики распределения, считая их неизвестными; 2) найти интервальную оценку генеральной средней при доверительной вероятности 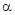 = 0,95.
= 0,95.
¢ Составим рабочую таблицу (10.4) и преобразуем интервальный ряд в дискретный, выбрав в качестве хi середины заданных интервалов; вычислим последовательно 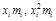 и накопленную частоту Si.
и накопленную частоту Si.
Таблица 10.4
| X | xi | mi | ximi | xi2mi | Si |
| 18,70 –18,72 | 18,71 | 5 | 93,55 | 1750,32 | 5 |
| 18,72 –18,74 | 18,73 | 27 | 505,71 | 9471,95 | 32 |
| 18,74 –18,76 | 18,75 | 42 | 787,5 | 14765,62 | 74 |
| 18,76 –18,78 | 18,77 | 78 | 1464,06 | 27480,41 | 152 |
| 18,78 –18,80 | 18,79 | 51 | 958,29 | 18006,27 | 203 |
| 18,80 –18,82 | 18,81 | 26 | 489,06 | 9199,22 | 229 |
| 18,82 –18,84 | 18,83 | 8 | 150,64 | 2836,55 | 237 |
| 18,84 –18,86 | 18,85 | 2 | 37,7 | 710,64 | 239 |
| 18,86 –18,88 | 18,87 | 1 | 18,87 | 356,08 | 240 |
| Сумма | 240 | 4505,38 | 84577,06 |
|
|
|
По результатам вычислений получаем:
- выборочную среднюю 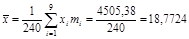 (мм);
(мм);
- выборочную дисперсию
 ;
;
- среднее квадратичное отклонение 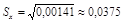 (мм).
(мм).
Для интервальной оценки генеральной средней найдем сначала значение аргумента t функции Лапласа Ф(t) при  = 0,95:
= 0,95:
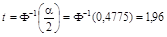 .
.
Затем, вычислив предельное отклонение
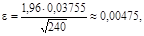
получим доверительный интервал для генеральной средней а:
18,768 < 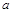 < 18,777 . £
< 18,777 . £
В задачах 10.11 – 10.13 случайные величины подчинены нор-мальному распределению. Требуется: 1) вычислить выборочную среднюю и дисперсию; 2) найти интервальные оценки для математического ожидания и дисперсии признака в генеральной совокупности при заданной доверительной вероятности a = 0,98.
10.11.
Х = {4,90; 4,51; 4,84; 4,08; 2,90; 5,67; 5,41; 6,49; 9,11; 6,89; 7,18; 6,98}.
10.12.
Х = {71,48; 67,96; 43,06; 59,20; 47,24; 68,30; 55,56; 48,86; 47,72; 50,71; 66,29; 54,65; 59,50; 76,50; 47,97; 58,23}.
10.13.
Х = {1,033; 0,987; 0,191; 0,347; 0,843; 0,671; 0,548; 0,821; 0,962; 0,864; 0,802; 0,639; 0,714; 0,658; 0,772; 1,014; 0,838; 0,908; 0,955; 0,797}.
В задачах 10.14 – 10.19 найти интервальные оценки для генеральной средней заданной случайной величины при доверительной вероятности a = 0,95.
10.14. Распределение скорости автомобилей на одном из участков шоссе (км/час):
| Границы интервалов | 61-65 | 65-69 | 69-73 | 73-77 | 77-81 | 81-85 | 85-89 | 89-93 | 93-97 | 97-101 |
| Частоты | 1 | 4 | 5 | 8 | 14 | 9 | 6 | 1 | 1 | 1 |
10.15. Суммарное число набранных баллов в соревнованиях:
| Границы интервалов | 49 – 52 | 52 – 55 | 55 – 58 | 8 – 61 | 61 – 64 | 64 – 67 | 67 –70 |
| Частоты | 3 | 6 | 11 | 19 | 30 | 21 | 10 |
10.16. Распределение предела прочности образцов сварного шва (H/мм2):
| Границы интервалов | 28 – 30 | 30 – 32 | 32 – 34 | 34 – 36 | 36 – 38 | 38 – 40 | 40 – 42 | 42 – 44 |
| Частоты | 8 | 15 | 15 | 12 | 15 | 20 | 10 | 5 |
10.17. Распределение отклонений напряжения от номинала (мВ):
| Границы интервалов | 0,00-0,02 | 0,02-0,04 | 0,04-0,06 | 0,06-0,08 | 0,08-0,10 | 0,10-0,12 | 0,12-0,14 | 0,14-0,16 |
| Частоты | 9 | 15 | 29 | 35 | 32 | 19 | 8 | 3 |
10.18. Время выполнения упражнения (с):
| Границы интервалов | 8,95-9,05 | 9,05-9,15 | 9,15-9,25 | 9,25-9,35 | 9,35-9,45 | 9,45-9,55 | 9,55- 9,65 |
| Частоты | 4 | 8 | 11 | 7 | 5 | 3 | 2 |
10.19. Горизонтальное отклонение от цели (м) для 200 испытаний ракет:
| Границы интервалов | - 40 – -30 | -30 – -20 | -20 – -10 | -10 – 0 | 0 – 10 | 10 – 20 | 20 – 30 | 30 – 40 | 40 – 50 | 50 – 60 |
| Частоты | 7 | 11 | 15 | 29 | 49 | 41 | 26 | 17 | 7 | 3 |
10.20. Результаты 16 измерений емкости конденсатора показали, что выборочная средняя равна 20 мкФ, среднее квадратическое отклонение – 4 мкФ. Считая распределение нормальным, найти 90%- и 99%-ные интервальные оценки для математического ожидания емкости конденсатора.
10.21. Имеются точечные оценки случайной величины Х – времени безотказной работы термодатчика газоанализатора, полученные по результатам 100 измерений: 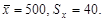 Найти доверительный интервал для генеральной средней этой случайной величины при заданной вероятности a = 0,98.
Найти доверительный интервал для генеральной средней этой случайной величины при заданной вероятности a = 0,98.
10.22. Найти 95%-ную интервальную оценку математического ожидания нормальной случайной величины Х по результатам выборки объема n = 25, если выборочная средняя равна 14, а выборочная дисперсия равна 25.
10.23. Найти минимальный объем выборки, при котором с надежностью 0,975 отклонение выборочной средней от генеральной не превысит e = 0,3, если известно среднее квадратическое отклонение s = 1,2 нормально распределенной случайной величины.
Дата добавления: 2020-11-23; просмотров: 171; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
