Числовые характеристики выборочной
МАТЕМАТИЧЕСКАЯ СТАТИСТИКА
ОСНОВЫ ВЫБОРОЧНОГО МЕТОДА
Первичная обработка результатов наблюдений
Математическая статистика оперирует количественными признаками случайных массовых явлений, которые проявляются в виде значений некоторой случайной величины (случайного признака).
Разработка методов регистрации, описания и анализа экспериментального материала составляет предмет математической статистики.
Основными задачами математической статистики являются определение неизвестного закона распределения наблюдаемой случайной величины или систем, статистическая проверка гипотез о параметрах и законах распределения, нахождение оценок параметров распределения.
Конечное или бесконечное множество всех возможных значений случайного признака называется генеральной совокупностью.
Выборочной совокупностью, или просто выборкой объема n из генеральной совокупности называется последовательность n значений случайной величины Х, полученных в n независимых повторениях эксперимента. Выборка может быть представлена в виде простого перечня значений случайного признака (при малом объеме n) 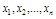 или в виде вариационного ряда – таблицы значений признака
или в виде вариационного ряда – таблицы значений признака  и им соответствующих частот
и им соответствующих частот 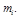
Схема составления вариационного ряда такова:
1) среди всех 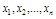 найти хнаим и хнаиб , вычислить размах вариации R = = xнаиб - хнаим ;
найти хнаим и хнаиб , вычислить размах вариации R = = xнаиб - хнаим ;
2) выбрать количество разрядов k, руководствуясь условием 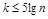 (обычно k = 8 ¸ 12) и вычислить шаг ряда
(обычно k = 8 ¸ 12) и вычислить шаг ряда 
|
|
|
3) разбить промежуток (хнаим , хнаиб ) на k интервалов точками 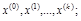 при этом границы разбиения должны быть удобными для дальнейших вычислений;
при этом границы разбиения должны быть удобными для дальнейших вычислений;
4) подсчитать количество значений признака, оказавшихся в интервалах 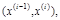 т.е. определить частоту mi попадания случайного признака Х в i – й интервал (или относительную частоту
т.е. определить частоту mi попадания случайного признака Х в i – й интервал (или относительную частоту 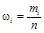 );
);
5) составить таблицу, в которой каждому интервалу 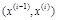 соответствует частота mi , показывающая, сколько значений случайного признака из выборочной совокупности оказалось в этом интервале; при этом следует заранее решить, какая из границ, левая или правая, принадлежит данному интервалу (табл. 10.1).
соответствует частота mi , показывающая, сколько значений случайного признака из выборочной совокупности оказалось в этом интервале; при этом следует заранее решить, какая из границ, левая или правая, принадлежит данному интервалу (табл. 10.1).
Таблица 10.1
| Интервалы значений признака Х | x (0) – x (1) | x (1) – x (2) | . . . | x (k-1) – x (k) |
| Дискретные значе-ния признака xi | x 1 | x 2 | . . . | x k |
| Частоты признака mi | m 1 | m 2 | . . . | mk |
| Относительные частоты wi | w 1 | w 2 | . . . | w k |
Интервальный ряд может быть преобразован в дискретный вариационный ряд. Для этого в каждом интервале 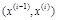 надо выбрать какое-либо значение xi (обычно это середина интервала).
надо выбрать какое-либо значение xi (обычно это середина интервала).
|
|
|
Накопленной частотой Si признака xi (или соответствующего интервала) называется сумма всех предыдущих частот, включая частоту i-го признака:
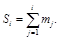
Аналогично: накопленная относительная частота 
Очевидно, что 
|
|
Накопленная относительная частота является статистической функцией распределения случайного признака и обозначается 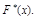
|
|
|
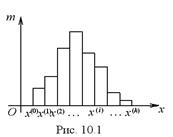
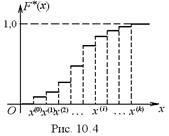
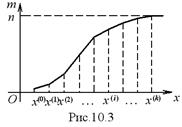
Графической иллюстрацией интервального вариационного ряда является гистограмма (рис. 10.1), дискретного вариационного ряда – полигон (многоугольник) частот (рис. 10.2); графическая иллюстрация накопленной частоты называется кумулятивной кривой (рис. 10.3), график статистической функции распределения показан на рис. 10.4.
|
|
 |
Полигон частот по форме аналогичен графику плотности распределения случайной величины в выборочной совокупности.
10.1. По данным 55 наблюдений составить интервальный вариационный ряд, преобразовать его в дискретный ряд, вычислить накопленные частоты и составить статистическую функцию распределения.
|
|
|
17 19 23 18 21 15 16 13 20 18 15 20 14 20 16 14 20 19 15 19 16 19 15 22 21 12 10 21 18 14 14 17 16 13 19 18 20 14 16 20 19 17 18 18 21 17 19 17 13 17 11 18 19 19 17
¢ Размах вариации R = 24 – 10 = 14; из неравенства k £ 5 lg55 = = 8,7 определяем, что число разрядов можно принять равным 7. Тогда длина интервала  Условимся считать, что каждому интервалу, кроме последнего, принадлежит только левая граница. Результаты группировки и вычислений записаны в таблице (10.2). £
Условимся считать, что каждому интервалу, кроме последнего, принадлежит только левая граница. Результаты группировки и вычислений записаны в таблице (10.2). £
Таблица 10.2
| Границы интерва-лов | Середина интерв. х i | Частота признака mi | Накопл. частота Si | Относит. частота w i | Статистич. функц. распр. F *(x) |
| 10 – 12 | 11 | 2 | 2 | 0,0364 | 0,0364 |
| 12 – 14 | 13 | 4 | 6 | 0,0727 | 0,1091 |
| 14 – 16 | 15 | 8 | 14 | 0,1455 | 0,2546 |
| 16 – 18 | 17 | 12 | 26 | 0,2182 | 0,4728 |
| 18 – 20 | 19 | 16 | 42 | 0,2909 | 0,7637 |
| 20 – 22 | 21 | 10 | 52 | 0,1818 | 0,9455 |
| 22 – 24 | 23 | 3 | 55 | 0,0545 | 1,0000 |
В задачах 10.2 – 10.4 требуется: 1) составить вариационный ряд; 2) вычислить накопленные частоты и статистическую функцию распределения; 3) построить гистограмму, полигон частот, кумулятивную кривую и график статистической функции распределения.
10.2. Контроль степени износа (в процентах) одинаковых элементов некоторого автоматического устройства за период времени Т дал следующие результаты:
|
|
|
13,4 14,7 15,2 15,1 13,0 8,8 14,0 17,9 15,1 16,5 16,6 14,2 16,3 14,6 11,7 16,4 15,1 17,6 14,1 18,8 11,6 13,9 18,0 12,4 17,2 14,5 16,3 13,7 15,5 16,2 8,4 14,7 15,4 11,3 10,7 16,9 15,8 16,1 12,3 14,0 17,7 14,7 16,2 17,1 10,1 15,8 18,3 17,5 12,7 20,7 13,5 14,0 15,7 21,9 14,3 17,7 15,4 10,9 18,2 17,3 15,2 16,7 17,3 12,1 19,2
10.3. Измерения емкости у 80 полевых транзисторов дали следующие результаты:
1,9 3,1 1,3 0,7 3,2 1,1 2,9 2,7 2,7 4,0 1,7 3,2 0,9 0,8 3,1 1,2 2,6 1,9 2,3 3,2 4,1 1,3 2,4 4,5 2,5 0,9 1,4 1,6 2,2 3,1 1,5 1,1 2,3 4,3 2,1 0,7 1,2 1,5 1,8 2,9 0,8 0,9 1,7 4,1 4,3 2,6 0,9 0,8 1,2 2,1 3,2 2,9 1,1 3,2 4,5 2,1 3,1 5,1 1,1 1,9 0,9 3,1 0,9 3,1 3,3 2,8 2,8 2,5 4,0 4,3 1,1 2,1 3,8 4,6 3,8 2,3 3,9 2,4 4,1 4,2
10.4. Длина североморской камбалы (в см) в возрасте от 10 до 15 лет имеет значения:
48,1 47,8 48,1 49,7 54,1 48,4 48,7 47,4 50,0 48,3
49,9 52,2 52,3 50,3 51,7 44,6 51,5 53,6 51,2 50,1
50,9 48,2 51,3 49,3 48,5 52,6 50,4 49,8 50,5 49,2
45,8 50,2 49,5 47,6 50,5 49,2 47,3 49,1 47,1 47,2
52,1 46,4 51,4 52,4 49,9 48,6 55,6 52,8 54,7 47,6
49,4 49,5 44,0 49,5 52,5 51,8 45,2 48,8 50,8 50,3
51,7 50,8 50,2 51,2 46,8 47,5 50,7 52,4 47,2 49,6
50,1 49,3 47,4 51,2 51,6 49,6 49,3 49,4 52,7 51,1
Числовые характеристики выборочной
Совокупности
Числовыми характеристиками случайного признака в выборке являются:
1) выборочная средняя 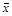 (выборочный начальный момент первого порядка
(выборочный начальный момент первого порядка 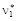 ):
):
 или
или  ; (10.1)
; (10.1)
2) выборочная дисперсия  (выборочный центральный момент второго порядка
(выборочный центральный момент второго порядка 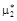 ):
):
 или
или  (10.2)
(10.2)
3) выборочное среднее квадратичное отклонение
 (10.3)
(10.3)
4) модой Мо эмпирического распределения называется значение признака, обладающего наибольшей частотой;
для интервального вариационного ряда
 (10.4)
(10.4)
где  - нижняя граница модального интервала,
- нижняя граница модального интервала,
 - частоты модального, предмодального и послемодального интервалов,
- частоты модального, предмодального и послемодального интервалов,
h - ширина интервала (шаг ряда);
5) медианой Ме эмпирического распределения называется значение случайного признака, делящего выборочную совокупность на две равновеликие части; для дискретного ряда медиана равна  или
или 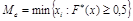 , для интервального -
, для интервального -
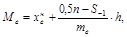 (10.5)
(10.5)
где 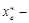 нижняя граница медианного интервала, определяемого по вы-
нижняя граница медианного интервала, определяемого по вы-
шеуказанному правилу;
n - объем выборки;
me - частота медианного интервала;
S-1 - накопленная частота интервала, предшествующего медианному;
6) коэффициент вариации V =  (10.6)
(10.6)
7) асимметрия и эксцесс эмпирического распределения

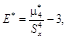 (10.7)
(10.7)
где выборочные центральные моменты  определяются через начальные моменты случайной величины соотношениями
определяются через начальные моменты случайной величины соотношениями
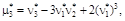

В задачах 10.5 – 10.7 вычислить характеристики выборочной совокупности (среднее значение случайного признака, дисперсию, среднее квадратическое отклонение, моду, медиану, коэффициент вариации, асимметрию и эксцесс).
10.5.
| Интервалы | 5 – 7 | 7 – 9 | 9 – 11 | 11 – 13 | 13 – 15 | 15 – 17 |
| Частоты | 8 | 14 | 40 | 26 | 6 | 4 |
10.6.
| Интервалы | 10 – 14 | 14 – 18 | 18 – 22 | 22 – 26 | 26 – 30 | 30 – 34 |
| Частоты | 1 | 5 | 10 | 20 | 18 | 3 |
10.7.
| Интервалы | 2 – 4 | 4 – 6 | 6 – 8 | 8 – 10 | 10 –12 | 12 –14 |
| Частоты | 10 | 20 | 10 | 8 | 4 | 1 |
В том случае, когда значения случайного признака в выборке выражены большими числами, затрудняющими процедуры вычислений, можно использовать линейное преобразование вида
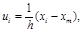 (10.8)
(10.8)
где h – шаг ряда (ширина интервала),
xm - мода выборочного распределения.
Преобразование вносит в выборку систематическую ошибку xm , при этом результат подвергается преобразованию масштаба с коэффициентом 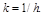 В итоге новые варианты u1, u2, …, un можно рассматривать как выборку из генеральной совокупности
В итоге новые варианты u1, u2, …, un можно рассматривать как выборку из генеральной совокупности  Тогда выборочные моменты случайной величины Х определяются через соответствующие моменты случайной величины U следующим образом:
Тогда выборочные моменты случайной величины Х определяются через соответствующие моменты случайной величины U следующим образом:
 в частности,
в частности,  откуда следует, что
откуда следует, что 
10.8. Вычислить  для данной выборки.
для данной выборки.
| Интервалы | 134-138 | 138-142 | 142-146 | 146-150 | 150-154 | 154-158 |
| Частоты | 1 | 3 | 15 | 18 | 14 | 2 |
¢ Преобразуем интервальный ряд в дискретный, взяв в качестве дискретных значений xi признака середины интервалов. Одновременно преобразуем случайную величину Х в случайную величину U при h = 4 и xm = 148. Составим рабочую таблицу (10.3).
Таблица 10.3
| xi | mi | ui | ui mi | 
| 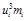
| 
|
| 136 | 1 | - 3 | - 3 | 9 | - 27 | 81 |
| 140 | 3 | - 2 | - 6 | 12 | - 24 | 48 |
| 144 | 15 | -1 | - 15 | 15 | - 15 | 15 |
| 148 | 18 | 0 | 0 | 0 | 0 | 0 |
| 152 | 14 | 1 | 14 | 14 | 14 | 14 |
| 156 | 2 | 2 | 4 | 8 | 16 | 32 |

| 53 | - 6 | 58 | - 36 | 190 |
Заполнив таблицу, вычисляем выборочные начальные моменты «условного» признака U:
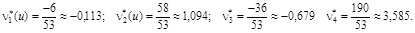
Далее находим выборочные центральные моменты признака U .
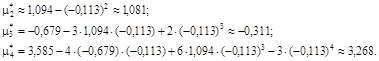
Наконец, определяем искомые характеристики выборки:
 £
£
Дата добавления: 2020-11-23; просмотров: 125; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!