Теодолитная съемка. Способы съемки ситуации.
Вопросы для изучения:
1. Теодолитная съемка. Назначение планового съемочного обоснования. Его виды.
2. Теодолитные ходы. Обработка результатов измерений в теодолитном ходе.
3. Теодолитная съемка. Способы съемки ситуации.
4. Составление контурного топографического плана.
Вопросы и задания для закрепления:
1. Какова цель и назначение создания планового съемочного обоснования?
2. Назовите виды теодолитных ходов. С какой целью их прокладывают?
3. Какие методы измерения длин сторон и углов применяют в теодолитных ходах?
4. Какие записи ведут при выполнении теодолитных съемок?
5. Назовите последовательность вычислений в ведомости координат.
6. Какой постграничный контроль предусмотрен при обработке результатов измерений.
Используемая литература
1. Григоренко А.Г., Киселев М.И. Инженерная геодезия: учебник для техникумов. – 2-е изд., перераб. и доп.- М.: Высш. шк.,1983. Стр.114-124.
2. Лошкарев Н.А. Геодезия: учеб. пособие для техникумов. – Л.: Стройиздат, Ленингр. отд-ние, 1986. Стр.67-75.
3. Нестеренок М.С., Нестеренок В.Ф.. Позняк А.В. Геодезия: Учебник. Мн.: Универси-тетское, 2001. Стр.121-134,143-146, 151-154.
Ответы
1. Теодолитная съемка. Назначение планового съемочного обоснования. Его виды.
Геодезическое съемочное обоснование служит для передачи координат от пунктов плановых и высотных сетей на участок топографической съемки, перенесения на местность проектов инженерных сооружений. Пункты съемочного обоснования закрепляют постоянными знаками на застроенной территории (постоянное съемочное обоснование) — центрами, заложенными в грунт, в углы капитальных зданий, и стержнями с головкой — в асфальтовое покрытие. На незастроенной территории, как правило, применяются временные знаки — деревянные столбы, колья, металлические трубки, стержни и т.п.
|
|
|
В открытой местности съемочное обоснование можно создавать микротриангуляцией в виде сети треугольников с длиной сторон не менее 150 м, углами не меньше 20° и не больше 160°. Базисные стороны сети измеряют с относительной погрешностью 1/5000, а углы в треугольниках — с погрешностью mβ = 0,5', допустимая невязка измеренных углов в каждом треугольнике равна 1,5'. Примером сети микротриангуляции служит цепочка треугольников (рис. 1, а), опирающихся на стороны АВ и СО геодезической опорной сети.
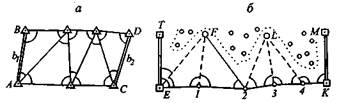
Рис.1. Цепочка микротриангуляции и угловые запечки
Плановые координаты пунктов F и L, (рис.1,б) получают прямыми геодезическими засечками относительно полигонометрического хода, координаты точек которого известны.
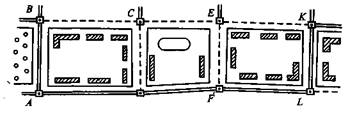
Рис. 2. Четырехугольники без диагоналей
На застроенных территориях с приблизительно прямоугольной системой улиц координаты пунктов съемочной сети можно получить методом четырехугольников без диагоналей, в которых измеряют все четыре угла (рис.2). В исходных четырехугольниках измеряют две стороны, а в остальных — только одну.
|
|
|
Теодолитные ходы. Обработка результатов измерений в теодолитном ходе.
Теодолитные ходы прокладывают для развития съемочного обоснования в населенных пунктах на местности, покрытой высокой растительностью, на небольших открытых площадях.
Теодолитным ходом называют полигонометрический ход, в котором углы между сторонами измеряют техническим теодолитом, а стороны — землемерными лентами, рулетками или оптическими дальномерами равной им точности (относительная погрешность 1/ Т = 1/1000 — 1/3000).
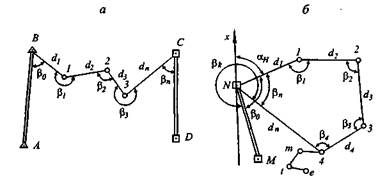
Рис. 3. Схема теодолитных ходов:
а — разомкнутого; 6 — замкнутого
Различают разомкнутый и замкнутый теодолитные ходы.
Разомкнутый теодолитный ход (рис.3, а) опирается на исходные пункты В и С геодезической сети, замкнутый (рис. 3, б) — может опираться на исходный пункт одной вершиной. Висячий теодолитный ход 4 – m – t - е (см. рис. 3, б) допускается как исключение в сложной ситуации.
Теодолитные ходы прокладывают с учетом их дальнейшего использования для съемки местности, поэтому до начала полевых работ составляют проект теодолитных ходов на имеющемся плане более мелкого масштаба или на глазомерно составленном чертеже местности. В процессе рекогносцировки (детального осмотра местности) уточняют составленный проект и окончательно выбирают местоположение вершин съемочного обоснования, затем закрепляют их временными или постоянными знаками.
|
|
|
Длины сторон теодолитного хода должны быть не менее 20 м и не более 350 м.
Плановые координаты пунктов съемочного обоснования определяются относительно пунктов государственной геодезической сети или сетей сгущения с погрешностью, которая не должна превышать 0,2 мм в масштабе плана на открытой или застроенной местности и 0,3 мм в масштабе плана на местности, покрытой кустарником или лесом (закрытой местности). Поэтому длины теодолитных ходов ограничивают в зависимости от масштаба предстоящей топографической съемки и относительной точности измерения сторон хода 1/Т (табл. 1).
Таблица 1 Технические требования к теодолитным ходам
| Масштаб топографической съемки | Открытая местность, застроенная территория | Закрытая местность
| |||||||
| 1/Т 1/3000 | 1/Т 1/2000 | 1/Т 1/1000 | Висячий ход | 1/Т 1/2000 | 1/Т 1/1000 | Висячий ход | |||
Допустимая длина теодолитного хода, км
| 1:5000 | 6,0 | 4,0 | 2,0 | 0,35 | 6,0 | 3,0 | 0,5 |
| 1:2000 | 3,0 | 2,0 | 1,0 | 0,2 | 3,6 | 1,5 | 0,3 |
| 1:1000 | 1,8 | 1,2 | 0,6 | 0,15 | 1,5 | 1,5 | 0,2 |
| 1:500 | 0,9 | 0,6 | 0,3 | 0,1 | - | — | - |
Измерение углов и сторон. В теодолитных ходах чаще всего измеряют правые по ходу углы теодолитом ТЗО двумя полуприемами с соблюдением технических мер по устранению погрешностей, рассмотренных в теме 2.1. Длины сторон измеряют в прямом и обратном направлении. Техника измерений предусматривает устранение грубых и уменьшение систематических погрешностей. При вычислении горизонтального проложения измеренных расстояний учитываются поправки за компарирование, температуру и наклон (см. тему 2.2.).
Привязка теодолитного хода к исходным пунктам геодезической сети. Рассмотрим следующие случаи привязки.
Случай 1. Теодолитный ход В-1 ... 3-С (рис. 3, а) опирается на пункты В и С геодезической сети. В этом случае необходимо измерить правые по ходу примычные углы βo и βn на начальном и конечном пунктах, откуда видны соседние пункты А и D опорной геодезической сети. Замкнутый теодолитный ход на рис. 3, б опирается на пункт N полигонометрической сети. Для привязки хода к геодезической сети в вершине N измеряют примычный угол βo начальной стороны N—M и примычный угол βk для конечной стороны 4-N.
Случай 2. Замкнутый теодолитный ход проложен вокруг объекта съемки на некотором удалении от пунктов исходной геодезической сети. Для его привязки прокладывают не менее двух привязочных теодолитных ходов между опорными пунктами и вершинами замкнутого хода с измерением всех примычных углов.
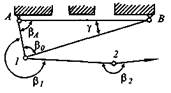
Рис.4. Привязка теодолитного хода к стенным пунктам
Случай 3. Исходные пункты А и В закреплены на стенах зданий (рис.4). Для привязки точки 1 хода измеряют расстояния 1А и 1В, а также внутренний угол βo треугольника А1В и внешний угол β1 . По известным координатам пунктов А и В, решая обратную геодезическую задачу, вычисляют длину линии АВ и ее дирекционный угол α1. Из треугольника А1В по теореме синусов находят углы βА , γ и длины SA, SB сторон А-1 и В-1 соответственно, тогда дирекционный угол стороны А-1 будет равен αA = α1 + β1 , стороны В-1 – αВ = α1 + 180° - γ. По найденным значениям длины и дирекционного угла сторон А-1 и В-1 можно вычислить координаты точки 1 относительно пункта А и для контроля — относительно пункта В по формулам прямой геодезической задачи. Через примычный угол β1 вычисляется дирекционный угол линии 1—2 теодолитного хода.
Результаты полевых измерений по прокладке теодолитных ходов записывают в специальном полевом журнале. В камеральных условиях проверяют записи, повторно вычисляют углы, длины сторон, затем в измеренные расстояния вводят поправки за компарирование, наклон и температуру. Для последующих вычислений составляют пояснительную схему теодолитных ходов в произвольном масштабе, на которой указывают величины измеренных углов и горизонтальных расстояний.
Угловая невязка замкнутого теодолитного хода. Для вычисления угловой невязки суммируют все внутренние измеренные правые по ходу углы замкнутого хода (см. рис. 3, б), исключая примычные, и вычисляют теоретическую сумму внутренних углов хода, представляющего собой n-вершинный многоугольник ∑βтеор = 180° (п - 2).
Разность ƒβ суммы измеренных углов β' и теоретической суммы углов замкнутого многоугольника, равной 180°×(n — 2), называют угловой невязкой хода, т.е.
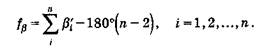 (1)
(1)
Если бы измеренные углы β' получали без погрешностей, то невязка ƒβ равнялась бы нулю. Практически величина ƒβ характеризует качество измерения углов. Допустимая угловая невязка вычисляется по формуле
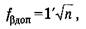 (2)
(2)
Допустимая погрешность Δ∑ пред обозначена через ƒβ доп , удвоенная погрешность измерения угла 2m = 1'.
Фактическая невязка ƒβ не должна превышать допустимой величины, в противном случае необходимо проверить результаты вычислений и измерений и устранить грубые погрешности в значениях β'i.
Уравнивание измеренных углов. Если угловая невязка допустима, измеренные углы β'i уравнивают, т.е. между ними приблизительно поровну распределяют фактическую невязку ƒβ, разбитую на поправки, противоположные по знаку невязке:
 (3)
(3)
и округленные до 0,1'. Причем сумма поправок должна равняться невязке с обратным знаком, т.е.
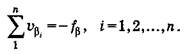 (4)
(4)
Поправки υβi прибавляют к измеренным углам β'i:
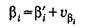 (5)
(5)
и этим их уравнивают (упрощенным способом). Сумма уравненных углов должна равняться теоретической сумме.
Пример 1. Определить угловую невязку, ее допустимую величину, если в замкнутом теодолитном ходе с тремя вершинами измерены углы, значения которых β'1 = 30° 01', β'2= 59° 59' и β'3 = 90° 01'. Уравнять измеренные углы.
Решение. Найдем угловую невязку ƒβ = 180° 01' - 180° 00' = = +0° 01'; ƒβдоп = 1׀ √3= 1,7'; получим поправки υi = -1' /3 = = -0,333 и округлим υ1 = - 0,3'; υ2= - 0,3'; υ3= - 0,4'; при этом
∑ υi = -1'. Уравненные углы β'1 = 30° 00,7'; β'2= 59° 58,7'; β'3 = 90° 00,6'. Их сумма будет равна 180° 00'.

Рис. 5. Дирекционные углы сторон и координаты вершин теодолитного хода
Угловая невязка разомкнутого теодолитного хода. В разомкнутом теодолитном ходе (рис. 5), опирающемся на исходные геодезические пункты В (триангуляции) и С (полигоно-метрии), измерены примычные углы β1 и βn, являющиеся правыми по ходу, как и углы β2, β3..., βn-1 между сторонами хода. Число n измеренных углов на единицу больше числа n—1 сторон. Предположим, что измеренные углы β'i; после уравнивания получили значения βi. Зная начальный дирекционный угол αн стороны АВ триангуляции и примычный угол βi, найдем дирекционный угол α1 стороны хода В-1. Согласно рис.5 при вершине В сумма углов α1+ β1 = αн + 180°, при вершине 1 — α2+ β2 = α1 + 180° и т.д. Отсюда получим:
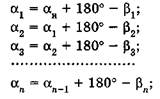 (6)
(6)
Обобщив выражение (6), можно записать
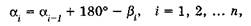 (7)
(7)
т.е. дирекционный угол следующей стороны равен дирекционному углу предыдущей плюс 180°, минус правый по ходу угол между этими сторонами теодолитного хода. Используя формулы (6), находим
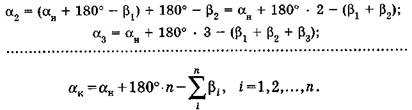
Из последнего соотношения найдем теоретическую сумму углов разомкнутого теодолитного хода:
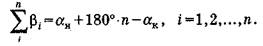
Поскольку измеренные правые по ходу углы βi содержат погрешности Δβi, сумма измеренных углов не равна их теоретической сумме на величину невязки:
 (8)
(8)
Допустимая угловая невязка теодолитного хода ƒβдоп= 1' √n.Уравнивают измеренные углы разомкнутого хода так же, как и замкнутого.
Если в теодолитном ходе измерены левые по ходу углы, то формулы (7) и (8) примут вид
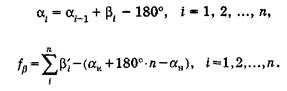 (10)
(10)
Правые измеренные „углы теодолитного хода β΄i записаны в табл.2, вычислены Σβ΄i и
Σβтеор = 111° 50,8' + 180° • 5 - 260° 50,8' = 751° 00,0', указаны ƒβ и ƒβдоп, поправки к углам и
уравненные углы.
Дирекционные углы сторон теодолитного хода последовательно вычисляют по формуле (7), начиная от αn , и при отсутствии погрешностей в вычислениях получают значения αk. Результаты вычислений даны в графе 4 табл. 2. Румбы находят по формулам, приведенным в табл. 1, и записывают в графе 5.
Вычисление погрешностей и оценка точности теодолитного хода. В графе 6 табл. 2 записывают длины di сторон теодолитного хода в горизонтальном проложении, рассчитан-ные с учетом поправок за компарирование, наклон и температуру. Приращения координат Δх΄i и Δу΄i. находят по формулам (1, см.тема 1.1.) и записывают в таблице со знаком "плюс" или "минус" соответственно направлению стороны и. (см. рис.7, см.тема 1.1.). При учебных вычислениях пользуются микрокалькуляторами или таблицами приращений координат, результаты вычислений округляют до 0,01 м.
Согласно рис.5 приращения координат Δх΄i и Δу΄i представляют собой проекции сторон di на оси абсцисс и ординат, а теоретические суммы таких проекций:
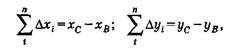 (11)
(11)
где хс – хв и ус – ув - разности координат конечного и начального исходных пунктов.
Вследствие погрешностей в значениях дирекционных углов αί  и сторон di вычислен-ные приращения Δх΄i и Δу΄i. и их суммы ∑Δх΄i и ∑Δу΄i также содержат погрешности, поэтому условие (11) точно не выполняется. Разности координат конечного хк и ук и начального хн и ун исходных хк — хн, ук — ун пунктов представляют собой теоретические суммы приращений координат, т.е.
и сторон di вычислен-ные приращения Δх΄i и Δу΄i. и их суммы ∑Δх΄i и ∑Δу΄i также содержат погрешности, поэтому условие (11) точно не выполняется. Разности координат конечного хк и ук и начального хн и ун исходных хк — хн, ук — ун пунктов представляют собой теоретические суммы приращений координат, т.е.
∑Δхтеор = хк — хн ; ∑Δутеор = ук — ун . Расхождения в суммах вычисленных и теоретических приращений координат называются невязками ƒх и ƒу приращений координат:
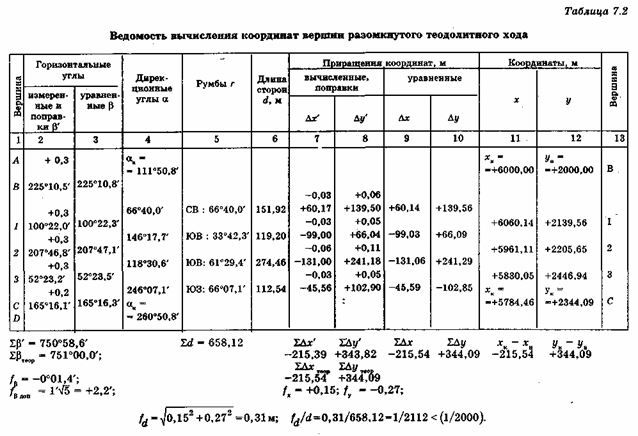
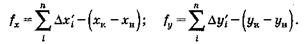 (12)
(12)
Величины ƒх и ƒу являются катетами прямоугольного треугольника погрешностей
 (рис.6), гипотенуза которого СС' = ƒd называется линейной или абсолютной невязкой теодолитного хода:
(рис.6), гипотенуза которого СС' = ƒd называется линейной или абсолютной невязкой теодолитного хода:
 (13)
(13)
По формулам обратной геодезической задачи (3), (4, см.т. 1.1.) можно определить румб и дирекционный угол линейной невязки ƒd.
Рис..6. Абсолютная линейная невязка
Относительная невязка теодолитного хода выражается дробью с единицей в числителе, равной отношению невязки ƒd к длине хода ∑di, т.е.
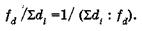 (14)
(14)
Допустимая относительная невязка хода определяется погрешностями линейных и угловых измерений: для благоприятных условий местности — 1:3000, для средних (небольшие неровности, местами трава) — 1:2000, для неблагоприятных (рыхлый грунт, заросли травы и т.д.) — 1:1000. Допустимая абсолютная невязка для этих же условий
ƒd доп = ∑di / 3000; ƒd доп = ∑di / 2000; ƒd доп = ∑di / 1000 соответственно (см. табл. 2).
В нашем примере (см. табл.2) подсчитаны значения всех величин, необходимых для вычисления невязок, найдены фактическая линейная невязка хода ƒd, относительная невязка ƒd/∑di = 1/2112 и показано, что ее величина меньше допустимой относительной невязки 1/2000.
Уравнение приращений координат. Если фактическая невязка хода ƒd допустима, то к вычисленным приращениям координат Δх΄i и Δу΄i добавляют поправки υхi и υуi, представ-ляющие собой части невязок ƒх и ƒу , пропорциональные длинам di сторон хода, а знак поправок противоположен знаку соответствующих невязок:
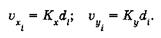 (15)
(15)
В формулах (15) Кх и Ку — коэффициенты пропорциональности:
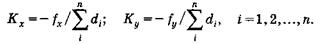 (16)
(16)
Поправки проверяются по условию равенства их суммы соответствующей невязке, взятой с обратным знаком:
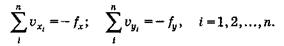 (17)
(17)
Уравненные приращения координат находят путем прибавления к вычисленным приращениям соответствующих поправок:
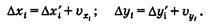 (18)
(18)
В нашем примере над значениями Δх΄i и Δу΄i указаны поправки υхi и υуi (см. табл. 2, графы 7 и 8). Для них Кх = - (+0,15) : 658,12 = 0,000 224; υхi = Кх × d1 = Кх ·151,92 = -0,03 м; υх2 = Кх ·119,2 = - 0,03 м и т.д. Сумма поправок υхi равна невязке ƒх с обратным знаком, т.е. ∑υхi = - ƒх = 0,15. В графе 9 записаны уравненные приращения Δхί и их сумма ∑Δхί = — 215,54, которая совпала с разностью хк — хн.
Вычисление координат. Координаты хί и уί вершин теодолитного хода последовательно вычисляются по формулам
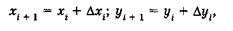 (19)
(19)
т.е. абсцисса хί и ордината уί следующей вершины равны абсциссе и ординате хί-1 и уί-1 предыдущей вершины плюс соответствующие уравненные приращения координат Δхi и Δуi
Для контроля в конце вычислений получают значения хк и ук, которые должны равняться исходным, тогда результаты, записанные в графах 7, 8, 9 и 10 (табл. 2), будут найдены без погрешностей.
Замкнутый теодолитный ход. Пункт N стороны NМ полигонометрии (см. рис.3, б) служит исходным для замкнутого теодолитного хода N-1, ..., 4- N. Для определения дирекционного угла αн первой стороны хода N-1 измеряется примычный угол β0, а для контроля — примычный правый по ходу угол βк конечной стороны 4- N хода. В целом вычисления в координатной ведомости аналогичны расчетам для разомкнутого теодолитного хода.
Пример 1. Вычислить координаты вершин замкнутого теодолитного хода, если исходный дирекционный угол стороны N-М полигонометрии αn=154°40', измеренные значения при-мычных углов β0 = 100°09,5'; βк = 328°29,5', внутреннего угла теодолитного хода βn = 68°40'.
Р е ш е н и е. Вначале по этим данным находим дирекционный угол α1 первой стороны N-1 теодолитного хода. Согласно рис.3, б α1 = αн - β0 = 154°40' - 100°09,5' = 54°30,5';
контроль: α1 = αн + βк - βп = 154°40' + 328°29,5' - 68°40' = 414°29,5', или α1 = 414°29,5' - 360° = 54°29,5'. Поскольку допустимо расхождение величин угла α1 (он же является начальным дирекционным углом), за окончательный результат принимаем среднее α1 = 54°30'. Значение αн = α1 записываем в координатную ведомость (табл.3, графа 4).
В графе 2 записаны значения измеренных правых по ходу внутренних углов β'i замкнутого хода, их сумма ∑β'i и теоретическая сумма углов βi = 180° (п - 2). Невязка ƒβ, ее допустимая величина, поправки в измеренные углы и уравненные углы расчитаны по формулам (1)— (5). Сумма уравненных углов ∑βi = 540°00' равна их теоретической сумме.
В графе 4 записаны значения дирекционных углов, последовательно вычисленных по формуле (7) с контролем по значению исходного дирекционного угла α1 = αн = αк стороны
N-1 теодолитного хода. Вычисленные приращения координат Δх'i и Δу'i записаны со своим знаком, подсчитаны их суммы. Поскольку пункт N с известными координатами хн, yн в данном случае является и начальным и конечным, в формулах (12) хк - хн = 0 и ук – ун = 0, т.е. в замкнутом теодолитном ходе теоретические суммы приращений координат равны нулю, а невязки вычисленных приращений - соответствующим суммам вычисленных приращений:
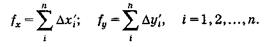 (20)
(20)
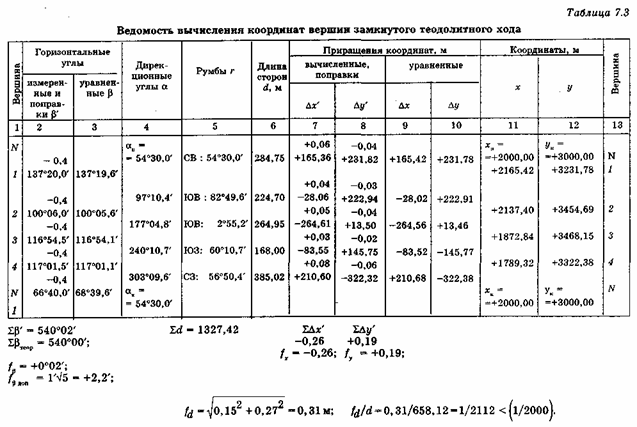
В нашем примере абсолютная линейная невязка хода ƒd = 0,32 см, относительная величина этой невязки ƒd/Σdi = 1/4148 удовлетворяет допустимой относительной невязке 1/2000. Поправки υ xi , υу i к вычисленным значениям Δх'i и Δу'i найдены по формулам (15), (16), суммы поправок проверены по формулам (17). Уравненные координаты получены по формулам (18), а искомые координаты вершин хода — по формулам (19).
НАЗЕМНЫЕ ТОПОГРАФИЧЕСКИЕ СЪЕМКИ
Теодолитная съемка. Способы съемки ситуации.
Топографической съемкой называется комплекс работ, выполняемых на местности и в камеральных условиях с целью получения топографической карты или плана, а также для получения топографических данных, например в цифровой форме.
Топографические планы и карты создаются в основном методами аэрофотосъемки, но на небольших по площади участках их получают наземными съемками — теодолитной, тахеометрической, мензульной, фототеодолитной и нивелированием поверхности.
Для разработки проектов строительства топографические планы составляют в соответствии с требованиями документа "Строительные нормы Республики Беларусь. СНБ 1.02.01.96. Инженерные изыскания для строительства". Мн., 1996 г. В этом документе для различных видов строительства указаны высота сечения рельефа и масштаб топографического плана. Так, при съемках масштаба 1:5000 применяют высоту сечения hc = 5,2 и 0,5 м; для планов масштаба 1:2000 - hc = 2,1 и 0,5 м; для планов масштаба 1:1000 и 1:500 — hc =1 или 0,5 м. Наименьшие высоты используют для изображения горизонталями слабовыраженного рельефа.
Топографическая съемка местности производится относительно пунктов съемочного обоснования, созданного теодолитными ходами, микротриангуляцией и угловыми засечками в сочетании с нивелированием.
Теодолитная съемка — это топографическая съемка, выполняемая при помощи теодолита, землемерных лент, рулеток или дальномеров. По своей точности дальномеры должны соответствовать точности измерения стальными лентами и рулетками. В результате теодолитной съемки получают контурный план местности. При необходимости теодолитная дополняется высотной съемкой этого же участка и на плане изображается рельеф местности. Теодолитная съемка производится относительно вершин и сторон теодолитных ходов съемочного обоснования (рис.7), при этом измеряют расстояния до контурных точек местности и углы, определяющие плановое положение этих точек, ведут абрис
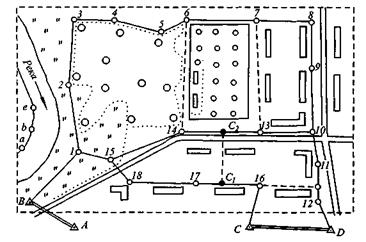
Рис. 7 . Схема съемочного обоснования
(схематическую зарисовку местных объектов с указаниями схем и числовых данных измерений).
Полевые работы включают рекогносцировку (геодезическое изучение) участка, закрепление вершин теодолитных ходов, измерение длины сторон и углов между сторонами ходов, съемку ситуации. В состав камеральных работ входят вычисления координат вершин теодолитных ходов, нанесение на план этих точек и ситуации по данным абрисов, вычерчивание плана условными топографическими знаками.
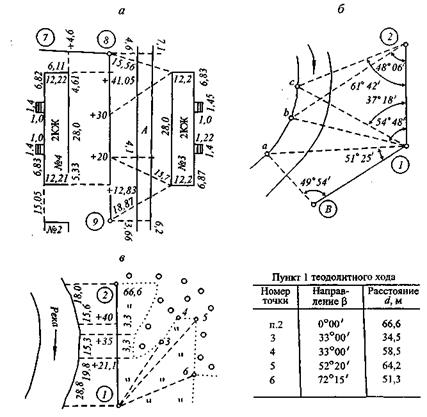 Способы съемки ситуации. В абрисах результаты съемки показывают в графической форме, отвечающей способу съемки ситуации. При способе перпендикуляров землемерную ленту помещают с помощью зрительной трубы теодолита в створе пунктов 9 и 8 теодолитного хода (рис. 8, а), совместив нуль ленты с точкой 9. Приложив нулевой штрих рулетки к углу дома № 4, на ленту опускают перпендикуляр и отсчитывают его длину по рулетке (5,33 м), по ленте — расстояние от точки 9 до основания перпендикуляра (+12,83). Перпендикуляры длиной до 4—8 м восстанавливают на глаз, более длинные — с применением экера. Ленту перемещают в створе стороны 9—8 теодолитного хода и определяют длину и положение других съемочных перпендикуляров. На абрисе указывают данные обмера контура здания по цоколю и его выступов, расстояния между соседними домами.
Способы съемки ситуации. В абрисах результаты съемки показывают в графической форме, отвечающей способу съемки ситуации. При способе перпендикуляров землемерную ленту помещают с помощью зрительной трубы теодолита в створе пунктов 9 и 8 теодолитного хода (рис. 8, а), совместив нуль ленты с точкой 9. Приложив нулевой штрих рулетки к углу дома № 4, на ленту опускают перпендикуляр и отсчитывают его длину по рулетке (5,33 м), по ленте — расстояние от точки 9 до основания перпендикуляра (+12,83). Перпендикуляры длиной до 4—8 м восстанавливают на глаз, более длинные — с применением экера. Ленту перемещают в створе стороны 9—8 теодолитного хода и определяют длину и положение других съемочных перпендикуляров. На абрисе указывают данные обмера контура здания по цоколю и его выступов, расстояния между соседними домами.
Рис. 8 . Абрисы съемки ситуации:
а — перпендикулярами и линейными засечками; б — угловыми засечками; в — полярным
способом
4. Составление контурного топографического плана
На план точки наносят с помощью угольников, масштабной линейки и циркуля-измерителя.
Углы дома № 3 (см. рис. 8, а) сняты линейными засечками: рулеткой измерены расстояния от опорных точек 9 и +20 теодолитного хода до одного из углов здания и аналогично от опорных точек +30 и 8 измерены расстояния до второго угла здания. На план их можно нанести циркулем-измерителем. Углы зданий окажутся в пересечении дуг с радиусами измеренных расстояний, взятых в принятом масштабе. Правильность нанесения углов зданий на план контролируется измерением длины фасада.
Применяя способ угловых засечек, на противоположном берегу реки ставят вехи в точках а, в, с (см. рис.8,б), теодолитом относительно опорных точек (пунктов съемочного обоснования) измеряют горизонтальные углы, а на плане эти точки находят при помощи транспортира в пересечениях сторон углов.
На абрисе (рис. 8, в) и в таблице к этому рисунку приведены данные съемки границы луга полярным способом. Полюс выбран в пункте 1 хода, горизонтальные углы βi (направления на точки) отсчитываются по горизонтальному кругу теодолита от полярного направления на пункт 2, расстояния измеряются дальномером или рулеткой.
Способ обхода состоит в том, что по границе застройки, пашни, леса и т. д. прокладывают теодолитный ход (ход 2-3-4-5-6 на рис. 7), затем по вычисленным координатам точки хода наносят на план и изображают соответствующими условными знаками контуры.
Тема 2.4. Плановое съемочное обоснование Теодолитная съемка.
Вопросы для изучения:
5. Теодолитная съемка. Назначение планового съемочного обоснования. Его виды.
6. Теодолитные ходы. Обработка результатов измерений в теодолитном ходе.
7. Теодолитная съемка. Способы съемки ситуации.
8. Составление контурного топографического плана.
Вопросы и задания для закрепления:
1. Какова цель и назначение создания планового съемочного обоснования?
2. Назовите виды теодолитных ходов. С какой целью их прокладывают?
3. Какие методы измерения длин сторон и углов применяют в теодолитных ходах?
4. Какие записи ведут при выполнении теодолитных съемок?
5. Назовите последовательность вычислений в ведомости координат.
6. Какой постграничный контроль предусмотрен при обработке результатов измерений.
Используемая литература
1. Григоренко А.Г., Киселев М.И. Инженерная геодезия: учебник для техникумов. – 2-е изд., перераб. и доп.- М.: Высш. шк.,1983. Стр.114-124.
2. Лошкарев Н.А. Геодезия: учеб. пособие для техникумов. – Л.: Стройиздат, Ленингр. отд-ние, 1986. Стр.67-75.
3. Нестеренок М.С., Нестеренок В.Ф.. Позняк А.В. Геодезия: Учебник. Мн.: Универси-тетское, 2001. Стр.121-134,143-146, 151-154.
Ответы
1. Теодолитная съемка. Назначение планового съемочного обоснования. Его виды.
Геодезическое съемочное обоснование служит для передачи координат от пунктов плановых и высотных сетей на участок топографической съемки, перенесения на местность проектов инженерных сооружений. Пункты съемочного обоснования закрепляют постоянными знаками на застроенной территории (постоянное съемочное обоснование) — центрами, заложенными в грунт, в углы капитальных зданий, и стержнями с головкой — в асфальтовое покрытие. На незастроенной территории, как правило, применяются временные знаки — деревянные столбы, колья, металлические трубки, стержни и т.п.
В открытой местности съемочное обоснование можно создавать микротриангуляцией в виде сети треугольников с длиной сторон не менее 150 м, углами не меньше 20° и не больше 160°. Базисные стороны сети измеряют с относительной погрешностью 1/5000, а углы в треугольниках — с погрешностью mβ = 0,5', допустимая невязка измеренных углов в каждом треугольнике равна 1,5'. Примером сети микротриангуляции служит цепочка треугольников (рис. 1, а), опирающихся на стороны АВ и СО геодезической опорной сети.

Рис.1. Цепочка микротриангуляции и угловые запечки
Плановые координаты пунктов F и L, (рис.1,б) получают прямыми геодезическими засечками относительно полигонометрического хода, координаты точек которого известны.
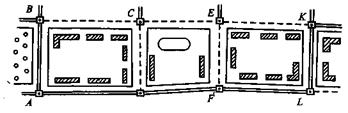
Рис. 2. Четырехугольники без диагоналей
На застроенных территориях с приблизительно прямоугольной системой улиц координаты пунктов съемочной сети можно получить методом четырехугольников без диагоналей, в которых измеряют все четыре угла (рис.2). В исходных четырехугольниках измеряют две стороны, а в остальных — только одну.
Дата добавления: 2020-11-23; просмотров: 441; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
