Задача 2 на доказательство пересечения прямой и плоскости
Занятие по математике № 29 Группа 2 ЖЗ Дата проведения: 28.10.20г.
Тема: Решение математических и прикладных задач.
Просмотреть видеофильм по ссылке: https://www.youtube.com/watch?v=JHyHaL5GIug
Теоретический материал для самостоятельного изучения
Повторение. Сложение векторов, умножение вектора на число
В окружающем мире мы встречаемся с такими величинами, для которых важен не только размер, но и направление. Такими величинами являются, например, сила и скорость. В математике такие величины описываются векторами.
Вектор – направленный отрезок.
Рис. 1. Вектор
Вектор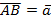 
(рис. 1).
Коллинеарными векторами называются такие векторы, которые лежат на параллельных прямых либо на одной прямой.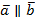 
(рис. 2).
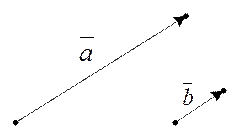
Рис. 2. Коллинеарные векторы
Можно ввести такое число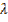 
, при котором 
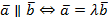(рис. 3). То есть умножением вектора на какое-либо число 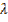, можно растянуть или сжать вектор.
Рис. 3. Умножение вектора на число
Если векторы коллинеарные и сонаправленные и их длины равны, то такие векторы называются равные: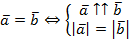 
.
Рассмотрим сложение векторов.
1. Правило параллелограмма (рис. 4).
Рис. 4. Сложение векторов
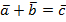
2. Правило треугольника (рис. 5).
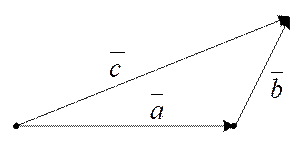
Рис. 5. Сложение векторов
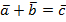
Векторы на плоскости
Рассмотрим векторы на плоскости. Для этого нам необходима пара неколлинеарных векторов (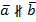 
).
Теорема: на плоскости любой вектор можно разложить по двум данным неколлинеарным векторам, причём коэффициенты разложения определяются единственным образом. То есть существует единственная пара чисел x и y, при которой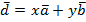 
(рис. 6).
|
|
|
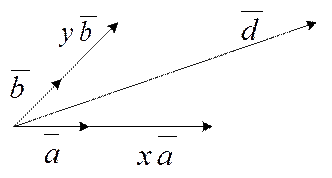
Рис. 6. Иллюстрация к теореме
Векторы в пространстве
Рассмотрим векторы в пространстве. Для этого необходимо выбрать три некомпланарных вектора ( 
.
Теорема: в пространстве любой вектор можно разложить по трём данным некомпланарным векторам, причём коэффициенты разложения определяются однозначно: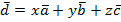 
. То есть вектор 
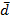однозначно разлагается по векторам 
, 
, 
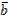с помощью чисел x, y, z (эта тройка чисел однозначная).
Объясним эту теорему (рис. 7). 
Рис. 7. Иллюстрация к объяснению теоремы
Проведём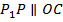 
, получим точку пересечения 
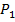с плоскостью 
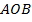. Следовательно, 
, но, по правилу параллелограмма,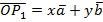 
, а так как вектор 
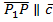, то 
. Поэтому .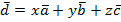
Закрепление знаний при решении задач.
Задача 1 на доказательство определённого соотношения отрезков
M – точка пересечения медиан в треугольнике ABC. Точка O – произвольная точка. Доказать, что 
.
Дано: M – точка пересечения медиан (рис. 8).
Доказать: .
Доказательство (1 способ)
Выразим OM через векторы:
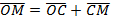
Складываем эти три соотношения: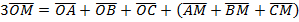 
.
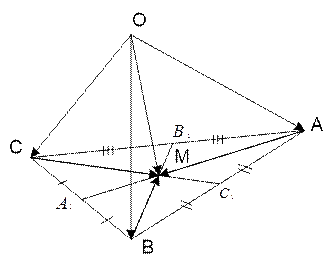
Рис. 8. Иллюстрация к задаче №1
|
|
|
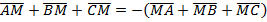
Докажем, что 
. По свойству, точка пересечения медиан треугольника рассекает каждую медиану в отношении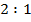 
, считая от вершины. То есть 
; 
; 
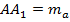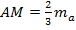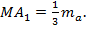Продлим медиану 
и отложим отрезок 
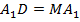(рис. 9).
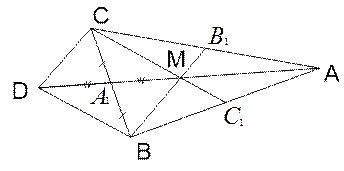
Рис. 9. Иллюстрация к задаче №1
Получили четырёхугольник MBDC. Его диагонали пересекаются и точкой пересечения делятся пополам, следовательно, MBDC – параллелограмм. Поэтому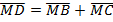 
.
, поэтому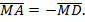 
Подставим эти данные в выражение 
, получим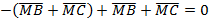 
.
Отсюда 
.
Что и требовалось доказать.
Доказательство (2 способ)
Выразим OM через вектор: .
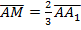- по свойству точки пересечения медиан треугольника.
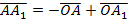
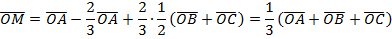
Что и требовалось доказать.
Задача 2 на доказательство пересечения прямой и плоскости
Дан параллелепипед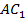 
(рис. 10). M – точка пересечения медиан в 
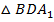. Доказать: 1) диагональ 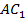пересечёт плоскость 
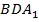в точке M; 2) 
.
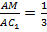Доказательство
Рис. 10. Иллюстрация к задаче №2
Вводим тройку некомпланарных векторов. Пусть ,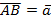 
, 
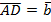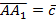, через эти векторы можно выразить все остальные нужные нам векторы: 
.
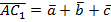Благодаря доказательству в задаче 1, знаем, что 
.
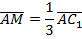
Вектор 
и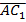 
коллинеарные, они имеют общую точку A, следовательно, точки A, M, 
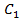лежат на одной прямой, поэтому прямая 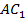пересекает плоскость 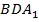в точке M ( 
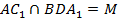). Что и требовалось доказать.
|
|
|
Отношение 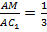. Что и требовалось доказать.
Дата добавления: 2020-11-23; просмотров: 63; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!