Как найти точку пересечения прямой и плоскости?
б) Найдём точку пересечения плоскости и прямой: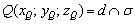 
. Не «Чёрный квадрат» Малевича, но тоже шедевр:
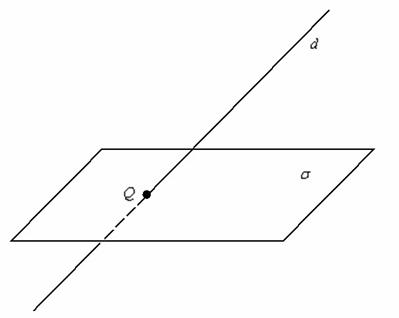
Приём решения стандартен и хорошо известен из статьи Задачи с прямой в пространстве. Сначала перепишем уравнения прямой в параметрической форме:
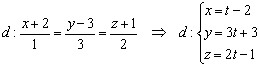
Точка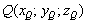 
принадлежит данной прямой, поэтому её координаты 
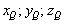при некотором значении параметра 
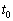удовлетворяют параметрическим уравнениям:
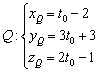, или одной строчкой: 
.
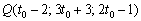С другой стороны, точка 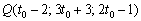принадлежит и плоскости 
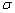, следовательно, координаты точки должны удовлетворять уравнению плоскости 
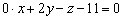, то есть должно выполняться равенство:
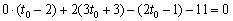– ну, или попросту параметрические координаты точки нужно подставить в уравнение плоскости.
Раскрываем скобки, приводим подобные слагаемые и находим «тэ нулевое»:
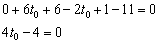
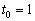– полученное значение параметра подставляем в параметрические выражения координат нашей точки:
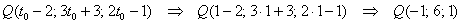
Интересно, что в данном пункте всё обошлось даже без векторов.
Чистка хвоста очевидна: координаты точки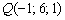 
должны «подходить» и в уравнения прямой и в уравнение плоскости. Проверку несложно выполнить устно.
в) Найдём уравнение плоскости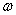 
, которая перпендикулярна плоскости 
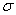и проходит через прямую 
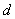. Задача весьма напоминает Пример № 12 урока Уравнение плоскости, в котором мы рассмотрели построение перпендикулярной плоскости, проходящей через две точки.
Выполним схематический чертёж:
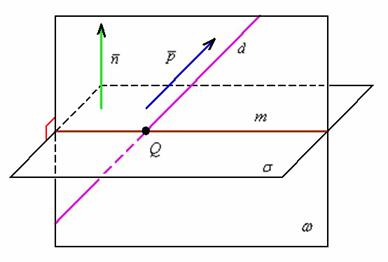
Уравнение плоскости 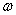можно составить по любой точке, которая принадлежит прямой 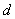, направляющему вектору 
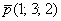прямой 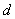и вектору нормали 
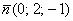плоскости .
|
|
|
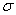В качестве точки, принадлежащей прямой «дэ», не возбраняется, конечно, взять найденную в предыдущем пункте точку пересечения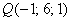 
, но в произвольной практической задаче она чаще всего не известна. Поэтому обычно используют самую «лёгкую добычу». В данном случае, очевидно, точку:
.
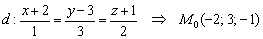Уравнение плоскости «омега» составим по точке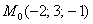 
и двум неколлинеарным векторам 
:
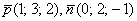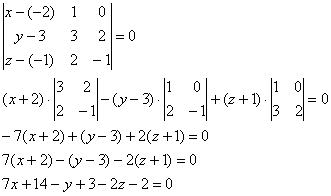
Таким образом: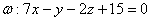 
Проверка опять же довольно простая. Устно находим скалярное произведение нормальных векторов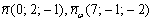 
двух плоскостей. Оно равно нулю, значит, плоскости перпендикулярны. На втором шаге нужно убедиться, что прямая «дэ» действительно лежит в найденной плоскости «омега». Можно использовать типовой алгоритм, рассмотренный в самом начале урока. Но тут есть другая возможность – устно подставляем координаты двух известных точек 
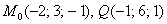в полученное уравнение плоскости 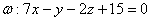. Обе точки «подходят», и это гарантирует, что и вся прямая 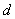лежит в плоскости .
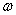Как найти уравнения проекции прямой на плоскость?
г) По умолчанию под проекцией понимается, как правило, ортогональная проекция. Что это такое и что это значит?
|
|
|
Физкульт-пятиминутка. Пожалуйста, найдите дома швабру или метлу и поместите её между своих ног. Подбородок плотно прижат к груди. Теперь строго перпендикулярно смотрим вниз на швабру..., при этом получается такое умное лицо…. Скрытая от вас часть пола – это и есть проекция швабры на плоскость. Да… …а я как погляжу, вы без комплексов =)
На чертеже наша «швабра» 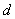проведена малиновым цветом, а её проекция, прямая 
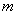– коричневым цветом. Легко заметить, что проекция задаётся пересечением плоскостей: 
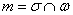, и на самом деле ответ уже готов:
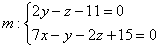
Другое дело, что часто требуется представить уравнения прямой в канонической форме. Это стандартная задача, рассмотренная в Примерах № 9, 10 урока Уравнения прямой в пространстве.
Точка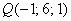 
, принадлежащая проекции, уже известна, осталось найти её направляющий вектор:
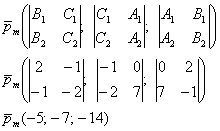
Таким образом, канонические уравнения проекции:
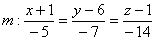
Обратите внимание, что на практике для решения данной задачи, в общем-то, не надо находить именно точку пересечения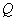 
(лишняя работа). Нас устроит любая точка, принадлежащая проекции. Красавица подбирается из системы 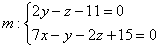(см. Примеры № 9, 10 урока Уравнения прямой в пространстве).
Есть и другой способ нахождения проекции, связанный с построением перпендикуляра к плоскости «сигма», но, я тут прикинул, он вряд ли короче. Однако на всякий случай озвучу алгоритм, вдруг понадобится кому:
|
|
|
– находим точку пересечения прямой и плоскости: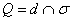 
(вот в этом способе уже обязательно находим);
– из произвольной точки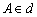 
(не совпадающей с точкой 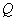) опускаем перпендикуляр 
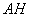на плоскость 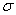(см. следующие параграфы);
– основание перпендикуляра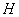 
находим как пересечение прямой 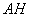и плоскости ;
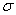– составляем канонические уравнения проекции 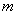по двум точкам: 
.
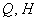Дата добавления: 2020-11-23; просмотров: 236; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!