Основные задачи на прямую и плоскость
Аналитическая геометрия на плоскости. Задачи на прямую.
Аналити́ческая геоме́трия — раздел геометрии, в котором геометрические фигуры и их свойства исследуются средствами алгебры.
В основе этого метода лежит так называемый метод координат, впервые применённый Декартом в 1637 году. Каждому геометрическому соотношению этот метод ставит в соответствие некоторое уравнение, связывающее координаты фигуры или тела. Такой метод «алгебраизации» геометрических свойств доказал свою универсальность и плодотворно применяется во многих естественных науках и в технике[1]. В математике аналитическая геометрия является также основой для других разделов геометрии — например, дифференциальной, алгебраической, комбинаторной и вычислительной геометрии.
Аналитическая геометрия на плоскости
Основные формулы
· Расстояние между точками A(x 1 , y 1 ) и B(x 2 , y 2 )
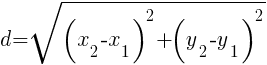
· Координаты точки С(x, y), которая делит отрезок, соединяющий точки A (x 1 , y 1 ) и B (x 2 , y 2 ), в отношении 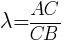
 , λ ≠ -1
, λ ≠ -1
· Координаты середины отрезка АВ
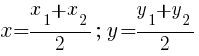
· Условие принадлежности трёх точек (x 1 , y 1 ), (x 2 , y 2 ), (x3, y3) одной прямой
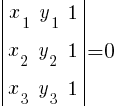
· Площадь треугольника с вершинами (x 1 , y 1 ), (x 2 , y 2 ), (x3, y3) (знак выбирается так, чтобы площадь была неотрицательной)

Прямая на плоскости
· Общее уравнение прямой
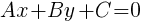
· Уравнение прямой, проходящей через точку (x 0 , y 0) перпендикулярно нормальному вектору {A;B}

· Каноническое уравнение прямой, проходящей через точку (x 0 , y 0) параллельно вектору {l;m}

|
|
|
Параметрические уравнения прямой, проходящей через точку (x 0 , y 0) параллельно вектору {l;m}
 , t ∈ (-∞, ∞)
, t ∈ (-∞, ∞)
Уравнение прямой, проходящей через две заданные точки (x 1 , y 1 ) и (x 2 , y 2 )

Уравнение прямой с угловым коэффициентом k, где  — угол наклона прямой к оси Оx
— угол наклона прямой к оси Оx
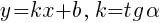
Уравнение прямой в отрезках, где (a;0) и — координаты точек пересечения прямой с осями Оx и Оy
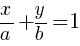 , a ≠ 0, b ≠ 0
, a ≠ 0, b ≠ 0
Нормальное уравнение прямой, где р — расстояние от начала координат до прямой, α — угол между осью Оx и перпендикуляром к прямой, проходящим через начало координат

Нормальный вид общего уравнения прямой; знак нормирующего множителя противоположен знаку С

Расстояние от точки (x 0 , y 0) до прямой Ax+By+C=0
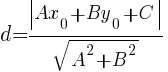
Координаты точек пересечения двух прямых
A 1 x+B 1 y+C 1 =0 и A 2 x+B 2 y+C 2 =0

Координаты точек пересечения прямых y=k 1 x+b 1 и y=k 2 x+b 2

· Условия параллельности прямых, заданных в общем виде A 1 x+B 1 y+C 1 =0, A 2 x+B 2 y+C 2 =0 и в виде y=k 1 x+b 1, y=k 2 x+b 2
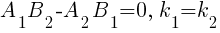
· Условия перпендикулярности прямых, заданных в общем виде A 1 x+B 1 y+C 1 =0, A 2 x+B 2 y+C 2 =0 и в виде y=k 1 x+b 1, y=k 2 x+b 2
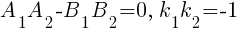
· Острый угол α между двумя прямыми, заданными в общем виде A 1 x+B 1 y+C 1 =0, A 2 x+B 2 y+C 2 =0 и в виде y=k 1 x+b 1, y=k 2 x+b 2
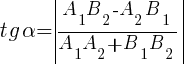 ,
,
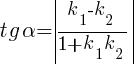 ,
,
k 1 k 2 ≠ -1, 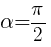 , если k 1 k 2 = -1.
, если k 1 k 2 = -1.
|
|
|
Предметом аналитической геометрии являются кривые и поверхности, которые изучаются при помощи алгебры. В основе исследований лежит метод координат, который определяет положение точки в пространстве с помощью чисел — координат этой точки. Каждая кривая или поверхность описывается одним или несколькими уравнениями, связывающими координаты точки, принадлежащей данному объекту. Геометрические свойства кривых или поверхностей описываются также уравнениями, связывающими координаты с некоторыми постоянными величинами — параметрами, которые в свою очередь определяют положение, форму, размер и другие характеристики объектов. Эти факты позволяют изучать геометрические объекты аналитическим (и в частности алгебраическим) методом.
При изучении геометрических объектов мы будем опираться на понятие вектора. Векторная величина характеризуется не только числовым значением, но и направлением в пространстве. Естественным изображением вектора служит направленный отрезок со стрелкой на одном из концов.
Основные задачи на прямую и плоскость
Данная задача прям таки вертится в умах человечества, и встречается в практических задачах чаще всего. Когда я приступил к разработке пространственной геометрии, то, начиная с урока Уравнение плоскости, мне даже было немного неловко, что посетители сайта обманывались в своих ожиданиях. Многие задачи уже были, а вот этой ещё нет….
|
|
|
Рассмотрим прямую  , которая пересекает плоскость
, которая пересекает плоскость 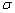 . Требуется найти точку, в которой прямая пересекает плоскость:
. Требуется найти точку, в которой прямая пересекает плоскость: 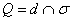 . Хотел разобрать задачу в общем виде, но передумал… лучше традиционный практический пример:
. Хотел разобрать задачу в общем виде, но передумал… лучше традиционный практический пример:
Пример 3
Дана прямая  и плоскость
и плоскость 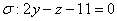 . Требуется:
. Требуется:
а) доказать, что прямая пересекает плоскость;
б) найти точку пересечения прямой и плоскости;
в) через прямую 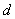 провести плоскость
провести плоскость 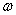 («омега»), перпендикулярную плоскости
(«омега»), перпендикулярную плоскости 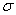 ;
;
г) найти проекцию прямой 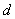 на плоскость
на плоскость 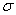 ;
;
д) найти угол между прямой 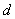 и плоскостью
и плоскостью 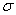 .
.
НеслАбо. А ведь всё началось с единственной точки пересечения =)
Решение: Сначала закрепим задачу о взаимном расположении прямой и плоскости:
а) Из уравнений прямой находим принадлежащую ей точку и направляющий вектор:
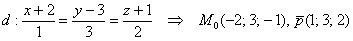
Вектор нормали плоскости, как всегда, сдаётся без боя:

Вычислим скалярное произведение:
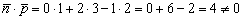 , значит, прямая пересекает плоскость, что и требовалось доказать.
, значит, прямая пересекает плоскость, что и требовалось доказать.
Дата добавления: 2020-11-23; просмотров: 210; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
