Школьная олимпиада по математике
Второй (муниципальный) этап всероссийской олимпиады школьников
по математике 2010/2011 учебный год.
Класс.
1. Рядовой Степанов почистил ведро картошки за 4 часа, однако у него 20% всей картошки ушло в очистки. За сколько часов он наполнит такое же ведро чищеной картошки? (3 балла)
2. Семья ночью подошла к мосту. Папа может перейти его за 1 минуту, мама за 2, сын за 5, бабушка за 10. У них один фонарик. Мост выдерживает только двоих. Как им перейти мост за 17 минут? (Если по мосту идут двое, то они идут с меньшей из их скоростей. Идти по мосту без фонарика нельзя. (Светить издали нельзя, перебрасывать фонарик через реку тоже нельзя). (4 балла)
3. Решите уравнение: |x - 2005| +|2005 - x | =2006. (4 балла)
4. Сколько среди натуральных чисел от 1 до 1983 таких, которые:
а) делятся на 7 и на 9;
б) делятся на 9, но не делятся на 7? (4балла)
5. Один из углов треугольника на 1200 больше другого. Докажите, что биссектриса треугольника, проведенная из вершины третьего угла, вдвое длиннее, чем высота, проведенная из той же вершины? (5 баллов)
Второй (муниципальный) этап всероссийской олимпиады школьников
по математике 2009/2010 учебный год.
Класс.
1. Найдите наименьше число, которое делится на 77, а при делении на 74 дает в остатке 48. (4 балла)
2. Отец с двумя сыновьями отправились навестить бабушку, которая живёт в 33км от города. У отца есть мотороллер, скорость которого 25км/ч, а с пассажиром - 20 км/ч (двух пассажиров на мотороллере перевозить нельзя). Каждый из братьев идёт по дороге со скоростью 5 км/ч. Как им надо действовать, чтобы через три часа всей компанией оказаться у бабушки? (6 баллов)
|
|
|
3. Один сплав состоит из двух металлов, входящих в него в отношении 1:2, а другой сплав содержит те же элементы в отношении 2:3. Из скольких частей обоих сплавов можно получить новый сплав, содержащий те же металлы в отношении 17:27? (4 балла)
4. Пусть в треугольнике АВС выполняется неравенство АС больше ВС. Докажите, что если CD - медиана треугольника АВС, то выполняется условие: угол ACD меньше угла BCD. (5 баллов)
5. На огороженном квадратном поле, сторона которого равна 1км, были построены заборы, разделившие его на прямоугольные участки, размеры которых 5м на 20м и 6м на 12м. Какова общая длина построенных заборов?
(6 баллов)
Второй (муниципальный) этап всероссийской олимпиады школьников
по математике 2008/2009 учебный год.
Класс.
1. Клетки доски 8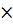 
8 раскрашены в шахматном порядке. Одним ходом разрешается перекрасить любую клетку в цвет одной из соседних с ней клеток. Можно ли с помощью таких перекрашиваний изменить цвет всех клеток на противоположный? (Соседними считаются клетки, имеющие общую сторону)
|
|
|
2. Один сплав состоит из двух металлов, входящих в него в отношении 2:3. Из скольких частей обоих сплавов можно получить новый сплав, содержащий те же металлы в отношении 17:27? (4 баллов)
3. Пусть в треугольнике АВС выполняется неравенство АС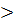 
ВС. Докажите, что для медианы CD треугольника АВС, выполняется условие: угол ACD меньше угла BCD. (5 баллов)
4. Английская задача: Профессор математического факультета Мерль Уайт, профессор философии Лесли Блэк и секретарь деканата Джин Браун завтракали за одним столом.
- Разве не удивительно, - заметила девушка, – что наши фамилии Блэк, Браун и Уайт и что у одного из нас волосы черные, у другого каштановые, а у третьего - совсем белые?
-Действительно, забавно, - заметила особа с чёрными волосами. А вы обратили внимание, что ни у одного из нас цвет волос не соответствует фамилии?
-Точно, вы правы! – воскликнул (или воскликнула) профессор Уайт. Какого цвета волосы у профессора Блэка, если цвет волос у девушек не каштановый?
РS. по - английски «уайт» - белый, «блэк» - черный, «браун» - каштановый.
5. Найдите наименьше число, которое делится на 77, а при делении на 74 дает в остатке 48. (4 балла)
Второй (муниципальный) этап всероссийской олимпиады школьников
|
|
|
по математике 2007/2008 учебный год.
Класс.
1. Найти трехзначное число по следующим данным:
а) число делится на 5;
б) если это число умножить на цифру его единиц, то результат будет больше суммы его цифр на 568. (3 балла)
2. Из двух равных трапеций сложить параллелограммы. Применить результат к выводу формулы площади трапеции. (3 балла)
3. Найти все целые числа х, у, удовлетворяющие уравнению
ху = у + 2х. (4 балла)
4. Доказать, что сумма расстояний всякой точки от вершин многоугольника больше его полупериметра. (4 балла)
5. Доказать, что если число не делится на 7, то его куб, увеличенный или уменьшенный на 1, делится на 7. Установить, в каком случае надо куб числа увеличить, а в каком - уменьшить, чтобы деление нацело было возможным. (5 баллов)
Школьная олимпиада по математике
Дата добавления: 2020-11-23; просмотров: 83; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!