Общие понятия о линейных дифференциальных уравнениях первого порядка.
Прежде, чем рассмотреть понятие линейных дифференциальных уравнений, ознакомимся с понятием однородных дифференциальных уравнений, а для этого рассмотрим суть однородных функций, так как понятие об однородных дифференциальных уравнениях связано с понятием однородных функций.
Функция называєтся однородною п-го порядка, если все ее члени имеют одно и то же измерение. п .
Например, f(x) = 2х² - 3ху +6у² есть однородная функция второго порядка.
Дифференциальное уравнение первого порядка
P(x,y)dx + Q(x,y)dy = 0 (1)
называєтся однородним, если коэффициенты P(x,y) и Q(x,y) при дифференциальных переменных х и у однородные функции одного и того же порядка.
Причем, выполнив подстановку u=y/x, где u – новая неизвестная функция, однородное дифференциальное уравнение сводится к дифференциальному уравнению с разделяющимися переменными.
Линейным дифференциальным уравнением первого порядка называєтся уравнение вида
y’+ p(x)y = f(x) (2)
где p(x), f(x) – заданные и неперерывные на некотором интервале функции.
Термин «линейное уравнение» объясняется тем, что неизвестная функция и ее производная входят в уравнение в первой степени, то есть линейно.
Решение линейных дифференциальных уравнений первого порядка.
Существуют разные методы интегрирования уравнения (2). Один из них
метод Бернулли заключается в том, что решение этого уравнения ищут в виде произведения
|
|
|
y = uv (3)
где u=u(x), v = v(x) – неизвестные функции от переменной х , причем одна из этих функций произвольная, но не тождественно равная нулю.
Найдя производную y’ = u’v+v’u и подставив значения у и у’ в уравнение (2), получим
u’v+u (v’+p(x)v)= f(x)
воспользовавшись произвольностью в выборе функции v(x), выберем ее так, чтобы
v’+p(x)v = 0 (4)
тогда u’v = f(x) (5)
Решим эти уравнения , разделив в уравнении (4) переменные и проинтегрировав:
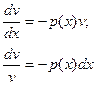
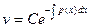- общее решение уравнения (4)
Возьмем за v какое-нибудь частное решение уравнения (4), например при С=1. Подставив его в уравнение (5), находим функцию u
; 
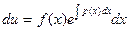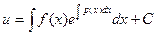(6)
Подставив функции (4) и (6) в произведение (3), получим общее решение уравнения (2)
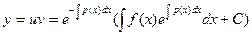(7)
6. Дифференциальные уравнения второго порядка.
План.
1. Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами.
2. Примеры решения дифференциальных уравнений второго порядка.
3. Решение дифференциальных уравнений в комплексных числах.
Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами.
Напомним, что термин «линейное уравнение» означает то, что уравнение содержит неизвестную функцию и все ее производные только в первой степени.
|
|
|
Линейным дифференциальным уравнением второго порядка называется уравнение первой степени относительно неизвестной функции и ее производных. Будем записывать его так:
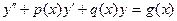(1)
Функции: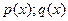 
- называются коэффициентами данного уравнения, а функция
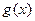- его свободным членом. Если в уравнении (1) его правая часть (свободный член ) равна нулю, то дифференциальное уравнение называется однородным:
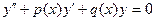(2)
Установим некоторые свойства решений линейного однородного дифференциального уравнения.
Очевидно, что одним из решений уравнения (2) есть : у ≡ 0. Это решение называют нулевым или тривиальным. В дальнейшем, под задачей решения однородного дифференциального уравнения будем понимать задачу отыскания его нетривиальных решений.
Если функции 
- решения уравнения (2), то решением этого уравнения есть также функция:
(3)
Рассмотрим линейное однородное дифференциальное уравнение второго порядка с постоянными коэффициентами
(4)
где p,q – действительные числа..
Эйлер предложил искать частные решения этого уравнения в виде
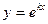(5)
где k – постоянная, которую нужно найти.
|
|
|
Подставив функцию (5) в уравнение (4), получим
,
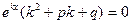Поскольку 
, то
(6)
Квадратное уравнение (6) называется характеристическим уравнением дифференциального уравнения (4). Обозначим корни характеристичного уравнения через 
и рассмотрим возможные случаи:
1) Если - действительные и различные числа, то общее решение уравнения находят по формуле:
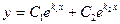(7)
2) Если - действительные и равные числа, то общее решение уравнения находят по формуле:
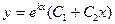(8)
3) Если корни уравнения комплексно-сопряженные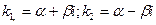 
, то
общее решение уравнения находят по формуле:
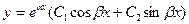(9)
Дата добавления: 2020-11-23; просмотров: 66; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!