Дифференциальные уравнения с разделяющимися переменными.
ЛЕКЦИЯ № 13
Раздел 2. Математический анализ.
Тема: Простейшие дифференциальные уравнения первого и второго порядка.
Цели: сформировать понятие об обыкновенных дифференциальных уравнениях первого и второго порядка, рассмотреть методы решения дифференциальных уравнений, овладеть навыками решения задачи Коши.
План.
1. Общие понятия о дифференциальных уравнениях первого порядка.
2. Задача Коши.
3. Дифференциальные уравнения с разделяющимися переменными.
4. Общие понятия о линейных дифференциальных уравнениях первого порядка.
5. Решение линейных дифференциальных уравнений первого порядка.
6. Дифференциальные уравнения второго порядка
Общие понятия о дифференциальных уравнениях первого порядка.
При изучении интегрального исчисления функции одной переменной появляется необходимость отыскания неизвестной функции по ее производной или дифференциалу.
Уравнение
y ’= f ( x ), или dy = f ( x ) dx (1)
где y - неизвестная функция от х, а f ( x )- заданная функция, является простейшим дифференциальным уравнением. Для его решения, то есть отыскания неизвестной функции у, необходимо проинтегрировать данную функцию f(x). При этом, мы получаем бесконечное множество функций, каждая из которых будет удовлетворять условию (1). Тогда решение уравнения (1) запишется в виде:
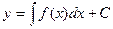
Дифференциальным уравнением первого порядка называется уравнение, которое связывает независимую переменную, неизвестную функцию и ее производную. В общем виде дифференциальное уравнение первого порядка выглядит так:
|
|
|
F ( x , y , y ’)=0 (2)
Если уравнение решено относительно производной, то оно имеет вид:
y ’= f ( x ,у)
и называется уравнением в нормальной форме.
Решением дифференциального уравнения называется функция, которая при подстановке ее вместе с производной в это уравнение, обращает его в верное тождество. Даже простые примеры показывают, что дифференциальные уравнения могут иметь бесконечное множество решений, так как решение содержит произвольную постоянную.
Сделаем вывод:
Любое дифференциальное уравнение (1) имеет бесконечное множество решений. Эту совокупность решений называют общим решением дифференциального уравнения первого порядка:
у =φ(х,С) .
Напомним, что порядком дифференциального уравнения считается порядок старшей производной, входящей в уравнение.
Рассмотрим решение дифференциальных уравнений на примере задач:
1) Найдите уравнение кривой, если угловой коэффициент касательной в каждой точке этой кривой равен ординате этой точки.
Решение: Согласно геометрического смысла производной,
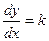, а по условию k = y , составим дифференциальное уравнение: 
,
|
|
|
Решением уравнения будет функция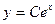 
.
2) Найдите закон движения тела, если оно двигается со скоростью v = 4t – 6t².
Известно, что при прямолинейном движении скорость является производной от пути по времени, обозначим путь через х , имеем
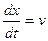, тогда 
, проинтегрировав обе части уравнения, получим закон движения: X=2t² -2t³ +C.
Задача Коши.
Рассмотрим теорему Коши, которая дает достаточные условия существования единственного решения дифференциального уравнения.
Теорема:
Пусть функция y = f ( x ,у) и ее частная производная по переменной у
y ’= f ( x ,у)
определены и непрерывны в открытой области G плоскости Оху и точка 
Є G. Тогда существует единственное решение у =φ(х) дифференциального уравнения, которое удовлетворяет условию:
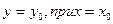(3)
Условие (3), согласно которого решение принимает наперед заданные значения в заданной точке, называют начальными условиями и записывают так:
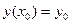
Задача нахождения решения дифференциального уравнения, которое удовлетворяет начальному условию (4), называется задачей Коши.
С точки зрения геометрии, решить задачу Коши – это значит выделить из множества интегральных кривых ту, которая проходит через заданную точку.
|
|
|
Всякое решение, которое получено из общего решения, если дать определенные значения произвольным постоянным, называется частным решением этого дифференциального уравнения.
Рассмотрим пример решения задачи Коши.
1) Найти решение дифференциального уравнения 3y²dy = (4x³+5)dx, которое удовлетворяет начальному условию: у = 2, при х = 1.
Решение.
Найдем общее решение данного уравнения: 
,
Используя начальные условия, найдем неизвестную постоянную, которая им удовлетворяет: 8 = 1+5+С, С= 2.
Запишем частное решение дифференциального уравнения:
.
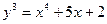Задача Коши решена.
Дифференциальные уравнения с разделяющимися переменными.
Дифференциальные уравнения вида
f( x ) dy = g ( y ) dx
нельзя сразу решить интегрированием, так как левая и правая его части имеют две независимые переменные, а для интегрирования необходимо, чтобы каждая переменная находилась в той части уравнения, в которой находится ее диференциал.
Дифференциальные уравнения, в которых переменные можно разделить, если умножить обе части уравнения на одно и то же выражение, называются дифференциальными уравнениями с разделяющимися переменными.
Нужно помнить, что при делении обеих частей уравнения на функцию, можно потерять некоторые решения.
|
|
|
Чаще всего общее решение дифференциального уравнения получаем в неявном виде и нет особой нужды решать его относительно одной из переменных, так как в дифференциальном уравнении независимые переменные считаются равноправными.
Например: решить дифференциальное уравнение:
,
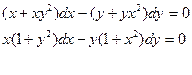Разделим переменные и получим
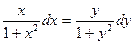, проинтегрировав обе части, получим:
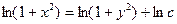, пропотенцировав, получим общее решение данного дифференциального уравнения:
.
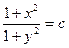Дата добавления: 2020-11-23; просмотров: 68; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!