Нахождение производных сложных функций
Производные элементарных функций
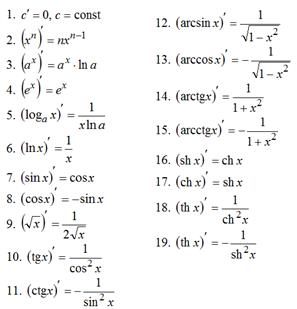
| Основные правила дифференцирования

|
| | |
Пример 1:
Найти производную функции:
а) 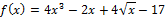
Вычисляем по правилу производной суммы (разность):
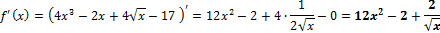
Ответ: 
б) 
Вычисляем по правилу производной произведения:

Ответ: 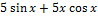
в) 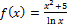
Вычисляем по правилу производной частного:
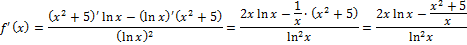
Это выражение можно преобразовать, тогда получим:

Ответ: 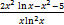
г)  10x
10x
Вычисляем по правилу производной сложной функции, где arcctg □ - внешняя функция, а 10x – внутренняя:
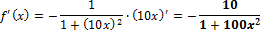
Ответ: 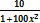
д) 
Вычисляем по правилу производной сложной функции. Здесь несколько функций, от каждой находим производную:
 ln □
ln □ 

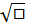
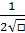
 cos□ -sin□
cos□ -sin□
 3x 3
3x 3
Получаем:
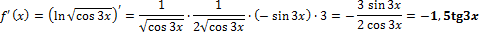
Ответ: 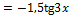
Пример 2
Составим уравнение касательной и нормали к графику функции  в точке с абсциссой
в точке с абсциссой
x0 = -2.
Выполняем по алгоритму:
1) f (x0) = 2 · (-2)3 – (-2) + 5 = 2 · (-8) + 2 + 5 = -16 + 2 + 5 = −9
2) f ′ (x) = (2x3 – x + 5)′ = 6x2 – 1
3) f ′(x0) = 6 · (-2)2 -1 = 6 · 4 – 1 = 24 – 1 = 23
Уравнение касательной (подставляем):
y = f (x0) + f ′ (x0) · (x – x0)
y = −9 + 23(x + 2)
y = 9 + 23x + 46
y = 23 x + 55
Уравнение нормали (подставляем):
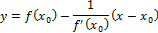
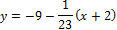
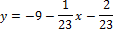
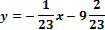
Ответ: y = 23x + 55
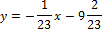
Пример 3
Тело движется прямолинейно по закону 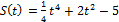 (м)
(м)
Найдите его скорость и ускорение в момент времени t = 2c .
1) 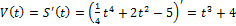
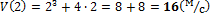
2) 
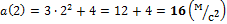
Ответ: 
Пример 4
Тело движется прямолинейно по закону 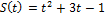 (м)
(м)
Найдите его скорость и ускорение в момент времени t = 5c .
3) 

4) 

Ответ: 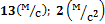
Вычисление неопределенных интегралов методом подстановки и по частям
Таблица интегралов
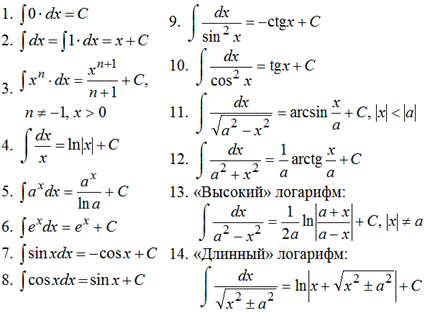
Примеры:
Найти неопределенные интегралы:
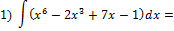
находим первообразную от каждого слагаемого по первой табличной формуле:
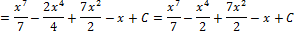
Ответ: 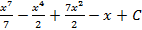
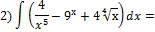
применяя свойства степеней записываем первое и третье слагаемое в виде степени:

к первому и третьему слагаемым применяем первую формулу, ко второму слагаемому третью табличную формулу:

Ответ: 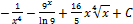
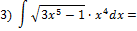
интегрируем подстановкой:
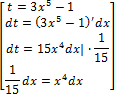
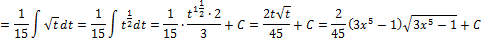
Ответ: 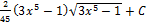
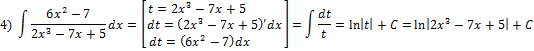
Ответ: 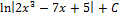

Ответ: 

применяем метод интегрирования по частям
это II тип
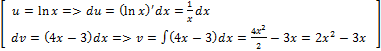 =
=
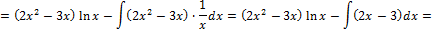
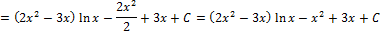
Ответ: 

это интеграл III типа в методе интегрирования по частям:
 ⊜
⊜
отдельно находим последний интеграл и найденное выражение подставим обратно:
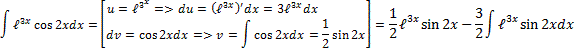
Тогда:

Составим уравнение и находим из него искомый интеграл:
 |
+



Ответ: 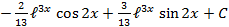
Дата добавления: 2020-11-15; просмотров: 80; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!

