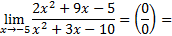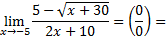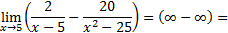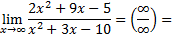Решение систем линейных уравнений по формулам Крамера.
Методические указания по выполнению контрольной работ по математике
Для студентов группы Б-1з
Матрицы
Определение:
Матрицей размера m 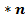 называется прямоугольная таблица чисел, содержащая m строк и
называется прямоугольная таблица чисел, содержащая m строк и 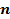 столбцов. Числа, составляющие матрицу, называются элементами матрицы.
столбцов. Числа, составляющие матрицу, называются элементами матрицы.
Матрицы обозначаются: A,B,C,D…
Элементы матрицы: 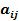 ,где i – номер строки;
,где i – номер строки;
j – номер столбца
Например: 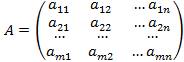
Например, матрица размера 2*3: 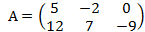
Виды матриц:
ü Матрица, состоящая из одной строки, называется матрицей - строкой, а из одного столбца называется матрицей – столбцом, например:
А= 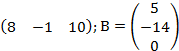
ü Матрица называется квадратной 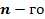 порядка, если число её строк равно числу её столбцов.
порядка, если число её строк равно числу её столбцов.
Например:
А= 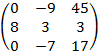 -квадратная матрица 3-го порядка
-квадратная матрица 3-го порядка
ü Элементы матрицы 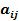 , у которых номер строки равен номеру столбца (i= j), называются диагональными и образуют главную диагональ матрицы. Для квадратной матрицы главную диагональ образуют элементы
, у которых номер строки равен номеру столбца (i= j), называются диагональными и образуют главную диагональ матрицы. Для квадратной матрицы главную диагональ образуют элементы 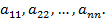
ü Если все недиагональные элементы квадратной матрицы равны нулю, то матрица называется диагональной.
Например:
А= 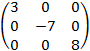 - диагональная матрица 3-го порядка
- диагональная матрица 3-го порядка
ü Если у диагональной матрицы  порядка все диагональные элементы равны единице, то матрица называется единичной матрицей
порядка все диагональные элементы равны единице, то матрица называется единичной матрицей 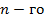 порядка, она обозначается Е.
порядка, она обозначается Е.
Например:
Е= 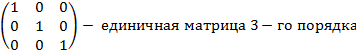
ü Матрица любого размера называется нулевой, или нуль – матрицей, если все её элементы равны нулю.
|
|
|
Например:
О= 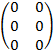
Операции над матрицами:
1) Умножение матрицы на число:
Чтобы умножить матрицу на число, нужно каждый элемент матрицы умножить на это число.
Например :
Пусть дана матрица А= 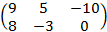 .Найти матрицу В=3А
.Найти матрицу В=3А
Решение: В=3 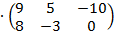 =
= 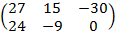
Ответ: В= 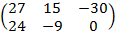
Замечание: произведение матрицы на нуль есть нулевая матрица.
2) Сложение матриц:
Матрицы складываются поэлементно.
Замечание: Слагаемые матрицы должны быть одинакового размера!
Например:
Дано: А= 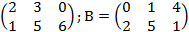
Найти: А+В
Решение: А+В= 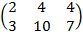
Ответ: 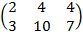
Замечание: А+О=А
3) Вычитание матриц:
Матрицы вычитаются почленно.
Разность двух матриц можно определить через предыдущие операции: А-В=А+(-В)
Пример 1:
Даны две матрицы 
Найдите матрицу С=-4А-2В
Решение:
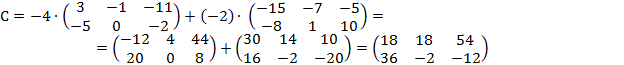
Ответ: 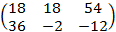
4) Умножение матриц:
Умножение матрицы А на матрицу В определено. когда число столбцов первой матрицы равно числу строк второй матрицы, говорят, матрица А согласованная с матрицей В.
Произведением матриц называется такая матрица, каждый элемент которой равен сумме произведений элементов i – той строки первой матрицы на соответствующие элементы j – го столбца второй матрицы:
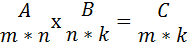
Пример 2:
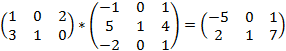
|
|
|
2*3 3*3 2*3
Каждый элемент итоговой матрицы удобней рассчитать отдельно:
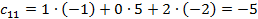
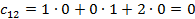
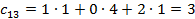
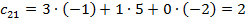
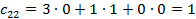
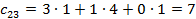
Ответ: 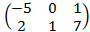
Замечание: Переместительный (коммуникативный) закон умножения матриц, вообще говоря, не выполняется: А 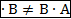
5) Возведение в степень:
Операция возведения в степень выполняется только для квадратных матриц.
Целой положительной степенью 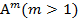 квадратной матрицы А называется произведение m матриц, равных А:
квадратной матрицы А называется произведение m матриц, равных А:
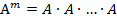
Например:
Найти 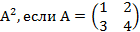
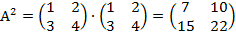
Ответ: 
6) Транспонирование матрицы:
Транспонирование матрицы – это переход от матрицы А к матрице 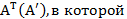 строки и столбцы поменялись местами с сохранением порядка.
строки и столбцы поменялись местами с сохранением порядка.
Пример:
Если дана матрица А= 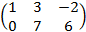 ,то транспонированная матрица
,то транспонированная матрица 
Определитель
Определение:
Определителем матрицы первого порядка называется элемент этой матрицы:
Для матрицы 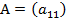 определитель
определитель 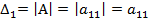
Определителем матрицы второго порядка называется число, которое вычисляется по формуле:



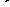
 -
- 
Пример:
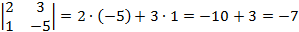
Определитель матрицы третьего порядка вычисляется по правилу Сарруса (правилу треугольников):








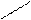


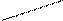



 -
- 
Пример 3:
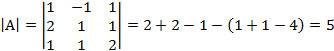
Ответ: 5
Решение систем линейных уравнений по формулам Крамера.
|
|
|
Алгоритм решения:
1) Находим главный определитель системы: 
2) Находим определители при неизвестных, т. е. вспомогательные определители: 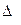 , полученные из главного определителя заменой j- ого столбца столбцом свободных членов.
, полученные из главного определителя заменой j- ого столбца столбцом свободных членов.
3) Находим 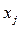 по формулам Крамера:
по формулам Крамера: 
4) Записываем ответ.
Возможны случаи:
1) Если  , то система уравнения имеет единственное решение.
, то система уравнения имеет единственное решение.
2) Если 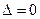 и каждый
и каждый 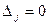 , то система имеет бесконечное множество решений.
, то система имеет бесконечное множество решений.
3) Если 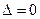 и хотя бы один из определителей
и хотя бы один из определителей 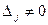 , то система решений не имеет.
, то система решений не имеет.
Пример 1:Решить систему уравнений методом Крамера: 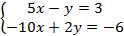
Решение:
1) Находим главный определитель системы: 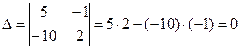
2) Находим определители при неизвестных, т. е. вспомогательные определители: 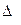 , полученные из главного определителя заменой j- ого столбца столбцом свободных членов.
, полученные из главного определителя заменой j- ого столбца столбцом свободных членов.
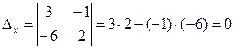
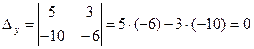
3)  , значит, система имеет бесконечное множество решений.
, значит, система имеет бесконечное множество решений.
Ответ: система имеет бесконечное множество решений
Пример 2:Решить систему уравнений методом Крамера: 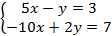
Решение:
1) Находим главный определитель системы: 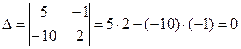
2) Находим определители при неизвестных, т. е. вспомогательные определители: 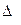 , полученные из главного определителя заменой j- ого столбца столбцом свободных членов.
, полученные из главного определителя заменой j- ого столбца столбцом свободных членов.
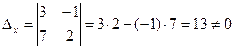
3) 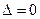 и хотя бы один из определителей
и хотя бы один из определителей 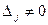 , то система решений не имеет.
, то система решений не имеет.
|
|
|
Ответ: система решений не имеет
Пример 3:Решить систему уравнений методом Крамера: 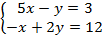
Решение:
1) Находим главный определитель системы: 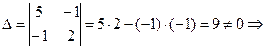 система имеет единственное решение
система имеет единственное решение
2) Находим определители при неизвестных, т. е. вспомогательные определители: 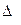 , полученные из главного определителя заменой j- ого столбца столбцом свободных членов.
, полученные из главного определителя заменой j- ого столбца столбцом свободных членов.

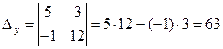
3) Находим 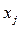 по формулам Крамера:
по формулам Крамера: 
Ответ: (2;7)
Пример 4:Решить систему уравнений методом Крамера: 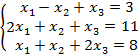
Решение:
I. Находим главный определитель системы:
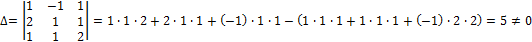 =>система имеет единственное решение
=>система имеет единственное решение
II. Находим определители при неизвестных, т. е. вспомогательные определители: 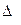 , полученные из главного определителя заменой j- ого столбца столбцом свободных членов.
, полученные из главного определителя заменой j- ого столбца столбцом свободных членов.
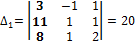 ,
,  ,
, 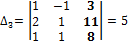
III. Находим  по формулам Крамера:
по формулам Крамера:

Ответ: (4;2;1)
3. Пределы функции в точке и на бесконечности
1 Предел функции в точке
|
1)
Числитель и знаменатель дроби раскладывается на множители по формуле разности квадратов:
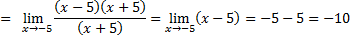
Ответ: −10
|
2)
 Числитель и знаменатель дроби раскладывается на множители по формуле
Числитель и знаменатель дроби раскладывается на множители по формуле 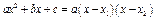 :
:
 |
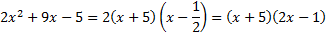
D = 81 – 4 · 2 · (−5) = 81 + 40 = 121
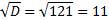
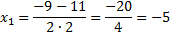
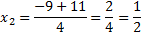
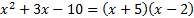
D = 9 – 4 · 1 · (−10) = 9 + 40 = 49
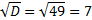
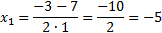
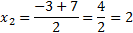
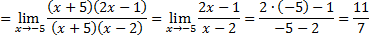
Ответ: 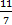
|
3)
Числитель и знаменатель дроби умножаем на выражение, сопряженное выражению с корнями (правило 2):
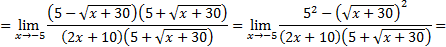
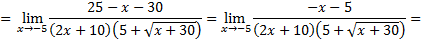

Ответ: 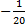
|
4)
Приводим дроби к наименьшему общему знаменателю:
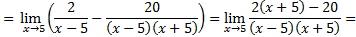

Числитель и знаменатель раскладываем на множители (правило 1):
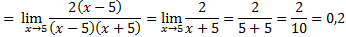
Ответ: 0,2
2 Предел функции на бесконечность
|
1)
Каждое слагаемое числителя и знаменателя дроби делим на x2 (правило 3):
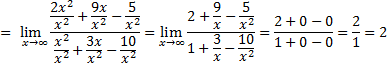
Ответ: 2
|
2)
Числитель и знаменатель дроби умножаем на выражение, сопряженное выражению с корнями (правило 2):
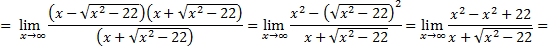
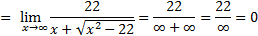
Ответ: 0
3. Замечательные пределы
|
1)
Применяем I замечательный предел, умножаем числитель и знаменатель дроби на 5:
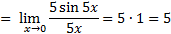
Ответ: 5
|
2)
Применяем I замечательный предел, умножаем числитель и знаменатель дроби на 5:
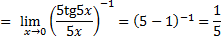
Ответ: 
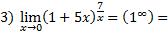
Применяем II замечательный предел:
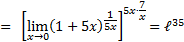
Ответ: 
|
4)
Ответ: 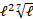
Дата добавления: 2020-11-15; просмотров: 54; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!