Трехмерные матричные преобразования

⇐ ПредыдущаяСтр 3 из 5Следующая ⇒

В однородной системе координат трехмерные преобразования могут быть представлены матрицами размером . Тогда трехмерная точка 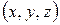записывается в однородных координатах как , где . Для получения декартовых координат надо первые три однородные координаты разделить на . Два однородных вектора описывают одну декартову точку в трехмерном пространстве, если 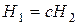, где и - векторы, записанные в однородных координатах. В нашем случае просто .

Матрицы преобразований будем записывать в правосторонней системе координат. При этом положительный поворот определяется следующим образом. Если смотреть из положительной части оси вращения (например, оси ) в направлении начала координат, то поворот на 90° против часовой стрелки будет переводить одну положительную полуось в другую (ось в 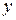, в соответствии с правилом циклической перестановки).

Заметим, что на практике удобнее применять левостороннюю систему координат, т. к. в этом случае удобнее интерпретировать тот факт, что точки с большими значениями находятся дальше от наблюдателя.

Запишем теперь матрицу трехмерного переноса. Аналогично двумерному случаю: 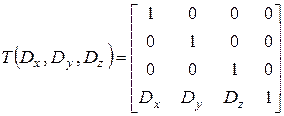, при этом

Операция масштабирования:

Перейдем к операции поворота, с ней в трехмерном случае придется разбираться побольше, чем в двумерном. Так как при двумерном повороте в плоскости 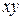координаты остаются неизменными, то поворот вокруг оси записывается так: .

Матрица поворота вокруг оси имеет вид:

и вокруг оси (обратите внимание на смену положения синуса угла с отрицательным знаком): .

Обратные преобразования (т.е. приводящие к противоположным действиям) будут выражаться обратными матрицами. Для операции переноса надо лишь заменить знаки компонент вектора переноса на противоположные:

;

для операции масштабирования – на обратные значения:

;

для поворота – выбором отрицательного угла поворота:

;

не забываем, что cos(-a)=cos(a), а sin(-a)=-sin(a).

Результатом нескольких последовательных поворотов будет матрица

Здесь верхняя матрица размером (В) называется ортогональной. Важным ее свойством является то, что обратная к ней матрица является транспонированной: . Это полезно тем, что при вычислениях достаточно поменять индексы местами и обратное преобразование получается автоматически.

После перемножения любого числа матриц вида и результирующая матрица всегда будет иметь вид

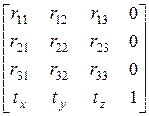Здесь верхняя часть размером определяет суммарный поворот и масштабирование, а три коэффициента последней строки – суммарный перенос. Правая подматрица 3х1 отвечает за проецирование (как правило, не нулевым является лишь один элемент) на соответствующую плоскость.

Таким образом, с помощью композиции матричных преобразований можно получить одно общее результирующее преобразование. Для этого будем использовать матрицы T, S и R. С вычислительной точки зрения гораздо проще и быстрее применять матрицу уже готового результирующего преобразования к точке вместо того, чтобы применять их последовательно одну за другой.

Для примера рассмотрим задачу поворота объекта на плоскости относительно некоторой произвольной точки . Пока мы умеем поворачивать объекты только вокруг начала координат. Но можно представить эту задачу как последовательность шагов, на каждом из которых будет применяться только элементарная операция: перенос, масштабирование или вращение.

Вот эта последовательность элементарных преобразований (рис. 5):

1. Перенос, при котором точка переходит в начало координат.

2. Поворот на заданный угол.

3. Перенос, при котором точка из начала координат возвращается в первоначальное положение .

Рис. 5. Последовательность преобразований при повороте объекта
вокруг точки 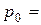на угол a

Точка 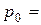. Первый перенос производится на вектор Т , поворот на R(a), а обратный перенос ‑ на вектор Т (Т^-1).

Дата добавления: 2020-11-15; просмотров: 149; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 1 234 5 Следующая ⇒

Мы поможем в написании ваших работ!