Задание многоугольников с помощью указателей.
При использовании этого представления каждый узел полигональной сетки запоминается лишь один раз в списке вершин. Многоугольник определяется списком указателей (или индексов) в списке вершин.
Список многоугольников:
Достоинства:
1. Вершины входят в описание 1 раз.
2. можно легко изменять вершины.
Недостаток: При выводе на экран каждое ребро может прорисоваться несколько раз.
3. Задание многоугольников с помощью ребер.
Есть список вершин P и список ребер E.
Теперь многоугольник рассматривается как совокупность указателей на элементы списка ребер, в котором ребра встречаются лишь один раз. Каждое ребро в списке ребер указывает на две вершины в списке вершин, определяющие это ребро.
Способы задания многоугольников.
Представление объекта в виде каркаса.
1. Список, матрица вершин P ‑ единичный куб от (0,0,0) вправо-назад, низ против часовой 1234, верх – 6785
2. Список ребер E. Ребро – отрезок прямой, определяется двумя вершинами.
Каркас объекта – это совокупность вершин и ребер объекта. Вершины образуют список или матрицу вершин, ребра – матрицу ребер.
Геометрические преобразования объекта.
Смоделированный объект можно перемещать в пространстве, вращать и изменять в размерах. При этом изменяются только координаты вершин (список вершин), список ребер – неизменен.
Три вида изменения:
1. Перенос. T(Rx, Ry, Rz)
|
|
|
Если применить перенос не для всех вершин, то объект деформируется.
2. Масштабирование. M(Sx,Sy,Sz)
Если объект задан не в начале координат, то при Sx, Sy, Sz > 1 объект удалится, а при Sx, Sy, Sz <1 – приблизится.
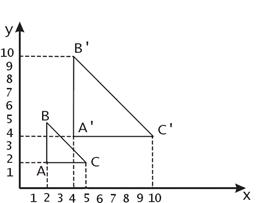
3. Поворот. Rx(α), Ry(α), Rz(α) – относительно. осей
Осуществляется относительно начала координат А->В.
A: 
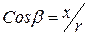
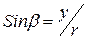
Формулы задают вращение вокруг осей координат. Поворот вокруг произвольной оси можно свести к переносу и повороту вокруг оси координат.
Однородные координаты
Два преобразования точек на плоскости из трех – операции вращения и масштабирования ‑ описываются в виде произведения матрицы на вектор, а третья – операция переноса – описывается как сумма двух векторов. В случае последовательного выполнения любой комбинации операций вращения и масштабирования результат легко можно записать в виде произведения матриц соответствующих преобразований. Это будет матрица результирующего поворота и масштабирования. Очевидно, что удобнее применять результирующую матрицу вместо того, чтобы каждый раз заново вычислять произведение матриц. Однако таким способом нельзя получить эту результирующую матрицу преобразования, если среди последовательности преобразований присутствует хотя бы один перенос. Матричное произведение в компьютерной графике также называют композицией. Было бы удобнее иметь математический аппарат, позволяющий включать в композиции преобразований все три выше указанные операции. При этом получился бы значительный выигрыш в скорости вычислений. Однородные координаты и есть этот математический аппарат.
|
|
|
Двумерный вектор 
в однородных координатах записывается в виде 
, где 
. Число 
называется масштабным множителем. Для того чтобы из вектора, записанного в однородных координатах, получить вектор в обычных координатах, необходимо разделить первые две координаты на третью: 
.
В общем случае осуществляется переход от n-мерного пространства к
-мерному. Это преобразование не единственное. Обратное преобразование называется проекцией однородных координат.
Дата добавления: 2020-11-15; просмотров: 188; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!