Смешанное произведение и его свойства.
Темы вопросов
1. Вектор. Основные понятия. Линейные операции. 2
2. Проекция вектора на ось. Разложение вектора по ортам координатных осей. Действия над векторами, заданными проекциями. 4
3. Скалярное произведение векторов и его свойства. 5
4. Векторное произведение и его свойства. 7
5. Смешанное произведение и его свойства. 8
6. Матрицы. Основные понятия. Сложение и разность матриц. 10
7. Матрицы. Основные понятия. Умножение на число и произведение. Элементарные преобразования матриц. 12
8. Определители. Правила вычисления. Ранг матрицы. Свойства ранга. 15
9. Свойства определителей. 19
10. Система линейных алгебраических уравнений. Основная и расширенная матрица. Совместная, несовместная и однородная системы уравнений. 21
1. Вектор. Основные понятия. Линейные операции.
При изучении различных разделов физики, механики и технических наук встречаются величины, которые полностью определяются заданием их числовых значений. Такие величины называются скалярными или, короче, скалярами. Скалярными величинами, например, являются длина, площадь, объем, масса, температура тела и др.
Помимо скалярных величин, в различных задачах встречаются величины, для определения которых, кроме числового значения, необходимо знать также их направление. Такие величины называются векторными. Физическими примерами векторных величин могут служить смещение материальной точки, двигающейся в пространстве, скорость и ускорение этой точки, а также действующая на нее сила.
Векторные величины изображаются с помощью векторов.
Вектором называется направленный отрезок, имеющий определенную длину, т.е. отрезок определенной длины, у которого одна из ограничивающих его точек принимается за начало, а вторая – за конец. Если А – начало вектора и В – его конец, то вектор обозначается символом 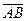 . Вектор можно обозначать и одной малой латинской буквой с чертой над ней, например, . Вектор можно обозначать и одной малой латинской буквой с чертой над ней, например,  . Изображается вектор отрезком со стрелкой на конце. Начало вектора называют точкой его приложения. Если точка А является началом вектора . Изображается вектор отрезком со стрелкой на конце. Начало вектора называют точкой его приложения. Если точка А является началом вектора  , то мы будем говорить, что вектор приложен в точке А.
Длина вектора , то мы будем говорить, что вектор приложен в точке А.
Длина вектора 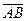 называется его модулем и обозначается символом | называется его модулем и обозначается символом | 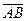 |. Модуль вектора |. Модуль вектора  обозначается | обозначается |  |.
Вектор |.
Вектор  , для которого | , для которого |  | = 1, называется единичным. Обозначается | = 1, называется единичным. Обозначается 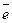 .
Единичный вектор, направление которого совпадает с направлением вектора .
Единичный вектор, направление которого совпадает с направлением вектора  , называется ортом вектора , называется ортом вектора  .
Вектор, длина которого равна 0, называется нулевым. Нулевой вектор не имеет определенного направления, а начало и конец его совпадают. Обозначается .
Вектор, длина которого равна 0, называется нулевым. Нулевой вектор не имеет определенного направления, а начало и конец его совпадают. Обозначается 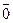 . Векторы . Векторы  и и  , расположенные на одной прямой или на параллельных прямых, называются коллинеарными. Они могут быть одинаково или противоположно направлены.
Два векторы , расположенные на одной прямой или на параллельных прямых, называются коллинеарными. Они могут быть одинаково или противоположно направлены.
Два векторы  и и  называются равными, если они коллинеарны, имеют одинаковую длину и одинаковое направление.
В этом случае пишут: называются равными, если они коллинеарны, имеют одинаковую длину и одинаковое направление.
В этом случае пишут:  = =  . Все нулевые векторы считаются равными. Из определения равенства векторов следует, что вектор можно переносить, помещая его начало в любую точку пространства. Такой вектор называется свободным.
Три вектора в пространстве называются компланарными, если они лежат в одной плоскости или в параллельных плоскостях. Если среди трех векторов хотя бы один нулевой, или два любые коллинеарны, то эти вектора также компланарны.
Два коллинеарных вектора (отличные от нулевых векторов), имеющие равные модули, но противоположно направленные, называются противоположными. Вектор, противоположный вектору . Все нулевые векторы считаются равными. Из определения равенства векторов следует, что вектор можно переносить, помещая его начало в любую точку пространства. Такой вектор называется свободным.
Три вектора в пространстве называются компланарными, если они лежат в одной плоскости или в параллельных плоскостях. Если среди трех векторов хотя бы один нулевой, или два любые коллинеарны, то эти вектора также компланарны.
Два коллинеарных вектора (отличные от нулевых векторов), имеющие равные модули, но противоположно направленные, называются противоположными. Вектор, противоположный вектору  , обозначается – , обозначается –  . Для вектора . Для вектора 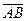 противоположным будет вектор противоположным будет вектор  .
Линейные операции над векторами. Линейными операциями называются операции сложения и вычитания векторов и умножения вектора на число. .
Линейные операции над векторами. Линейными операциями называются операции сложения и вычитания векторов и умножения вектора на число.
| 2. Проекция вектора на ось. Разложение вектора по ортам координатных осей. Действия над векторами, заданными проекциями.
Определение 1. Углом между векторами  и и  называется наименьший угол называется наименьший угол 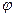 ( ( 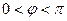 ), на который надо повернуть один из векторов до его совпадения со вторым после приведения этих векторов к общему началу.
Осью называется направленная прямая. Направление прямой на рисунке обычно обозначается стрелкой. Заданное направление оси считается положительным, противоположное – отрицательным.
Рассмотрим ось l , положительное направление которой совпадает с направлением единичного вектора ), на который надо повернуть один из векторов до его совпадения со вторым после приведения этих векторов к общему началу.
Осью называется направленная прямая. Направление прямой на рисунке обычно обозначается стрелкой. Заданное направление оси считается положительным, противоположное – отрицательным.
Рассмотрим ось l , положительное направление которой совпадает с направлением единичного вектора 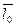 , расположенного на оси l. Такой вектор называется ортом оси l.
Определение 2. Углом между вектором , расположенного на оси l. Такой вектор называется ортом оси l.
Определение 2. Углом между вектором  и осью l называется угол и осью l называется угол 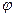 между векторами между векторами  и и 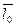 .
Определение 3. Проекцией точки А на ось l называется точка .
Определение 3. Проекцией точки А на ось l называется точка 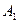 , в которой пересекается ось l с плоскостью, перпендикулярной к l, проходящей через точку А.
Определение 4. Компонентой (составляющей) вектора , в которой пересекается ось l с плоскостью, перпендикулярной к l, проходящей через точку А.
Определение 4. Компонентой (составляющей) вектора  на ось l называется вектор на ось l называется вектор 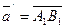 , где , где 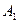 , , 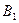 соответственно проекции точек A , B на l.
Определение 5. Проекцией вектора соответственно проекции точек A , B на l.
Определение 5. Проекцией вектора  на ось l ( на ось l (  ) называется длина его компоненты ) называется длина его компоненты  на ось l, взятая со знаком «плюс», если направление компоненты совпадает с направлением оси l, и со знаком «минус», если направление компоненты противоположно направлению оси l.
Если на ось l, взятая со знаком «плюс», если направление компоненты совпадает с направлением оси l, и со знаком «минус», если направление компоненты противоположно направлению оси l.
Если  = 0, то полагают = 0, то полагают  = 0.
Теорема 1. Проекция вектора = 0.
Теорема 1. Проекция вектора  на ось l равна произведению его модуля на косинус угла на ось l равна произведению его модуля на косинус угла 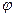 между этим вектором и осью l : между этим вектором и осью l :
| 3. Скалярное произведение векторов и его свойства.
Определение. Скалярным произведением двух векторов называется число, равное произведению модулей этих векторов на косинус угла между ними.
Скалярное произведение векторов  и и  обозначается символом обозначается символом 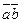 или ( или (  , ,  ). Если угол между векторами ). Если угол между векторами  и и  равен равен 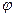 , то , то
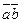 = = 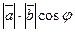 .
Через .
Через 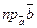 обозначим проекцию вектора обозначим проекцию вектора  на ось с направлением вектора на ось с направлением вектора  . Так как . Так как 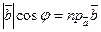 и и 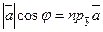 , можно записать , можно записать
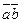 = = 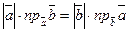 ,
т.е. скалярное произведение двух векторов равно модулю одного из них, умноженному на проекцию другого на ось с направлением первого.
Раскроем физический смысл скалярного произведения. Если вектор ,
т.е. скалярное произведение двух векторов равно модулю одного из них, умноженному на проекцию другого на ось с направлением первого.
Раскроем физический смысл скалярного произведения. Если вектор  изображает силу, точка приложения которой перемещается из начала в конец вектора изображает силу, точка приложения которой перемещается из начала в конец вектора  , то работа A указанной силы определяется равенством , то работа A указанной силы определяется равенством
 ,
т.е. равна скалярному произведению векторов ,
т.е. равна скалярному произведению векторов  и и  .
Свойства:
1. .
Свойства:
1.  (переместительное свойство);
2. (переместительное свойство);
2. 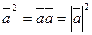 (
(  называется скалярным квадратом вектора);
3. называется скалярным квадратом вектора);
3. 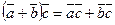 (распределительное свойство);
4. (распределительное свойство);
4.  (сочетательное свойство относительно числового множителя). (сочетательное свойство относительно числового множителя).
| 4. Векторное произведение и его свойства.
Определение. Векторным произведением двух векторов  и и  называется новый вектор называется новый вектор 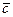 , модуль которого равен площади параллелограмма, построенного на векторах , модуль которого равен площади параллелограмма, построенного на векторах  и и  , приведенных к общему началу, и который перпендикулярен к перемножаемым векторам (иначе говоря, перпендикулярен к плоскости построенного на них параллелограмма) и направлен в такую строну, чтобы кратчайший поворот от , приведенных к общему началу, и который перпендикулярен к перемножаемым векторам (иначе говоря, перпендикулярен к плоскости построенного на них параллелограмма) и направлен в такую строну, чтобы кратчайший поворот от  к к  вокруг полученного вектора вокруг полученного вектора 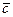 представлялся происходящим против часовой стрелки, если смотреть из конца вектора представлялся происходящим против часовой стрелки, если смотреть из конца вектора 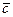 Свойства векторного произведения:
1. При перестановке сомножителей векторное произведение меняет знак, т.е.
Свойства векторного произведения:
1. При перестановке сомножителей векторное произведение меняет знак, т.е.
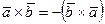 .
Это свойство следует из определения векторного произведения.
Таким образом, векторное произведение не обладает переместительным свойством.
2. .
Это свойство следует из определения векторного произведения.
Таким образом, векторное произведение не обладает переместительным свойством.
2. 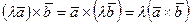 ,
где ,
где 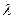 – скаляр.
Свойство 2 непосредственно вытекает из смысла произведения вектора на скаляр и определения векторного произведения.
3. Векторное произведение подчиняется распределительному закону, т.е. – скаляр.
Свойство 2 непосредственно вытекает из смысла произведения вектора на скаляр и определения векторного произведения.
3. Векторное произведение подчиняется распределительному закону, т.е.
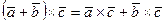 .
4. Если векторное произведение двух векторов равно нулевому вектору, то либо равен нулевому вектору хотя бы один из перемножаемых векторов (тривиальный случай), либо равен нулю синус угла между ними, т.е. векторы коллинеарны.
Обратно, если два ненулевых вектора коллинеарны, то их векторное произведение равно нулевому вектору. Таким образом, для того чтобы два ненулевых вектора .
4. Если векторное произведение двух векторов равно нулевому вектору, то либо равен нулевому вектору хотя бы один из перемножаемых векторов (тривиальный случай), либо равен нулю синус угла между ними, т.е. векторы коллинеарны.
Обратно, если два ненулевых вектора коллинеарны, то их векторное произведение равно нулевому вектору. Таким образом, для того чтобы два ненулевых вектора  и и  были коллинеарны, необходимо и достаточно, чтобы их векторное произведение равнялось нулевому вектору. Отсюда, в частности, следует, что векторное произведение вектора на самого себя равно нулевому вектору. были коллинеарны, необходимо и достаточно, чтобы их векторное произведение равнялось нулевому вектору. Отсюда, в частности, следует, что векторное произведение вектора на самого себя равно нулевому вектору.
|
|
|
|
|
|
|
|
|
|
|
|
|
Смешанное произведение и его свойства.
Пусть даны три вектора  ,
,  и
и 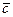 . Представим себе, что вектор
. Представим себе, что вектор  умножается векторно на
умножается векторно на  и полученный вектор
и полученный вектор 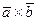 умножается скалярно на вектор
умножается скалярно на вектор 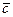 , тем самым определяется число
, тем самым определяется число 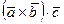 . Оно называется векторно-скалярным или смешанным произведением трех
. Оно называется векторно-скалярным или смешанным произведением трех  ,
,  и
и 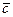 . Для краткости смешанное произведение
. Для краткости смешанное произведение 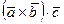 будем обозначать
будем обозначать 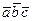 или (
или ( 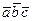 ).
).
Выясним геометрический смысл смешанного произведения 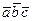 . Пусть рассматриваемые векторы
. Пусть рассматриваемые векторы  ,
,  и
и 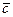 некомпланарны. Построим параллелепипед на векторах
некомпланарны. Построим параллелепипед на векторах  ,
,  и
и 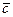 как на ребрах. Векторное произведение
как на ребрах. Векторное произведение 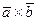 есть вектор
есть вектор 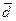
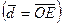 , численно равный площади параллелограмма OADB (основание построенного параллелепипеда), построенного на векторах
, численно равный площади параллелограмма OADB (основание построенного параллелепипеда), построенного на векторах  и
и  , и направленный перпендикулярно к плоскости параллелограмма (см. рис.).
, и направленный перпендикулярно к плоскости параллелограмма (см. рис.).
 E
E
 C1
C1
C

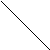

 O B
O B
 |
A D
Скалярное произведение 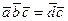 есть произведение модуля вектора
есть произведение модуля вектора 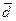 и проекции вектора
и проекции вектора 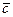 на
на 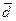 .
.
Высота построенного параллелепипеда есть абсолютная величина этой проекции.
Следовательно, произведение 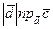 по абсолютной величине равно произведению площади основания параллелепипеда на его высоту, т.е. объему параллелепипеда, построенного на векторах
по абсолютной величине равно произведению площади основания параллелепипеда на его высоту, т.е. объему параллелепипеда, построенного на векторах  ,
,  и
и 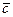 .
.
При этом важно отметить, что скалярное произведение 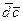 дает объем параллелепипеда иногда с положительным, а иногда с отрицательным знаком. Положительный знак получается, если угол между векторами
дает объем параллелепипеда иногда с положительным, а иногда с отрицательным знаком. Положительный знак получается, если угол между векторами 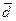 и
и 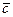 острый; отрицательный – если тупой.
острый; отрицательный – если тупой.
Таким образом, смешанное произведение 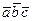 есть число, абсолютная величина которого выражает объем параллелепипеда, построенного на векторах
есть число, абсолютная величина которого выражает объем параллелепипеда, построенного на векторах  ,
,  ,
, 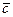 как на ребрах
как на ребрах
Знак произведения положителен, если векторы  ,
,  ,
, 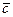 образуют систему, одноименную с основной, и отрицателен в противном случае.
образуют систему, одноименную с основной, и отрицателен в противном случае.
Абсолютная величина смешанного произведения остается той же, в каком бы порядке мы ни брали сомножители. Что касается знака, то он будет в одних случаях положительным, в других – отрицательным; это зависит от того, образуют ли наши три вектора, взятые в определенном порядке, систему одноименную с основной, или нет. Заметим, что у нас оси расположены так, что они следуют одна за другой против часовой стрелки, если смотреть во внутреннюю часть трехгранного угла. Порядок следования не нарушается, если мы начнем обход со второй оси или с третьей, лишь бы он совершался в том же направлении, т.е. против часовой стрелки. При этом множители переставляются в круговом порядке (циклически). Таким образом, получается следующее свойство:
Смешанное произведение не меняется при круговой (циклической) перестановке его сомножителей. Перестановка двух соседних сомножителей меняет знак произведения:
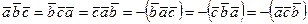 .
.
Наконец, из геометрического смысла смешанного произведения непосредственно следует следующее утверждение.
Необходимым и достаточным условием компланарности векторов  ,
,  ,
, 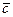 является равенство нулю их смешанного произведения:
является равенство нулю их смешанного произведения:
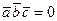 .
.
Дата добавления: 2020-11-15; просмотров: 70; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
