Транспортная задача с правильным балансом
ПРИМЕР № 1: Решить транспортную задачу (т.е. найти минимально возможную общую стоимость всех перевозок), исходные данные которой представлены в табл. 6.1.1:
Таблица 6.1.1
| Потребители | ||||||
| Поставщики | bj | 80 | 120 | 160 | 120 | |
| ai | ||||||
| 120 | 1 | 3 | 4 | 2 | ||
| 160 | 4 | 5 | 8 | 3 | ||
| 200 | 2 | 3 | 6 | 7 | ||
Алгоритм решения транспортной задачи
1) Первым делом нужно определить вид математической модели задачи, просуммировав запасы и потребности:
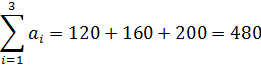

В данном примере 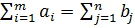 (480=480), следовательно, задача имеет закрытую модель.
(480=480), следовательно, задача имеет закрытую модель.
2) Далее определяем общее количество перевозок по формуле вычисления ранга системы ограничений: 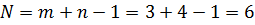 , следовательно в данном примере общее количество перевозок может быть не более 6.
, следовательно в данном примере общее количество перевозок может быть не более 6.
3) Составляем первое опорное решение с помощью одного из методов построения начального опорного решения – метода северо-западного угла (рис. 6.1.1) или метода минимальной стоимости (рис. 6.1.2).
Метод северо-западного угла
Это наиболее простой метод построения начального опорного решения транспортной задачи. В данном методе запасы очередного по номеру поставщика используются для обеспечения запросов очередных по номеру потребителей до тех пор, пока не будут исчерпаны полностью, после чего используются запасы следующего по номеру поставщика.
Заполнение таблицы транспортной задачи начинается с левого верхнего угла, поэтому этот метод и называется методом северо-западного угла. Этот метод состоит из ряда однотипных шагов, на каждом из которых, исходя из запасов очередного поставщика и запросов очередного потребителя, заполняется только одна клетка и соответственно исключается из рассмотрения (вычёркивается) один поставщик или один потребитель.
|
|
|
Если в очередную клетку таблицы (i , j) требуется поставить перевозку, а поставщик с номером i или потребитель с номером j имеет нулевые запасы или запросы, то ставится в клетку перевозка, равная нулю (базисный нуль), и после этого исключается из рассмотрения либо соответствующий поставщик, либо потребитель.[2]
1 шаг: 2 шаг:

3 шаг: 4 шаг:
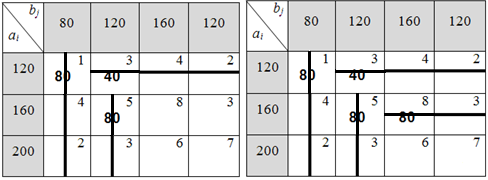
5 шаг: 6 шаг:

Рисунок 6.1.1. Построение начального опорного решения методом северо-западного угла.
Метод минимальной стоимости
Метод минимальной стоимости позволяет построить начальное опорное решение, достаточно близкое к оптимальному, т.к. использует матрицу стоимостей транспортной задачи. Он состоит из ряда шагов, на каждом из которых заполняется только одна клетка таблицы, соответствующая минимальной стоимости 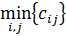 , и исключается из рассмотрения только одна строка (поставщик) или один столбец (потребитель).
, и исключается из рассмотрения только одна строка (поставщик) или один столбец (потребитель).
|
|
|
Поставщик исключается из рассмотрения, если его запасы груза использованы полностью. Потребитель исключается из рассмотрения, если его запросы удовлетворены полностью. При этом, если поставщик ещё не исключён, но его запасы равны нулю, то на том шаге, когда от данного поставщика требуется поставить груз, в соответствующую клетку таблицы заносится базисный нуль, и лишь затем поставщик исключается из рассмотрения. Аналогично исключается потребитель.[1]
1 шаг: 2 шаг:

3 шаг: 4 шаг:

5 шаг: 6 шаг:
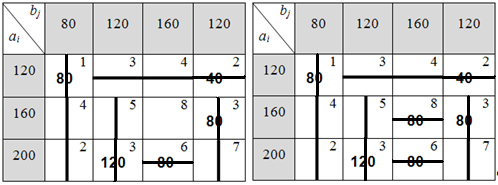
Рисунок 6.1.2. Построение начального опорного решения методом минимальной стоимости.
Далее решаем задачу на основании начального опорного решения, построенного методом минимальной стоимости, т.к. этот метод даёт опорное решение, более приближённое к оптимальному (что позволяет сократить количество дальнейших итераций решения задачи).
Вычисляем первоначальную общую стоимость всех перевозок:

Цель решения транспортной задачи – уменьшение первоначальной общей стоимости перевозок (т.е. экономия средств на перевозку грузов).
|
|
|
4) Дальнейшее решение транспортной задачи основано на отыскании оптимального решения с помощью метода потенциалов.
Метод потенциалов
Этот метод позволяет упростить наиболее трудоёмкую часть вычислений транспортной задачи – нахождение оценок разложения векторов по базису для свободных клеток таблицы (т.е. признаков оптимальности решения).
В данном методе каждое ограничение задачи содержит только две переменные, т.к. каждый вектор-условие системы ограничений исходной задачи имеет только две отличные от нуля координаты. Условий неотрицательности задача с правильным балансом не имеет, т.к. все ограничения в исходной задаче – равенства.
Если допустимое решение  транспортной задачи не является оптимальным, то существуют потенциалы (возможности улучшения) поставщиков
транспортной задачи не является оптимальным, то существуют потенциалы (возможности улучшения) поставщиков 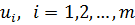 и потребителей
и потребителей  удовлетворяющие следующим условиям:
удовлетворяющие следующим условиям:


Эта группа равенств используется как система уравнений для нахождения потенциалов. Данная система уравнений имеет т+п неизвестных 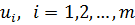 и
и 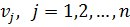 . Количество уравнений системы, как и количество отличных от нуля координат опорного решения, равно N = m + n -1. А так как количество неизвестных системы на единицу больше количества уравнений, то одной из них можно задать значение произвольно (равной нулю), а остальные найти из системы.[3]
. Количество уравнений системы, как и количество отличных от нуля координат опорного решения, равно N = m + n -1. А так как количество неизвестных системы на единицу больше количества уравнений, то одной из них можно задать значение произвольно (равной нулю), а остальные найти из системы.[3]
|
|
|
Таким образом, расставляем потенциалы для проверки оптимальности решения, начиная с нуля около любой клетки поставщика (табл. 6.1.2), и вычисляем остальные потенциалы с помощью системы уравнений только по занятым клеткам: 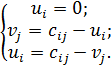 (табл. 6.1.3):
(табл. 6.1.3):
Таблица 6.1.2
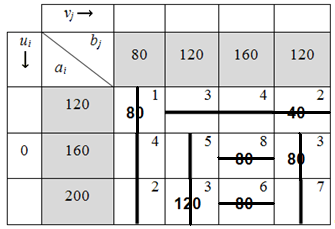
Вычисляем потенциалы по занятым клеткам:

После проведённых расчётов получаем следующую таблицу:
Таблица 6.1.3
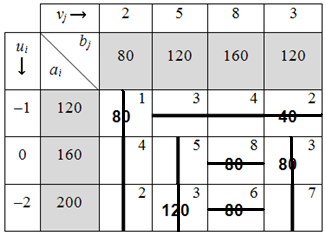
5) Далее нужно найти оценки разложения векторов по базису для свободных клеток таблицы транспортной задачи. Признак оптимальности решения можно сформулировать так же, как и в симплекс-методе (для задачи на минимум): опорное решение является оптимальным, если для всех векторов-условий оценки неположительные ( 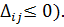 Таким образом, решение не является оптимальным, пока найдётся хотя бы одна оценка
Таким образом, решение не является оптимальным, пока найдётся хотя бы одна оценка 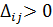 , которую нужно отметить в таблице (табл. 6.1.4).
, которую нужно отметить в таблице (табл. 6.1.4).
Оценки свободных клеток вычисляются по формуле:
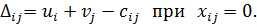
В нашем примере оценки свободных клеток будут следующими:

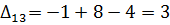

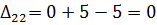

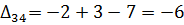
Так как  , то отмечаем их в таблице (табл. 6.1.4):
, то отмечаем их в таблице (табл. 6.1.4):
Таблица 6.1.4
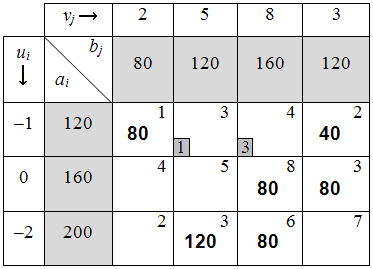
6) Среди отмеченных в таблице оценок нужно выбрать наибольшую (в нашем примере выбираем 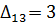 ). Если несколько отмеченных в таблице оценок равны, то нужно выбрать ту, в клетке которой проставлена наименьшая цена за перевозку. Начиная с выбранной клетки строится цикл.
). Если несколько отмеченных в таблице оценок равны, то нужно выбрать ту, в клетке которой проставлена наименьшая цена за перевозку. Начиная с выбранной клетки строится цикл.
Цикл
Циклом называется такая последовательность клеток таблицы транспортной задачи 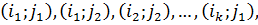 в которой две и только две соседние клетки расположены в одной строке или в одном столбце, причём первая и последняя клетки также находятся в одной строке или столбце. В транспортной задаче цикл всегда один и строится он, начиная с выбранной свободной клетки, только по занятым клеткам.
в которой две и только две соседние клетки расположены в одной строке или в одном столбце, причём первая и последняя клетки также находятся в одной строке или столбце. В транспортной задаче цикл всегда один и строится он, начиная с выбранной свободной клетки, только по занятым клеткам.
Цикл изображают в таблице транспортной задачи в виде замкнутой ломаной линии. В цикле любая клетка является угловой, в которой происходит поворот звена ломаной линии на 90о.
В начальной клетке цикла ставится знак «+», а далее знаки чередуются («+»/«–») по углам цикла (табл. 6.1.5).[1]
Таблица 6.1.5. Построение цикла.
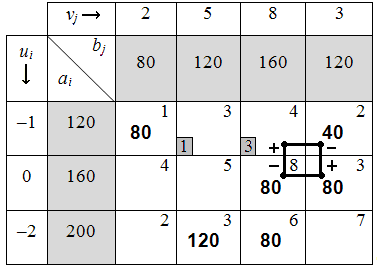
7) Для дальнейшего решения задачи среди клеток со знаком «–» нужно выбрать клетку с наименьшим количеством перевозимой продукции (в нашем примере выбираем клетку14 с количеством продукции 40 ед.). Если в таблице одновременно находятся несколько клеток с равными количествами перевозимой продукции, то выбираем клетку с наибольшей ценой за перевозку. Далее осуществляем сдвиг продукции по циклу.
Сдвигом продукции по циклу на минимальную величину перевозок называется увеличение объёмов перевозок во всех клетках цикла, отмеченных знаком «+», и уменьшение объёмов перевозок во всех клетка цикла, отмеченных знаком «–» на эту минимальную величину. Таким образом происходит перераспределение перевозимой продукции, за счёт чего уменьшается общая стоимость всех перевозок (табл. 6.1.6).
Из клетки с выбранным минимальным количеством перевозимой продукции (40 ед.) продукция вывозится полностью, а в случае наличия нескольких клеток с таким же перевозимым количеством продукция вывозится, оставляя в клетках за собой базисные нули (для того, чтобы суммарное количество перевозок не изменялось).
Таблица 6.1.6. Перераспределение продукции.
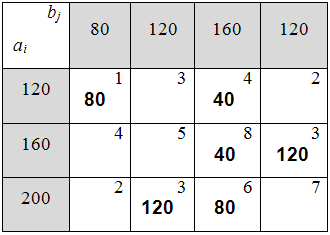
Вычисляем значение целевой функции на текущей итерации:
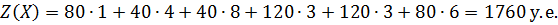
Из проведённого расчёта видно, что значение целевой функции после проведённого перераспределения продукции уменьшилось по сравнению со значением на опорном плане. Таким образом, экономия средств составила 
8) Далее продолжаем решение с пункта № 4 до тех пор, пока все оценки оптимальности не станут неположительными  Тогда значение целевой функции будет являться оптимальным (т.е. общая стоимость всех перевозок будет минимально возможной).
Тогда значение целевой функции будет являться оптимальным (т.е. общая стоимость всех перевозок будет минимально возможной).
В нашем примере заново вычисляем потенциалы, начиная с 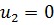 (табл. 6.1.7):
(табл. 6.1.7):
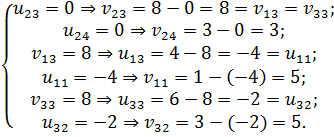
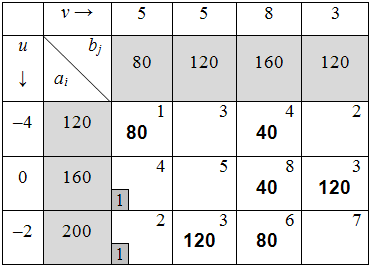
Таблица 6.1.7

Далее вычисляем оценки оптимальности решения для свободных клеток:


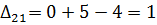
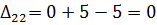

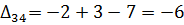
Так как  , то отмечаем их в таблице (табл. 6.1.8):
, то отмечаем их в таблице (табл. 6.1.8):
Таблица 6.1.8
Так как 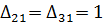 , для построения цикла выбираем клетку31 (её цена за перевозку продукции меньше). Строим цикл (табл. 6.1.9):
, для построения цикла выбираем клетку31 (её цена за перевозку продукции меньше). Строим цикл (табл. 6.1.9):
Таблица 6.1.9
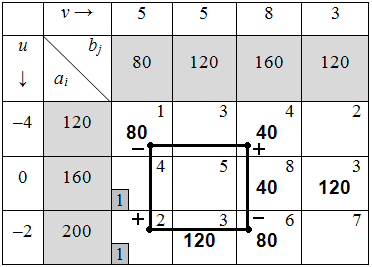
Среди клеток со знаком «–» выбираем наименьшее количество продукции (80 ед.). В клетке11 и в клетке33 количества продукции равны, следовательно, выбираем клетку33, т.к. цена за перевозку продукции в ней больше. Далее перераспределяем продукцию, сдвинув её по циклу (табл. 6.1.10):
Таблица 6.1.10
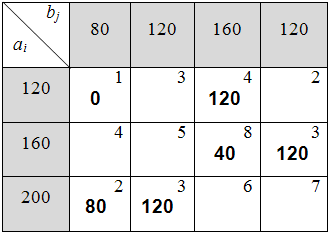
Вычисляем значение целевой функции на текущей итерации:
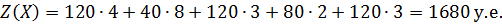
Из проведённого расчёта видно, что значение целевой функции после проведённого перераспределения продукции уменьшилось по сравнению со значением на предыдущей итерации. Таким образом, экономия средств составила 
Далее заново вычисляем потенциалы, начиная с 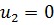 (табл. 6.1.11):
(табл. 6.1.11):

Таблица 6.1.11
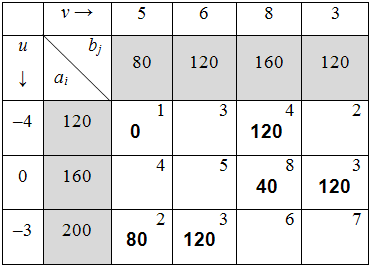
Далее вычисляем оценки оптимальности решения для свободных клеток:


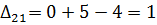

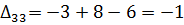
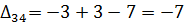
Так как 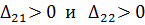 , то отмечаем их в таблице (табл. 6.1.12):
, то отмечаем их в таблице (табл. 6.1.12):
Таблица 6.1.12

Так как 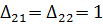 , для построения цикла выбираем клетку21 (её цена за перевозку продукции меньше). Строим цикл (табл. 6.1.13):
, для построения цикла выбираем клетку21 (её цена за перевозку продукции меньше). Строим цикл (табл. 6.1.13):
Таблица 6.1.13
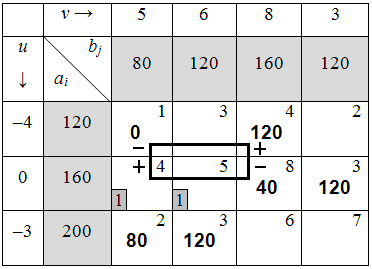
Среди клеток со знаком «–» выбираем наименьшее количество продукции (0 ед.) и перераспределяем продукцию, сдвинув её по циклу (табл. 6.1.14):
Таблица 6.1.14
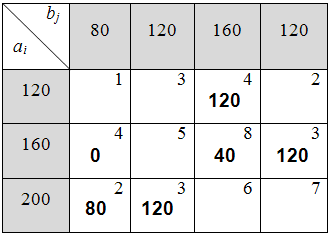
Так как в перераспределении продукции участвовал базисный нуль, значение целевой функции вычислять не нужно (оно не поменялось).
Снова вычисляем потенциалы, начиная с 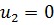 (табл. 6.1.15):
(табл. 6.1.15):
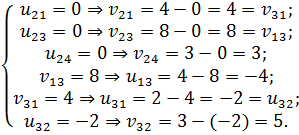
Таблица 6.1.15

Далее вычисляем оценки оптимальности решения для свободных клеток:



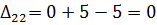
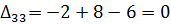
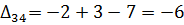
Так как все оценки  , следовательно, найденное решение является оптимальным. Выписываем ответ:
, следовательно, найденное решение является оптимальным. Выписываем ответ:
Ответ: 
6.2. Транспортная задача с неправильным балансом
ПРИМЕР № 1: Решить транспортную задачу (т.е. найти минимально возможную общую стоимость всех перевозок), исходные данные которой представлены в табл. 6.2.1[7]:
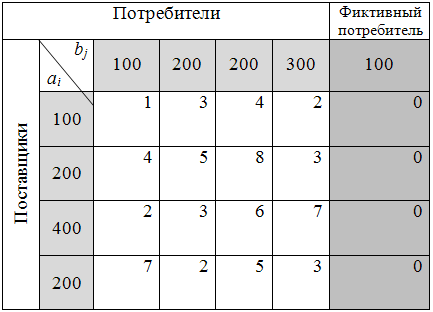
Таблица 6.2.1
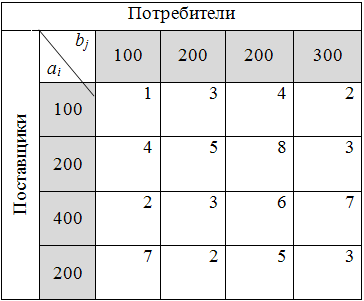
Алгоритм решения:
1) Первым делом нужно определить вид математической модели задачи, просуммировав запасы и потребности:
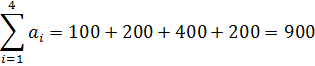

В данном примере суммарные запасы поставщиков больше суммарных запросов потребителей: 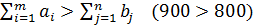 , следовательно, задача имеет открытую модель.
, следовательно, задача имеет открытую модель.
Чтобы задача в рассматриваемом случае имела решение, необходимо ввести фиктивного (ненастоящего) потребителя с недостающим объёмом запросов  ед. и нулевыми стоимостями перевозок единиц груза
ед. и нулевыми стоимостями перевозок единиц груза 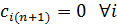 (табл. 6.2.2).
(табл. 6.2.2).
Аналогично поступают в случае, когда суммарные запросы потребителей превосходят суммарные запасы поставщиков (т.е. вводят фиктивного поставщика с нулевыми ценами за перевозки).
Необходимо отметить, что при составлении начального опорного решения в последнюю очередь следует распределять запасы фиктивного поставщика или удовлетворять запросы фиктивного потребителя, несмотря на то, что им соответствует наименьшая стоимость перевозок, равная нулю (иначе решение будет иметь лишние итерации).
Таблица 6.2.2
2) Далее транспортная задача решается аналогично задаче с правильным балансом. Определяем общее количество перевозок по формуле вычисления ранга системы ограничений: 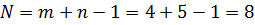 , следовательно, в данном примере общее количество перевозок может быть не более 8.
, следовательно, в данном примере общее количество перевозок может быть не более 8.
3) Составляем первое опорное решение с помощью метода минимальной стоимости (табл. 6.2.3):
Таблица 6.2.3

Вычисляем первоначальную общую стоимость всех перевозок:

4) Дальнейшее решение транспортной задачи основано на отыскании оптимального решения с помощью метода потенциалов. В нашем примере вычисляем потенциалы, начиная с 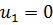 (табл. 6.2.4):
(табл. 6.2.4):
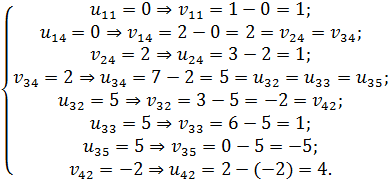
Таблица 6.2.4

5) Далее нужно найти оценки разложения векторов по базису для свободных клеток таблицы транспортной задачи. В нашем примере оценки свободных клеток будут следующими:
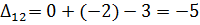


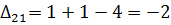

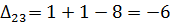
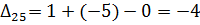

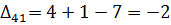
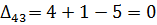

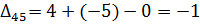
Так как 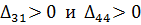 , то отмечаем их в таблице (табл. 6.2.5):
, то отмечаем их в таблице (табл. 6.2.5):
Таблица 6.2.5
6) Среди отмеченных в таблице оценок нужно выбрать наибольшую (в нашем примере выбираем 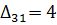 ), построить цикл и расставить знаки по углам цикла (табл. 6.2.6):
), построить цикл и расставить знаки по углам цикла (табл. 6.2.6):
Таблица 6.2.6

7) Для дальнейшего решения задачи среди клеток со знаком «–» нужно выбрать клетку с наименьшим количеством перевозимой продукции. В нашем примере выбираем клетку34 (т.к. в ней цена за перевозку больше) и осуществляем сдвиг продукции по циклу (табл. 6.2.7):
Таблица 6.2.7
Вычисляем общую стоимость всех перевозок на текущей итерации:
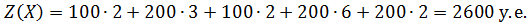
8) Далее продолжаем решение с пункта № 4 до тех пор, пока все оценки оптимальности не станут неположительными  Тогда значение целевой функции будет являться оптимальным (т.е. общая стоимость всех перевозок будет минимально возможной).
Тогда значение целевой функции будет являться оптимальным (т.е. общая стоимость всех перевозок будет минимально возможной).
В нашем примере заново вычисляем потенциалы, начиная с 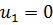 (табл. 6.2.8):
(табл. 6.2.8):
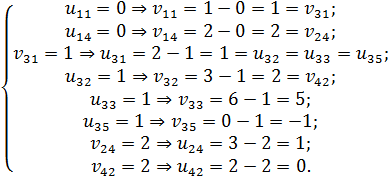
Таблица 6.2.8
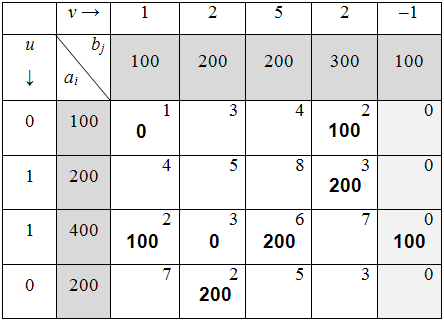
Далее вычисляем оценки оптимальности решения для свободных клеток:
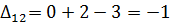

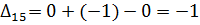
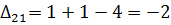
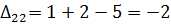

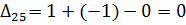
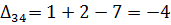
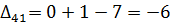

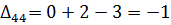

Так как 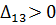 , то отмечаем её в таблице и строим цикл (табл. 6.2.9):
, то отмечаем её в таблице и строим цикл (табл. 6.2.9):
Таблица 6.2.9
Среди клеток со знаком «–» нужно выбрать клетку с наименьшим количеством перевозимой продукции (0 ед.) и осуществить сдвиг продукции по циклу (табл. 6.2.10).
Таблица 6.2.10
Так как в перераспределении продукции участвовал базисный нуль, значение целевой функции вычислять не нужно (оно не поменялось).
Снова вычисляем потенциалы, начиная с 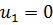 (табл. 6.2.11):
(табл. 6.2.11):
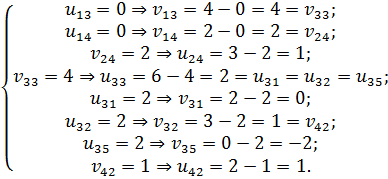
Таблица 6.2.11
Далее вычисляем оценки оптимальности решения для свободных клеток:
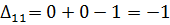

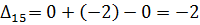
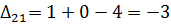
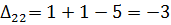
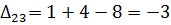

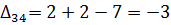

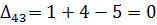
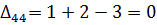

Так как все оценки  , следовательно, найденное решение является оптимальным. Выписываем ответ:
, следовательно, найденное решение является оптимальным. Выписываем ответ:
Ответ: 
6.3. Транспортная задача с ограничениями на пропускную способность
Подобные задачи возникают в тех случаях, когда требуется ограничить перевозки от некоторого поставщика некоторому потребителю (в случае задолженности, его фиксированного спроса и т.п.) или, наоборот, когда требуется зарезервировать некоторый объём перевозимой продукции (в случае предоплаты, предыдущей недопоставки и т.п.).
В транспортной задаче возможны ограничения двух типов:
1) Резервирование перевозки: если  , то необходимо прежде, чем решать задачу, сократить (уменьшить) запасы данного i-го поставщика и запросы данного j-го потребителя на величину а (т.е. зарезервировать перевозку в количестве а ед.). После решения задачи, в найденном оптимальном решении следует увеличить объём перевозки xij на величину а.
, то необходимо прежде, чем решать задачу, сократить (уменьшить) запасы данного i-го поставщика и запросы данного j-го потребителя на величину а (т.е. зарезервировать перевозку в количестве а ед.). После решения задачи, в найденном оптимальном решении следует увеличить объём перевозки xij на величину а.
2) Ограничение перевозки: если 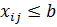 , то необходимо вместо данного j-го потребителя с запросами bj ввести двух других потребителей. Один из них, с номером j, должен иметь заданную величину ограничения на запрос b, а другой (фиктивный потребитель) – запрос
, то необходимо вместо данного j-го потребителя с запросами bj ввести двух других потребителей. Один из них, с номером j, должен иметь заданную величину ограничения на запрос b, а другой (фиктивный потребитель) – запрос 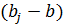 . Стоимости перевозок у них остаются прежними, за исключением стоимости cij у фиктивного потребителя, которая стремится к бесконечности
. Стоимости перевозок у них остаются прежними, за исключением стоимости cij у фиктивного потребителя, которая стремится к бесконечности  по аналогии с методом искусственного базиса. После решения задачи, в найденном оптимальном решении количества грузов, перевозимых фиктивному потребителю, прибавляются к bj (т.е. столбцы обратно складываются в один).
по аналогии с методом искусственного базиса. После решения задачи, в найденном оптимальном решении количества грузов, перевозимых фиктивному потребителю, прибавляются к bj (т.е. столбцы обратно складываются в один).
Так как 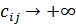 – самая большая стоимость перевозки, то в оптимальном решении клетка с этим номером всегда остаётся пустой, поэтому после обратного объёдинения столбцов объём перевозки xij никогда не превзойдёт заданного ограничения b.
– самая большая стоимость перевозки, то в оптимальном решении клетка с этим номером всегда остаётся пустой, поэтому после обратного объёдинения столбцов объём перевозки xij никогда не превзойдёт заданного ограничения b.
В некоторых задачах требуется запретить перевозки от отдельных поставщиков отдельным потребителям. В таких случаях также назначают соответствующую этой клетке стоимость перевозки единицы груза 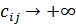 , чтобы данная клетка всегда оставалась пустой.[1]
, чтобы данная клетка всегда оставалась пустой.[1]
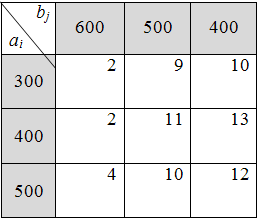
ПРИМЕР № 1: Решить транспортную задачу (табл. 6.3.1), исходные данные которой приведены в табл. 1, при дополнительных условиях: объём перевозки груза от 2-го поставщика 2-му потребителю должен быть не менее 200 ед. продукции  , а от 3-го поставщика 1-му потребителю – не более 300 ед. продукции
, а от 3-го поставщика 1-му потребителю – не более 300 ед. продукции 
Таблица 6.3.1
Алгоритм решения:
1) Для того, чтобы в оптимальном решении объём перевозки х22 был не менее 200 ед. продукции, нужно уменьшить запасы 2-го поставщика и запросы 2-го потребителя на 200 ед. (рис. 6.3.1):
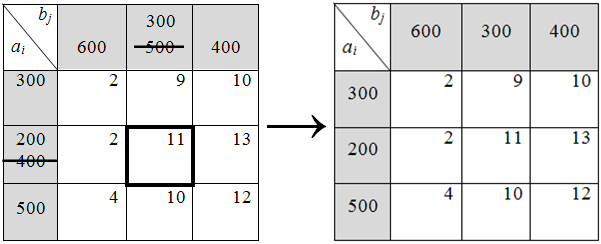
Рисунок 6.3.1. Резервирование перевозки.
2) Для того, чтобы удовлетворить требованию 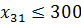 , вместо 1-го потребителя введём двух других. Один из них под прежним первым номером будет иметь запросы в количестве
, вместо 1-го потребителя введём двух других. Один из них под прежним первым номером будет иметь запросы в количестве 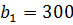 ед. и прежние стоимости перевозок. Другому присвоим №4 (по порядку). Его запросы будут равны
ед. и прежние стоимости перевозок. Другому присвоим №4 (по порядку). Его запросы будут равны  ед. и стоимости перевозок единиц груза те же, что и у 1-го потребителя, за исключением с34, которая стремится к бесконечности:
ед. и стоимости перевозок единиц груза те же, что и у 1-го потребителя, за исключением с34, которая стремится к бесконечности: 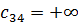 . В результате указанных преобразований таблица исходных данных задачи будет иметь вид (табл. 6.3.2):
. В результате указанных преобразований таблица исходных данных задачи будет иметь вид (табл. 6.3.2):
Таблица 6.3.2
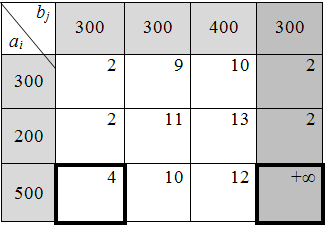
3) Далее решаем транспортную задачу обычным методом. Определяем вид математической модели задачи, просуммировав запасы и потребности:
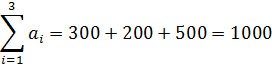
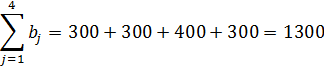
В данном примере суммарные запасы поставщиков меньше суммарных запросов потребителей:  , следовательно, задача имеет открытую модель.
, следовательно, задача имеет открытую модель.
Чтобы задача в рассматриваемом случае имела решение, необходимо ввести фиктивного поставщика с недостающим объёмом запасов 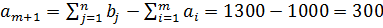 ед. и нулевыми стоимостями перевозок единиц груза
ед. и нулевыми стоимостями перевозок единиц груза 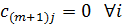 (табл. 6.3.3):
(табл. 6.3.3):
Таблица 6.3.3
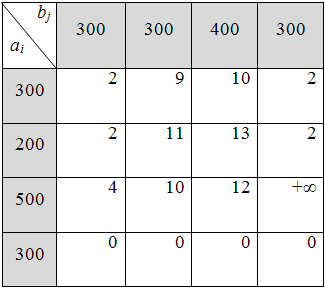
4) Далее транспортная задача решается аналогично задаче с правильным балансом. Определяем общее количество перевозок по формуле вычисления ранга системы ограничений: 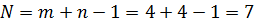 , следовательно, общее количество перевозок может быть не более 7.
, следовательно, общее количество перевозок может быть не более 7.
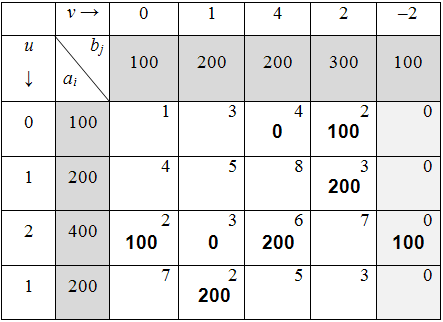
5) Составляем первое опорное решение с помощью метода минимальной стоимости (табл. 6.3.4):
Таблица 6.3.4
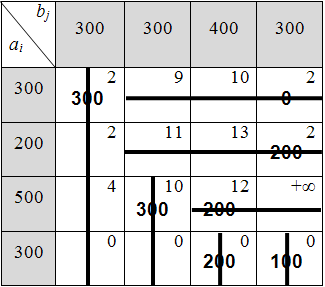
Вычисляем первоначальную общую стоимость всех перевозок:

6) Дальнейшее решение транспортной задачи основано на отыскании оптимального решения с помощью метода потенциалов. В нашем примере вычисляем потенциалы, начиная с 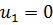 (табл. 6.3.5):
(табл. 6.3.5):
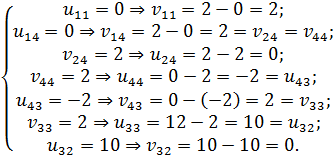
Таблица 6.3.5
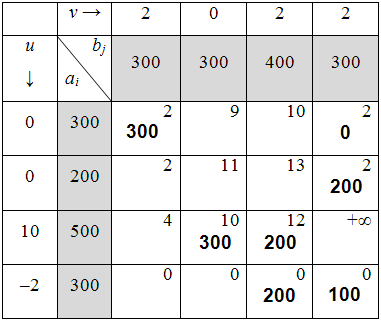
7) Далее нужно найти оценки разложения векторов по базису для свободных клеток таблицы транспортной задачи. В нашем примере оценки свободных клеток будут следующими:
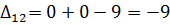
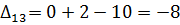
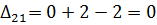

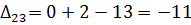
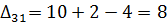
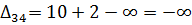
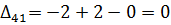
Так как  , то отмечаем её в таблице и строим цикл (табл. 6.3.6):
, то отмечаем её в таблице и строим цикл (табл. 6.3.6):
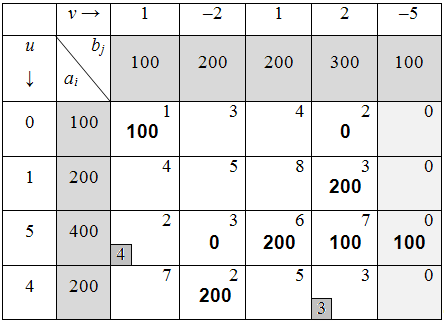
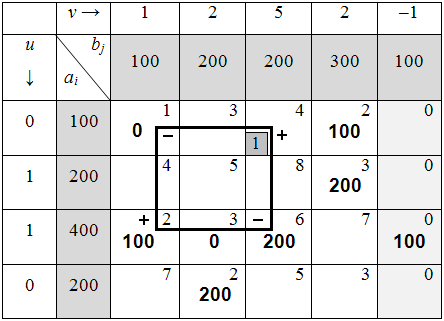
Таблица 6.3.6
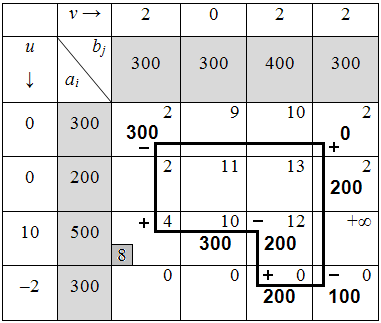
8) Для дальнейшего решения задачи среди клеток со знаком «–» нужно выбрать клетку44 с наименьшим количеством перевозимой продукции (100 ед.) и осуществить сдвиг продукции по циклу (табл. 6.3.7):
Таблица 6.3.7
Вычисляем общую стоимость всех перевозок на текущей итерации:
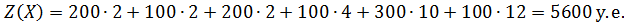
9) Далее продолжаем решение с пункта № 6 до тех пор, пока все оценки оптимальности не станут неположительными  Тогда значение целевой функции будет являться оптимальным (т.е. общая стоимость всех перевозок будет минимально возможной).
Тогда значение целевой функции будет являться оптимальным (т.е. общая стоимость всех перевозок будет минимально возможной).
В нашем примере заново вычисляем потенциалы, начиная с 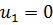 (табл. 6.3.8):
(табл. 6.3.8):
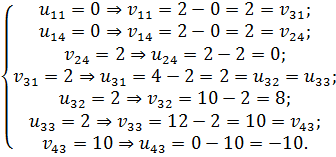
Таблица 6.3.8
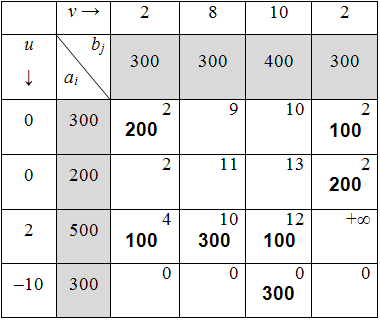
Далее вычисляем оценки оптимальности решения для свободных клеток:

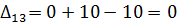
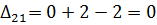

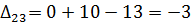
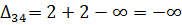

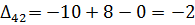
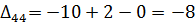
Так как все оценки  , следовательно, найденное решение является оптимальным.
, следовательно, найденное решение является оптимальным.
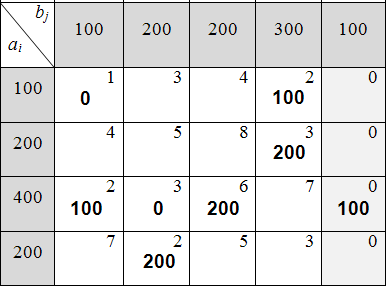
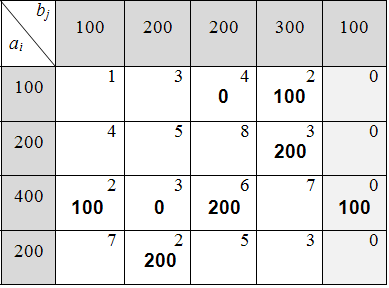
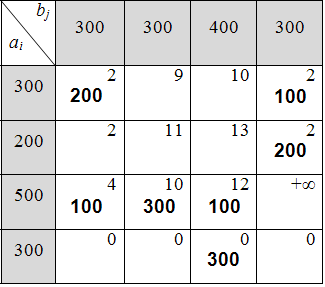
10) Для соблюдения заданных ограничений нужно в клетку22 вернуть 200 ед. продукции (зарезервированной в пункте № 1), объединить столбцы № 1 и № 4 и убрать фиктивного поставщика (табл. 6.3.9):
Таблица 6.3.9

Вычисляем итоговую стоимость всех перевозок:
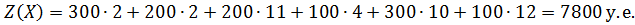
Ответ: 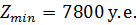
6.4. Транспортная задача по критерию минимума времени
Задача по критерию времени возникает при перевозке срочных грузов. Как и в обычной транспортной задаче имеется т поставщиков с запасами однородного груза в количествах 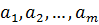 и п потребителей, которым этот груз должен быть доставлен в объёмах
и п потребителей, которым этот груз должен быть доставлен в объёмах 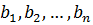 . Известны также
. Известны также 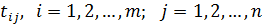 – интервалы времени, за которые грузы доставляются от поставщиков потребителям. Требуется составить такой план перевозок, при котором запасы всех поставщиков вывозятся полностью, запросы всех потребителей удовлетворяются полностью и наибольшее время доставки всех грузов является минимальным.
– интервалы времени, за которые грузы доставляются от поставщиков потребителям. Требуется составить такой план перевозок, при котором запасы всех поставщиков вывозятся полностью, запросы всех потребителей удовлетворяются полностью и наибольшее время доставки всех грузов является минимальным.
Математическая модель транспортной задачи по критерию минимума времени
Пусть 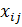 – объём перевозимого груза от i-го поставщика j-му потребителю. Система ограничений рассматриваемой задачи не отличается от системы ограничений обычной транспортной задачи. Допустим,
– объём перевозимого груза от i-го поставщика j-му потребителю. Система ограничений рассматриваемой задачи не отличается от системы ограничений обычной транспортной задачи. Допустим, 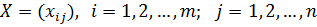 – некоторое допустимое решение задачи. Для составления целевой функции обозначим через
– некоторое допустимое решение задачи. Для составления целевой функции обозначим через 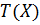 наибольшее значение элементов матрицы
наибольшее значение элементов матрицы  , соответствующих клеткам таблицы, занятым опорным решением:
, соответствующих клеткам таблицы, занятым опорным решением:  . Таким образом, за время
. Таким образом, за время 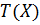 план перевозок будет выполнен полностью. Математическая модель задачи имеет вид (6.4.1)[1]:
план перевозок будет выполнен полностью. Математическая модель задачи имеет вид (6.4.1)[1]:
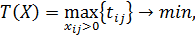
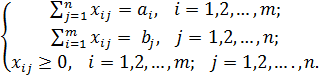 (6.4.1)
(6.4.1)
ПРИМЕР № 1: Найти минимальное время (в часах) на осуществление всех перевозок для задачи, исходные данные которой приведены в табл. 6.4.1:
Таблица 6.4.1

Алгоритм решения:
1) Составляем начальное опорное решение, расставляя количество перевозимой продукции методом северо-западного угла без записи базисных нулей (табл. 6.4.2):
Таблица 6.4.2
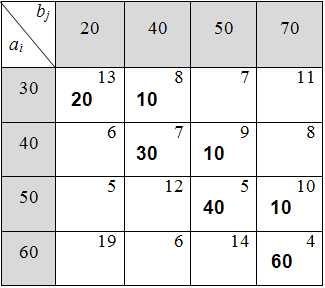
2) Находим максимальное время перевозки среди заполненных клеток:
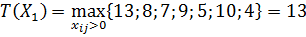 часов.
часов.
3) Перечёркиваем клетки таблицы, в которых время перевозки больше найденного максимального времени, 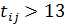 . Занимать эти клетки далее нецелесообразно, т.к. это приведёт к увеличению целевой функции (табл. 6.4.3):
. Занимать эти клетки далее нецелесообразно, т.к. это приведёт к увеличению целевой функции (табл. 6.4.3):
Таблица 6.4.3
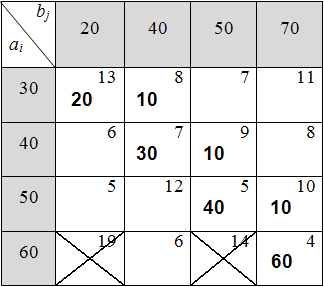
4) Для оптимизации решения необходимо освободить клетку с найденным максимальным временем перевозки (13 ч.) с помощью разгрузочного цикла. Разгрузочные циклы могут быть только квадратного вида с началом в освобождаемой клетке. В каждом разгрузочном цикле, начиная с разгружаемой клетки, расставляются поочерёдно знаки «–» и «+» и осуществляется сдвиг продукции по циклу на минимальное количество, выбранное среди клеток со знаком «–» (по аналогии с решением обычной транспортной задачи) (табл. 6.4.4)[3]:
Таблица 6.4.4
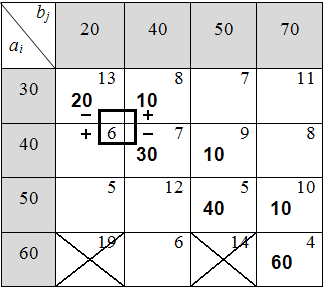
5) После перераспределения продукции транспортная задача будет выглядеть следующим образом (табл. 6.4.5):
Таблица 6.4.5

Снова находим максимальное время перевозки среди заполненных клеток:
 часов.
часов.
6) Продолжаем решение с пункта № 3 до тех пор, пока не исчезнет возможность разгрузить клетку с максимальным временем перевозки. В данном примере перечёркиваем клетки, в которых время перевозки больше найденного максимального времени,  , и строим разгрузочный цикл (табл. 6.4.6):
, и строим разгрузочный цикл (табл. 6.4.6):
Таблица 6.4.6

После перераспределения продукции транспортная задача будет выглядеть следующим образом (табл. 6.4.7):
Таблица 6.4.7
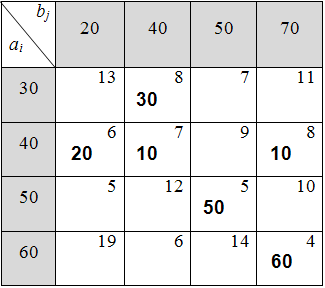
Снова находим максимальное время перевозки среди заполненных клеток:
 часов.
часов.
Далее снова перечёркиваем клетки, в которых время перевозки больше найденного максимального времени, 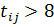 , и строим разгрузочный цикл (табл. 6.4.8):
, и строим разгрузочный цикл (табл. 6.4.8):
Таблица 6.4.8
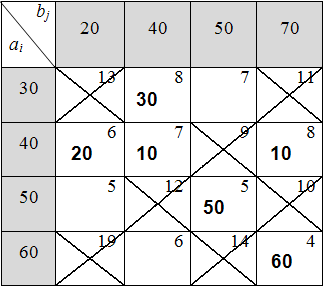
Так как с помощью оставшихся свободных клеток разгрузить клетки с максимальным временем перевозки не удаётся (т.к. нет возможности построить разгрузочный цикл), следовательно, найденное решение транспортной задачи является оптимальным.
Ответ: 
6.5. Задания для самостоятельного решения
Решить транспортные задачи с правильным балансом:
1) 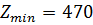

3) 

2) 

4) 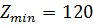
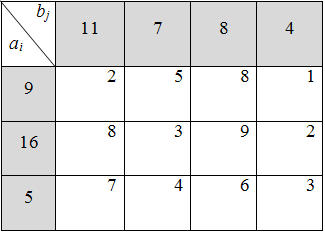
5) 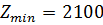
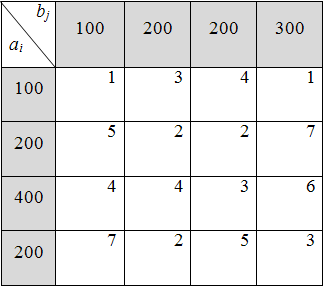
7) 
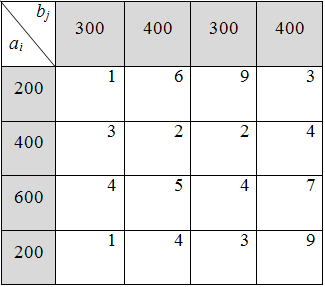
6) 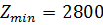
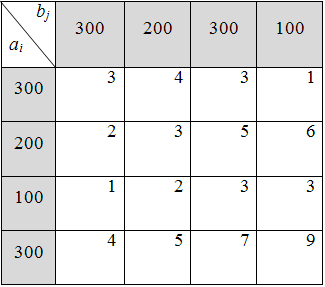
8) 

9) 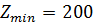

10) 

Решить транспортные задачи с неправильным балансом:
1) 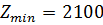

3) 

2) 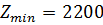
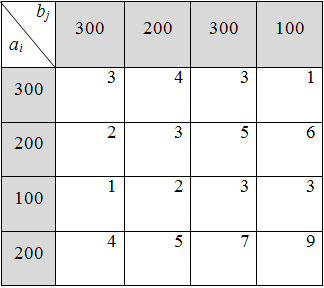
4) 
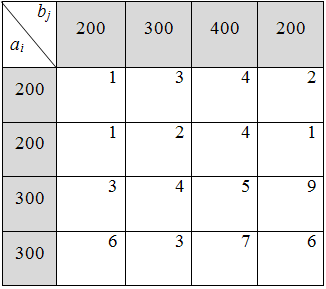
5) 

6) 

7) 

9) 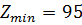
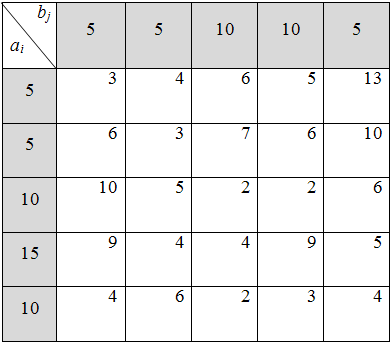
8) 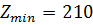

10) 

Решить транспортные задачи с ограничениями на пропускную способность:
1) 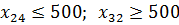
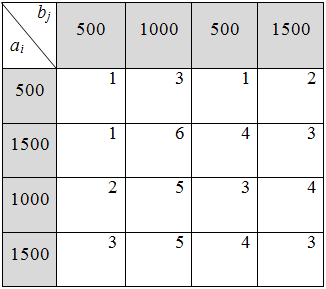
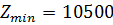
3) 
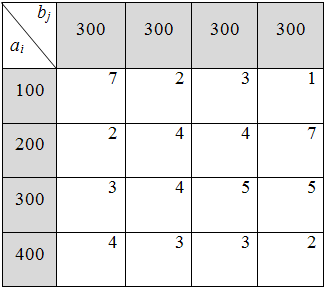
2) 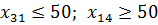


4) 


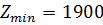
5) 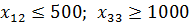


7) 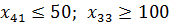
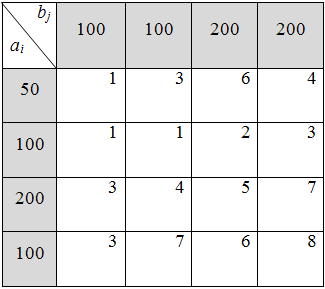
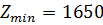
6) 
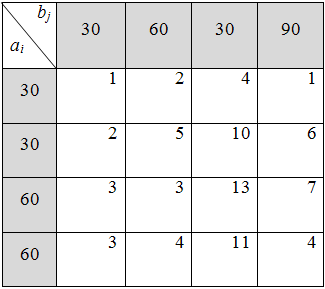
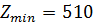
8) 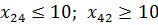
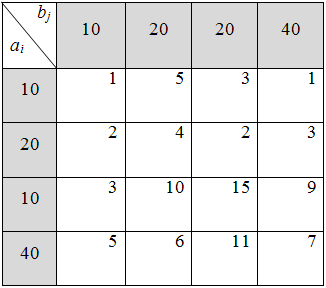
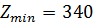
Решить транспортные задачи по критерию минимума времени:
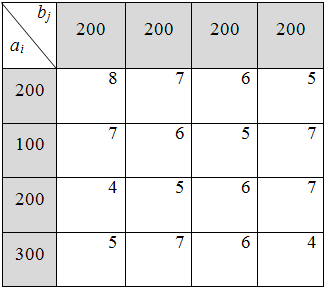
1) 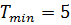
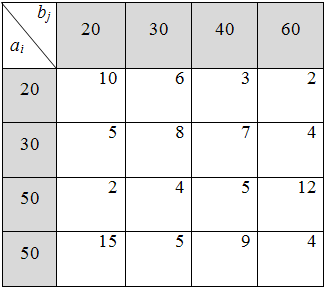
2) 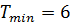
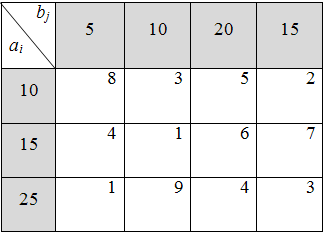
3) 
4) 

Дата добавления: 2020-11-15; просмотров: 1106; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
