Задания для самостоятельного решения
1) 

Ответ: 
2) 

Ответ: 
3) 

Ответ: 
4) 

Ответ: 
5) 

Ответ: 
6) 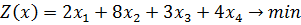

Ответ: 
7) 

Ответ: 
8) 

Ответ: 
9) 

Ответ: 
10) 

Ответ: 
4. Симплекс-метод решения задач линейного программирования
Этот метод состоит в целенаправленном переборе опорных решений задачи линейного программирования. Он позволяет за конечное число шагов расчёта (итераций) либо найти оптимальное решение, либо установить его отсутствие.
Основное содержание симплекс-метода:
1) Нахождение опорного решения;
2) Осуществление перехода к другому опорному решению, на котором значение целевой функции становится ближе к оптимальному;
3) Определение критериев завершения процесса решения задачи, позволяющих своевременно прекратить перебор решений на оптимальном решении или сделать заключение об отсутствии решения ввиду несовместности системы ограничений.[3]
Алгоритм решения задач линейного программирования симплексным методом рассмотрим на следующих примерах.
Задача линейного программирования в канонической форме
ПРИМЕР № 1: 

Алгоритм решения задачи симплекс-методом:
1) Составляем симплексную таблицу. В столбец «Базис» вписываем базисные векторы из системы ограничений (базисные векторы – это векторы, встречающиеся в системе ограничений один раз с коэффициентом «+1», т.е. линейно независимые векторы). В столбец «Х0» вписываем свободные числа системы (правые части всех уравнений, которые должны быть неотрицательны). Далее заполняем таблицу коэффициентами векторов из системы ограничений (табл. 4.1.1):
|
|
|
Таблица 4.1.1
| Базис | х0 | х1 | х2 | х3 | х4 |
| х3 | 2 | –1 | 2 | 1 | 0 |
| х4 | 6 | 3 | –2 | 0 | 1 |
2) Вычисляем оценки разложений векторов системы ограничений по базису, которые являются признаками оптимальности решения, по формуле:
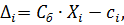
где  - вектор, состоящий из коэффициентов базиса в целевой функции, в данном примере
- вектор, состоящий из коэффициентов базиса в целевой функции, в данном примере  ;
;
 - вектор, состоящий из соответствующих коэффициентов при
- вектор, состоящий из соответствующих коэффициентов при  из системы ограничений, в данном примере
из системы ограничений, в данном примере  ;
;
 - коэффициенты при
- коэффициенты при  в целевой функции, в данном примере
в целевой функции, в данном примере  .
.
Для разбираемой в данном примере задачи оценки разложений векторов будут следующими:





Таким образом, оценки базисных векторов всегда равны 0.
Далее вносим вычисленные оценки в симплексную таблицу (табл. 4.1.2):
Таблица 4.1.2
| Базис | х0 | х1 | х2 | х3 | х4 |
| х3 | 2 | –1 | 2 | 1 | 0 |
| х4 | 6 | 3 | –2 | 0 | 1 |
| Δ | 0 | –7 | 9 | 0 | 0 |
3) В задаче на максимум признаком неоптимальности решения являются отрицательные оценки Δ<0, показывающие, что решение может быть улучшено. В задаче на минимум признаком неоптимальности решения являются положительные оценки Δ>0.
|
|
|
В данном примере задача решается на максимум, поэтому помечаем отрицательную оценку вектора Х1 (табл. 4.1.3):
Таблица 4.1.3
| Базис | х0 | х1 | х2 | х3 | х4 |
| х3 | 2 | –1 | 2 | 1 | 0 |
| х4 | 6 | 3 | –2 | 0 | 1 |
| Δ | 0 | –7 | 9 | 0 | 0 |
4) Для найденных оценок вычисляем вспомогательный параметр  по формуле:
по формуле:  . Для улучшения опорного решения эти вспомогательные параметры должны быть положительными, т.е.
. Для улучшения опорного решения эти вспомогательные параметры должны быть положительными, т.е.  . Если
. Если  то в таблице ставится прочерк, т.к. этот случай является признаком невозможности улучшения опорного решения с помощью замены данного вектора. Если для столбцов с неоптимальными оценками все
то в таблице ставится прочерк, т.к. этот случай является признаком невозможности улучшения опорного решения с помощью замены данного вектора. Если для столбцов с неоптимальными оценками все  то задача имеет неограниченную целевую функцию:
то задача имеет неограниченную целевую функцию: 
В нашем примере вычисляем вспомогательный параметр для оценки вектора Х1:  (в таблице ставим прочерк) и
(в таблице ставим прочерк) и 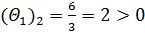 (заносим в таблицу, табл. 4.1.4):
(заносим в таблицу, табл. 4.1.4):
Таблица 4.1.4
| Базис | х0 | х1 | х2 | х3 | х4 | Θ1 |
| х3 | 2 | –1 | 2 | 1 | 0 | – |
| х4 | 6 | 3 | –2 | 0 | 1 | 2 |
| Δ | 0 | –7 | 9 | 0 | 0 |
5) Выбираем минимальный параметр  в каждом столбце (если их несколько) и отмечаем его. В данном примере отмечаем
в каждом столбце (если их несколько) и отмечаем его. В данном примере отмечаем  (табл. 4.1.4).
(табл. 4.1.4).
6) Составляем критерий выбора вектора, вводимого в базис, и вектора, выводимого из него, для наибольшего изменения целевой функции при улучшении опорного решения. В задачах на максимум выбор осуществляется функцией  , а в задачах на минимум – функцией
, а в задачах на минимум – функцией  .
.
|
|
|
В данном примере ничего выбирать не нужно, т.к. у нас только один столбец 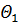 , следовательно, новым базисным вектором будет
, следовательно, новым базисным вектором будет  , и он заменит собой вектор
, и он заменит собой вектор 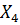 (табл. 4.1.5):
(табл. 4.1.5):
Таблица 4.1.5

7) Далее применяем элементарные преобразования Жордана-Гаусса и приводим выбранный столбец (  ) к базисному виду. При этом разрешающий элемент находится на пересечении выбранного столбца и выбранной строки (в нашем примере он равен 3, табл. 4.1.5). Проведённые расчёты представлены в табл. 4.1.6 (вспомогательный параметр
) к базисному виду. При этом разрешающий элемент находится на пересечении выбранного столбца и выбранной строки (в нашем примере он равен 3, табл. 4.1.5). Проведённые расчёты представлены в табл. 4.1.6 (вспомогательный параметр 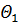 в расчётах не участвует):
в расчётах не участвует):
Таблица 4.1.6
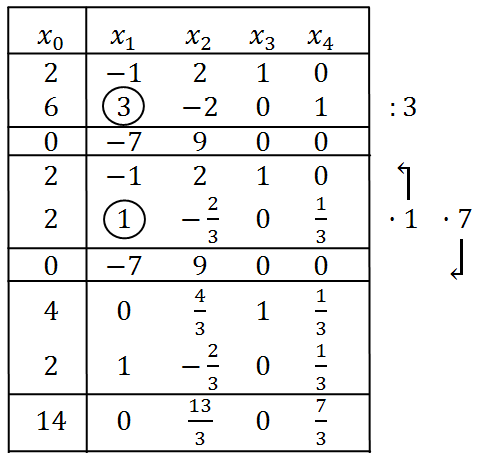
8) После выполнения преобразований симплексная таблица будет выглядеть следующим образом (табл. 4.1.7).
Таблица 4.1.7
| Базис | х0 | х1 | х2 | х3 | х4 | Θ1 |
| х3 | 2 | –1 | 2 | 1 | 0 | – |
| х4 | 6 | 3 | –2 | 0 | 1 | 2 |
| Δ | 0 | –7 | 9 | 0 | 0 | |
| х3 | 4 | 0 | 4/3 | 1 | 1/3 | |
| х1 | 2 | 1 | –2/3 | 0 | 1/3 | |
| Δ | 14 | 0 | 13/3 | 0 | 7/3 |
9) Далее продолжаем решение с нахождения признаков оптимальности решения (пункт № 3 рассматриваемого алгоритма) и продолжаем итерации до тех пор, пока все оценки разложения Δi не будут соответствовать экстремуму задачи.
|
|
|
10) В том случае, если все оценки разложения Δi соответствуют условию задачи, найденное решение является оптимальным, следовательно, выписываем ответ.
В данном примере все коэффициенты в строке оценок Δi положительны на второй итерации (табл. 4.1.7), а задача решается на отыскание максимального значения, следовательно, признак оптимальности решения выполнен. Выписываем ответ из соответствующих ячеек симплексной таблицы (табл. 4.1.8):
Таблица 4.1.8
| Базис | х0 | х1 | х2 | х3 | х4 | Θ1 |
| х3 | 2 | –1 | 2 | 1 | 0 | – |
| х4 | 6 | 3 | –2 | 0 | 1 | 2 |
| Δ | 0 | –7 | 9 | 0 | 0 | |
| х3 | 4 | 0 | 4/3 | 1 | 1/3 | |
| х1 | 2 | 1 | –2/3 | 0 | 1/3 | |
| Δ | 14 | 0 | 13/3 | 0 | 7/3 |
Ответ: 
Замечание : Оптимальное решение задачи линейного программирования является единственным, если для любого вектора системы ограничений, не входящего в базис, оценка разложения  Если в найденном решении существуют
Если в найденном решении существуют  , то нужно найти остальные оптимальные решения задачи, начиная с пункта № 4.
, то нужно найти остальные оптимальные решения задачи, начиная с пункта № 4.
4.2. Задача линейного программирования без начального базиса
В предыдущем рассмотренном примере система ограничений имела начальный базис (векторы х3 и х4) и была представлена в канонической форме. Далее рассмотрим пример задачи, система ограничений которой не имеет начального базиса и представлена в виде системы неравенств.
ПРИМЕР № 1: 

Решение:
1) Данную задачу сначала необходимо представить в канонической форме. Для этого во все неравенства вида «≤» нужно добавить (а из неравенств вида «≥» нужно вычесть) дополнительные переменные с нумерацией в порядке возрастания, которые войдут в целевую функцию с нулевыми коэффициентами (рис. 4.2.1):

Рисунок 4.2.1
После этих действий исходная задача будет представлена в канонической форме записи:

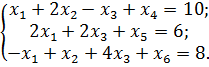
2) Составляем симплексную таблицу. В столбец «Базис» вписываем базисные векторы из системы ограничений (х4, х5 и х6). В столбец «Х0» вписываем свободные числа системы (правые части всех уравнений, которые должны быть неотрицательны). Далее заполняем таблицу коэффициентами векторов из системы ограничений (табл. 4.2.1):
Таблица 4.2.1
| Базис | х0 | х1 | х2 | х3 | х4 | х5 | х6 |
| х4 | 10 | 1 | 2 | –1 | 1 | 0 | 0 |
| х5 | 6 | 2 | 0 | 2 | 0 | 1 | 0 |
| х6 | 8 | –1 | 1 | 4 | 0 | 0 | 1 |
3) Вычисляем оценки разложений векторов системы ограничений по базису:

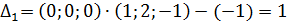



Далее вносим вычисленные оценки в симплексную таблицу (табл. 4.2.2). В данном примере задача решается на минимум, поэтому помечаем положительные оценки векторов (х1 и х2):
Таблица 4.2.2
| Базис | х0 | х1 | х2 | х3 | х4 | х5 | х6 |
| х4 | 10 | 1 | 2 | –1 | 1 | 0 | 0 |
| х5 | 6 | 2 | 0 | 2 | 0 | 1 | 0 |
| х6 | 8 | –1 | 1 | 4 | 0 | 0 | 1 |
| Δ | 0 | 1 | 1 | –2 | 0 | 0 | 0 |
4) Для найденных оценок вычисляем вспомогательные параметры и заносим их в симплексную таблицу (табл. 4.2.3):






Таблица 4.2.3
| Базис | х0 | х1 | х2 | х3 | х4 | х5 | х6 | Θ1 | Θ2 |
| х4 | 10 | 1 | 2 | –1 | 1 | 0 | 0 | 10 | 5 |
| х5 | 6 | 2 | 0 | 2 | 0 | 1 | 0 | 3 | – |
| х6 | 8 | –1 | 1 | 4 | 0 | 0 | 1 | – | 8 |
| Δ | 0 | 1 | 1 | –2 | 0 | 0 | 0 |
5) Выбираем минимальный параметр  в каждом столбце и отмечаем его. В данном примере отмечаем
в каждом столбце и отмечаем его. В данном примере отмечаем  и
и  (табл. 4.2.3).
(табл. 4.2.3).
6) Составляем критерий выбора вектора, вводимого в базис, и вектора, выводимого из него:  , следовательно, новый вектор, который войдёт в базис – х2, а выйдет из базиса вектор х4. Разрешающий элемент на пересечении соответствующих столбца и строки будет равен 2 (табл. 4.2.4):
, следовательно, новый вектор, который войдёт в базис – х2, а выйдет из базиса вектор х4. Разрешающий элемент на пересечении соответствующих столбца и строки будет равен 2 (табл. 4.2.4):
Таблица 4.2.4

7) Далее применяем элементарные преобразования Жордана-Гаусса и приводим выбранный столбец (  ) к базисному виду. Проведённые расчёты представлены в табл. 4.2.5 (вспомогательный параметр
) к базисному виду. Проведённые расчёты представлены в табл. 4.2.5 (вспомогательный параметр 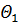 в расчётах не участвует):
в расчётах не участвует):
Таблица 4.2.5

8) После выполнения преобразований симплексная таблица будет выглядеть следующим образом (табл. 4.2.6).
Таблица 4.2.6

9) Далее продолжаем решение с нахождения признаков оптимальности решения (в данном примере  ) и рассчитываем вспомогательные параметры для найденной оценки (
) и рассчитываем вспомогательные параметры для найденной оценки (  ). Заносим их в симплексную таблицу (табл. 4.2.6), и выбираем наименьший вспомогательный параметр
). Заносим их в симплексную таблицу (табл. 4.2.6), и выбираем наименьший вспомогательный параметр  . Критерий выбора вектора составлять не нужно, т.к. у нас только один столбец
. Критерий выбора вектора составлять не нужно, т.к. у нас только один столбец 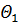 , следовательно, новым базисным вектором будет
, следовательно, новым базисным вектором будет 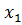 , и он заменит собой вектор
, и он заменит собой вектор  (табл. 4.2.6). Разрешающий элемент на пересечении выбранных столбца и строки равен 2. Применяем элементарные преобразования Жордана-Гаусса и приводим выбранный столбец (
(табл. 4.2.6). Разрешающий элемент на пересечении выбранных столбца и строки равен 2. Применяем элементарные преобразования Жордана-Гаусса и приводим выбранный столбец (  ) к базисному виду. Проведённые расчёты представлены в табл. 4.2.7:
) к базисному виду. Проведённые расчёты представлены в табл. 4.2.7:
Таблица 4.2.7

10) После проведённых расчётов симплексная таблица будет выглядеть следующим образом (табл. 4.2.8). Все оценки разложения векторов Δi<0, что соответствует условию задачи (минимуму) и говорит о том, что найденное решение единственное, следовательно, найденное решение является оптимальным. Выписываем ответ из соответствующих ячеек симплексной таблицы, не включая в него дополнительные переменные (х4, х5 и х6).
Таблица 4.2.8
| Базис | х0 | х1 | х2 | х3 | х4 | х5 | х6 | Θ1 | Θ2 |
| х4 | 10 | 1 | 2 | –1 | 1 | 0 | 0 | 10 | 5 |
| х5 | 6 | 2 | 0 | 2 | 0 | 1 | 0 | 3 | – |
| х6 | 8 | –1 | 1 | 4 | 0 | 0 | 1 | – | 8 |
| Δ | 0 | 1 | 1 | –2 | 0 | 0 | 0 | Θ1 | |
| х2 | 5 | 0,5 | 1 | –0,5 | 0,5 | 0 | 0 | 10 | |
| х5 | 6 | 2 | 0 | 2 | 0 | 1 | 0 | 3 | |
| х6 | 3 | –1,5 | 0 | 4,5 | –0,5 | 0 | 1 | – | |
| Δ | –5 | 0,5 | 0 | –1,5 | –0,5 | 0 | 0 | ||
| х2 | 3,5 | 0 | 1 | –1 | 0,5 | –0,25 | 0 | ||
| х1 | 3 | 1 | 0 | 1 | 0 | 0,5 | 0 | ||
| х6 | 7,5 | 0 | 0 | 6 | –0,5 | 0,75 | 1 | ||
| Δ | –6,5 | 0 | 0 | –2 | –0,5 | –0,25 | 0 |
Ответ: 
4.3. Задача линейного программирования с неограниченной целевой функцией
ПРИМЕР № 1: 

Решение:
1) Представляем данную задачу в канонической форме. Для этого во все неравенства вида «≤» добавляем дополнительные переменные с нумерацией в порядке возрастания и вносим их в целевую функцию с нулевыми коэффициентами (рис. 4.3.1):

Рисунок 4.3.1
После этих действий исходная задача будет представлена в канонической форме записи:


2) Составляем симплексную таблицу. В столбец «Базис» вписываем базисные векторы из системы ограничений (х4, х5 и х6) и заполняем таблицу коэффициентами векторов из системы ограничений (табл. 4.3.1):
Таблица 4.3.1
| Базис | х0 | х1 | х2 | х3 | х4 | х5 | х6 |
| х4 | 2 | –2 | 1 | 1 | 1 | 0 | 0 |
| х5 | 3 | –1 | 1 | 3 | 0 | 1 | 0 |
| х6 | 1 | 1 | –3 | 1 | 0 | 0 | 1 |
3) Вычисляем оценки разложений векторов системы ограничений по базису:





Далее вносим вычисленные оценки в симплексную таблицу. В данном примере задача решается на максимум, поэтому помечаем отрицательные оценки векторов (х1, х2 и х3). Для найденных оценок вычисляем вспомогательные параметры и заносим их в симплексную таблицу (табл. 4.3.2):
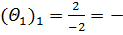
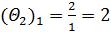







Таблица 4.3.2

4) Выбираем минимальный параметр  в каждом столбце и отмечаем его. В данном примере отмечаем
в каждом столбце и отмечаем его. В данном примере отмечаем  ,
,  и
и  (табл. 4.3.2). Составляем критерий выбора вектора, вводимого в базис, и вектора, выводимого из него:
(табл. 4.3.2). Составляем критерий выбора вектора, вводимого в базис, и вектора, выводимого из него:
 , следовательно, новый вектор, который войдёт в базис – х2, а выйдет из базиса вектор х4. Разрешающий элемент на пересечении соответствующих столбца и строки будет равен 1 (табл. 4.3.2).
, следовательно, новый вектор, который войдёт в базис – х2, а выйдет из базиса вектор х4. Разрешающий элемент на пересечении соответствующих столбца и строки будет равен 1 (табл. 4.3.2).
5) Далее применяем элементарные преобразования Жордана-Гаусса и приводим выбранный столбец (  ) к базисному виду. Проведённые расчёты представлены в табл. 4.3.3 (вспомогательный параметр
) к базисному виду. Проведённые расчёты представлены в табл. 4.3.3 (вспомогательный параметр 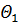 в расчётах не участвует):
в расчётах не участвует):
Таблица 4.3.3

6) После выполнения преобразований симплексная таблица будет выглядеть следующим образом (табл. 4.3.4).
Таблица 4.3.4

7) Далее продолжаем решение с нахождения признаков оптимальности решения (в данном примере 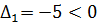 ) и рассчитываем вспомогательные параметры для найденной оценки (
) и рассчитываем вспомогательные параметры для найденной оценки (  ). Заносим их в симплексную таблицу (табл. 4.3.4), и выбираем наименьший вспомогательный параметр
). Заносим их в симплексную таблицу (табл. 4.3.4), и выбираем наименьший вспомогательный параметр  . Критерий выбора вектора составлять не нужно, т.к. у нас только один столбец
. Критерий выбора вектора составлять не нужно, т.к. у нас только один столбец 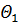 , следовательно, новым базисным вектором будет
, следовательно, новым базисным вектором будет  , и он заменит собой вектор
, и он заменит собой вектор  (табл. 4.3.4). Разрешающий элемент на пересечении выбранных столбца и строки равен 1. Применяем элементарные преобразования Жордана-Гаусса и приводим выбранный столбец (
(табл. 4.3.4). Разрешающий элемент на пересечении выбранных столбца и строки равен 1. Применяем элементарные преобразования Жордана-Гаусса и приводим выбранный столбец (  ) к базисному виду. Проведённые расчёты представлены в табл. 4.3.5:
) к базисному виду. Проведённые расчёты представлены в табл. 4.3.5:
Таблица 4.3.5

8) После проведённых расчётов симплексная таблица будет выглядеть следующим образом (табл. 4.3.6). Оценка Δ4<0, что не соответствует условию задачи (максимуму) и говорит о том, что найденное решение не оптимально, но все вспомогательные параметры для этой оценки отрицательны (  ). Следовательно, продолжить решение невозможно, и это говорит о том, что целевая функция не ограничена.
). Следовательно, продолжить решение невозможно, и это говорит о том, что целевая функция не ограничена.
Таблица 4.3.6
| Базис | х0 | х1 | х2 | х3 | х4 | х5 | х6 | Θ1 | Θ2 | Θ 3 |
| х4 | 2 | –2 | 1 | 1 | 1 | 0 | 0 | – | 2 | 2 |
| х5 | 3 | –1 | 1 | 3 | 0 | 1 | 0 | – | 3 | 1 |
| х6 | 1 | 1 | –3 | 1 | 0 | 0 | 1 | 1 | – | 1 |
| Δ | 0 | –1 | –2 | –1 | 0 | 0 | 0 | Θ1 | ||
| х2 | 2 | –2 | 1 | 1 | 1 | 0 | 0 | – | ||
| х5 | 1 | 1 | 0 | 2 | –1 | 1 | 0 | 1 | ||
| х6 | 7 | –5 | 0 | 4 | 3 | 0 | 1 | – | ||
| Δ | 4 | –5 | 0 | 1 | 2 | 0 | 0 | Θ 4 | ||
| х2 | 4 | 0 | 1 | 5 | –1 | 2 | 0 | – | ||
| х 1 | 1 | 1 | 0 | 2 | –1 | 1 | 0 | – | ||
| х6 | 12 | 0 | 0 | 14 | –2 | 5 | 1 | – | ||
| Δ | 9 | 0 | 0 | 11 | –3 | 5 | 0 |
Ответ: 
4.4. Задача линейного программирования с двумя оптимальными решениями
ПРИМЕР № 1: 

Решение:
1) Представляем задачу в канонической форме:


2) Составляем симплексную таблицу (табл. 4.4.1):
Таблица 4.4.1
| Базис | х0 | х1 | х2 | х3 | х4 | х5 | х6 |
| х4 | 12 | –2 | 3 | 1 | 1 | 0 | 0 |
| х5 | 15 | 1 | 2 | 2 | 0 | 1 | 0 |
| х6 | 10 | 2 | –1 | –3 | 0 | 0 | 1 |
| Δ | 0 | –6 | –12 | –3 | 0 | 0 | 0 |
3) Данная задача решается на максимум, следовательно, отмечаем все оценки 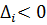 . Для найденных оценок вычисляем вспомогательные параметры и заносим их в симплексную таблицу. Выбираем минимальный параметр
. Для найденных оценок вычисляем вспомогательные параметры и заносим их в симплексную таблицу. Выбираем минимальный параметр  в каждом столбце и отмечаем его (табл. 4.4.2):
в каждом столбце и отмечаем его (табл. 4.4.2):
Таблица 4.4.2
| Базис | х0 | х1 | х2 | х3 | х4 | х5 | х6 | Θ1 | Θ2 | Θ3 |
| х4 | 12 | –2 | 3 | 1 | 1 | 0 | 0 | – | 4 | 12 |
| х5 | 15 | 1 | 2 | 2 | 0 | 1 | 0 | 15 | 7,5 | 7,5 |
| х6 | 10 | 2 | –1 | –3 | 0 | 0 | 1 | 5 | – | – |
| Δ | 0 | –6 | –12 | –3 | 0 | 0 | 0 |
4) Составляем критерий выбора вектора, вводимого в базис, и вектора, выводимого из него:  , следовательно, новый вектор, который войдёт в базис – х2, а выйдет из базиса вектор х4. Разрешающий элемент на пересечении соответствующих столбца и строки будет равен 3.
, следовательно, новый вектор, который войдёт в базис – х2, а выйдет из базиса вектор х4. Разрешающий элемент на пересечении соответствующих столбца и строки будет равен 3.
5) Далее применяем элементарные преобразования Жордана-Гаусса и приводим выбранный столбец (  ) к базисному виду. После выполнения преобразований симплексная таблица будет выглядеть следующим образом (табл. 4.4.3):
) к базисному виду. После выполнения преобразований симплексная таблица будет выглядеть следующим образом (табл. 4.4.3):
Таблица 4.4.3
| Базис | х0 | х1 | х2 | х3 | х4 | х5 | х6 | Θ1 | Θ2 | Θ3 |
| х4 | 12 | –2 | 3 | 1 | 1 | 0 | 0 | – | 4 | 12 |
| х5 | 15 | 1 | 2 | 2 | 0 | 1 | 0 | 15 | 7,5 | 7,5 |
| х6 | 10 | 2 | –1 | –3 | 0 | 0 | 1 | 5 | – | – |
| Δ | 0 | –6 | –12 | –3 | 0 | 0 | 0 | Θ1 | ||
| х2 | 4 | –2/3 | 1 | 1/3 | 1/3 | 0 | 0 | – | ||
| х5 | 7 | 7/3 | 0 | 4/3 | –2/3 | 1 | 0 | 3 | ||
| х6 | 14 | 4/3 | 0 | –8/3 | 1/3 | 0 | 1 | 10,5 | ||
| Δ | 48 | –14 | 0 | 1 | 4 | 0 | 0 | |||
| х2 | 6 | 0 | 1 | 5/7 | 1/7 | 2/7 | 0 | |||
| х1 | 3 | 1 | 0 | 4/7 | –2/7 | 3/7 | 0 | |||
| х6 | 10 | 0 | 0 | –24/7 | 5/7 | –4/7 | 1 | |||
| Δ | 90 | 0 | 0 | 9 | 0 | 6 | 0 |
6) Все оценки разложения векторов  , что соответствует условию задачи (максимуму), но говорит о том, что найденное решение не единственно возможное, следовательно, нужно продолжить решение задачи. Выписываем первое оптимальное решение в ответ и продолжаем решение (табл. 4.4.4).
, что соответствует условию задачи (максимуму), но говорит о том, что найденное решение не единственно возможное, следовательно, нужно продолжить решение задачи. Выписываем первое оптимальное решение в ответ и продолжаем решение (табл. 4.4.4).
Таблица 4.4.4
| Базис | х0 | х1 | х2 | х3 | х4 | х5 | х6 | Θ1 | Θ2 | Θ3 |
| х4 | 12 | –2 | 3 | 1 | 1 | 0 | 0 | – | 4 | 12 |
| х5 | 15 | 1 | 2 | 2 | 0 | 1 | 0 | 15 | 7,5 | 7,5 |
| х6 | 10 | 2 | –1 | –3 | 0 | 0 | 1 | 5 | – | – |
| Δ | 0 | –6 | –12 | –3 | 0 | 0 | 0 | Θ1 | ||
| х2 | 4 | –2/3 | 1 | 1/3 | 1/3 | 0 | 0 | – | ||
| х5 | 7 | 7/3 | 0 | 4/3 | –2/3 | 1 | 0 | 3 | ||
| х6 | 14 | 4/3 | 0 | –8/3 | 1/3 | 0 | 1 | 10,5 | ||
| Δ | 48 | –14 | 0 | 1 | 4 | 0 | 0 | Θ 4 | ||
| х2 | 6 | 0 | 1 | 5/7 | 1/7 | 2/7 | 0 | 42 | ||
| х1 | 3 | 1 | 0 | 4/7 | –2/7 | 3/7 | 0 | – | ||
| х6 | 10 | 0 | 0 | –24/7 | 5/7 | –4/7 | 1 | 14 | ||
| Δ | 90 | 0 | 0 | 9 | 0 | 6 | 0 | |||
| х2 | 4 | 0 | 1 | 7/5 | 0 | 6/35 | –1/5 | |||
| х1 | 7 | 1 | 0 | –4/5 | 0 | 1/5 | 2/5 | |||
| х 4 | 14 | 0 | 0 | –24/5 | 1 | –4/5 | 7/5 | |||
| Δ | 90 | 0 | 0 | 9 | 0 | 6 | 0 |
Ответ: 

4.5. Задача линейного программирования с тремя оптимальными решениями
ПРИМЕР № 1: 

Решение:
1) Представляем задачу в канонической форме:
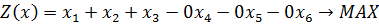

2) Составляем симплексную таблицу (табл. 4.5.1):
Таблица 4.5.1
| Базис | х0 | х1 | х2 | х3 | х4 | х5 | х6 |
| х4 | 7 | 1 | 1 | 1 | 1 | 0 | 0 |
| х5 | 9 | 2 | 1 | 3 | 0 | 1 | 0 |
| х6 | 12 | 3 | 1 | 4 | 0 | 0 | 1 |
| Δ | 0 | –1 | –1 | –1 | 0 | 0 | 0 |
3) Данная задача решается на максимум, следовательно, отмечаем все оценки 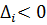 . Для найденных оценок вычисляем вспомогательные параметры и заносим их в симплексную таблицу. Выбираем минимальный параметр
. Для найденных оценок вычисляем вспомогательные параметры и заносим их в симплексную таблицу. Выбираем минимальный параметр  в каждом столбце и отмечаем его (табл. 4.5.2):
в каждом столбце и отмечаем его (табл. 4.5.2):
Таблица 4.5.2
| Базис | х0 | х1 | х2 | х3 | х4 | х5 | х6 | Θ1 | Θ2 | Θ3 |
| х4 | 7 | 1 | 1 | 1 | 1 | 0 | 0 | 7 | 7 | 7 |
| х5 | 9 | 2 | 1 | 3 | 0 | 1 | 0 | 4,5 | 9 | 3 |
| х6 | 12 | 3 | 1 | 4 | 0 | 0 | 1 | 4 | 12 | 3 |
| Δ | 0 | –1 | –1 | –1 | 0 | 0 | 0 |
4) Составляем критерий выбора вектора, вводимого в базис, и вектора, выводимого из него:  , следовательно, новый вектор, который войдёт в базис – х2, а выйдет из базиса вектор х4. Разрешающий элемент на пересечении соответствующих столбца и строки будет равен 1.
, следовательно, новый вектор, который войдёт в базис – х2, а выйдет из базиса вектор х4. Разрешающий элемент на пересечении соответствующих столбца и строки будет равен 1.
5) Далее применяем элементарные преобразования Жордана-Гаусса и приводим выбранный столбец (  ) к базисному виду. После выполнения преобразований симплексная таблица будет выглядеть следующим образом (табл. 4.5.3):
) к базисному виду. После выполнения преобразований симплексная таблица будет выглядеть следующим образом (табл. 4.5.3):
Таблица 4.5.3
| Базис | х0 | х1 | х2 | х3 | х4 | х5 | х6 | Θ1 | Θ2 | Θ3 |
| х4 | 7 | 1 | 1 | 1 | 1 | 0 | 0 | 7 | 7 | 7 |
| х5 | 9 | 2 | 1 | 3 | 0 | 1 | 0 | 4,5 | 9 | 3 |
| х6 | 12 | 3 | 1 | 4 | 0 | 0 | 1 | 4 | 12 | 3 |
| Δ | 0 | –1 | –1 | –1 | 0 | 0 | 0 | Θ1 | Θ3 | |
| х2 | 7 | 1 | 1 | 1 | 1 | 0 | 0 | 7 | 7 | |
| х5 | 2 | 1 | 0 | 2 | –1 | 1 | 0 | 2 | 1 | |
| х6 | 5 | 2 | 0 | 3 | –1 | 0 | 1 | 2,5 | 5/3 | |
| Δ | 7 | 0 | 0 | 0 | 1 | 0 | 0 |
6) Все оценки разложения векторов  , что соответствует условию задачи (максимуму), но говорит о том, что найденное решение не единственно возможное, следовательно, нужно продолжить решение задачи. Выписываем первое оптимальное решение в ответ и продолжаем решение (табл. 4.5.4).
, что соответствует условию задачи (максимуму), но говорит о том, что найденное решение не единственно возможное, следовательно, нужно продолжить решение задачи. Выписываем первое оптимальное решение в ответ и продолжаем решение (табл. 4.5.4).
Таблица 4.5.4
| Базис | х0 | х1 | х2 | х3 | х4 | х5 | х6 | Θ1 | Θ2 | Θ3 |
| х4 | 7 | 1 | 1 | 1 | 1 | 0 | 0 | 7 | 7 | 7 |
| х5 | 9 | 2 | 1 | 3 | 0 | 1 | 0 | 4,5 | 9 | 3 |
| х6 | 12 | 3 | 1 | 4 | 0 | 0 | 1 | 4 | 12 | 3 |
| Δ | 0 | –1 | –1 | –1 | 0 | 0 | 0 | Θ1 | Θ3 | |
| х2 | 7 | 1 | 1 | 1 | 1 | 0 | 0 | 7 | 7 | |
| х5 | 2 | 1 | 0 | 2 | –1 | 1 | 0 | 2 | 1 | |
| х6 | 5 | 2 | 0 | 3 | –1 | 0 | 1 | 2,5 | 5/3 | |
| Δ | 7 | 0 | 0 | 0 | 1 | 0 | 0 | Θ3 | ||
| х2 | 5 | 0 | 1 | –1 | 2 | –1 | 0 | – | ||
| х1 | 2 | 1 | 0 | 2 | –1 | 1 | 0 | 1 | ||
| х6 | 1 | 0 | 0 | –1 | 1 | –2 | 1 | – | ||
| Δ | 7 | 0 | 0 | 0 | 1 | 0 | 0 | |||
| х2 | 6 | 0,5 | 1 | 0 | 1,5 | –0,5 | 0 | |||
| х3 | 1 | 0,5 | 0 | 1 | –0,5 | 0,5 | 0 | |||
| х6 | 2 | 0,5 | 0 | 0 | 0,5 | 1,5 | 1 | |||
| Δ | 7 | 0 | 0 | 0 | 1 | 0 | 0 |
Ответ:


4.6. Задачи для самостоятельного решения
1) Производственный цех выпускает три вида деталей, которые проходят обработку на двух станках. На рис. 4.6.1 показана технологическая схема обработки деталей каждого вида с указанием времени их обработки на станках. Суточный ресурс рабочего времени первого станка составляет 22 машино-часа, второго станка – 21 машино-час. Стоимость детали первого вида – 300 у.е., второго вида – 100 у.е., третьего вида – 200 у.е. соответственно. Требуется составить суточный план обработки деталей с целью максимизации прибыли с учётом заказа размером 50 шт. деталей второго вида.[5]

Рисунок 4.6.1. Схема обработки деталей.
Математическая модель задачи имеет вид:

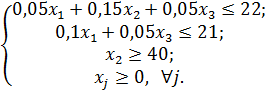
Ответ: Максимальная суточная прибыль при данных условиях составит 76000 у.е. при обработке 130 шт. деталей № 1, 50 шт. деталей № 2 и 160 шт. деталей № 3, т.е. 
2) На заводе изготавливается продукция двух артикулов. Эти виды продукции изготавливаются на двух станках – новом и б/у. В табл. 4.6.1 указаны производительности станков при изготовлении каждого вида продукции, суммарные производительные мощности станков в расчёте на 1 рабочий месяц, трудовые затраты на обслуживание станков в часах рабочего времени на 1 час работы станка, цены на единицу продукции каждого вида. Требуется составить месячный план выпуска продукции с целью максимизации прибыли при условии, что продукции Артикула №1 должно быть изготовлено не менее 500 шт. (т.к. под выпуск этой продукции уже внесена предоплата).[6]
Таблица 4.6.1
| Тип станка | Мощности станков, ч | Трудозатраты на обслуживание станков, ч | Производительность станка, шт/ч | |
| Артикул 1 | Артикул 2 | |||
| 1 | 710 | 0,05 | 20 | 15 |
| 2 | 680 | 0,1 | 12 | 10 |
| Цена единицы продукции, у.е. | 18 | 25 | ||
Математическая модель задачи имеет вид:


Ответ: Максимальная прибыль при данных условиях составит 428750 у.е. при изготовлении продукции Артикула №1 в течение 500 ч. на станке № 1, а продукции Артикула № 2 в течение 210 ч. на станке № 1 и в течение 680 ч. на станке № 2, т.е. 
3) 

Ответ: 
4) 

Ответ: 

5) 

Ответ: 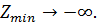
6) 

Ответ: 
7) 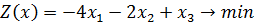

Ответ: 

8) 

Ответ: 
9) 
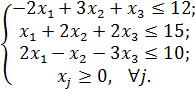
Ответ: 

10) 

Ответ: 
11) 
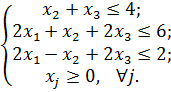
Ответ: 
12) 

Ответ: 
13) 
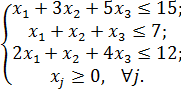
Ответ: 
14) 

Ответ: 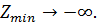
15) 

Ответ: 
5. Метод искусственного базиса (М-метод)
Метод искусственного базиса является симплексным методом решения задач линейного программирования в случае, когда задача не имеет начального опорного решения ввиду отсутствия базиса (даже после введения дополнительных векторов). Для решения задачи составляется расширенная задача с помощью введения искусственных переменных.[1]
Искусственными переменными называются неотрицательные переменные, которые вводятся в ограничения-равенства для получения начального опорного решения с базисом из единичных векторов. Каждая искусственная переменная вводится в левую часть одного из уравнений системы ограничений с коэффициентом « +1 » и в целевую функцию в задаче на максимум с коэффициентом « – М », а в задаче на минимум с коэффициентом « + М ». Сам коэффициент «М»→+∞ и имеет смысл «штрафа» (mulct) за ввод искусственных переменных, чтобы в оптимальном решении полученной задачи значение этой переменной было равно нулю.
Алгоритм решения задач линейного программирования методом искусственного базиса рассмотрим на следующих примерах.
Дата добавления: 2020-11-15; просмотров: 140; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
