Пример. При каких значениях x справедливо нер-во
Иррациональные уравнения
Ранее мы рассматривали целые и дробно-рациональные уравнения. В них выражение с переменной НЕ могло находиться под знаком радикала, а также возводиться в дробную степень. Если же переменная оказывается под радикалом, то получается иррациональное уравнение.

Приведем примеры иррациональных ур-ний:

Заметим, что не всякое уравнение, содержащее радикалы, является иррациональным. В качестве примера можно привести
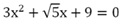
Это не иррациональное, а всего лишь квадратное ур-ние. Дело в том, что под знаком радикала стоит только число 5, а переменных там нет.
Простейшие иррациональные уравнения
Начнем рассматривать способы решения иррациональных уравнений. В простейшем случае в нем справа записано число, а вся левая часть находится под знаком радикала. Выглядит подобное ур-ние так:
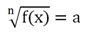
где а – некоторое число (константа), f(x) – рациональное выражение.
Для его решения необходимо обе части возвести в степень n, тогда корень исчезнет:
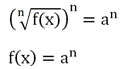
Получаем рациональное ур-ние, решать которые мы уже умеем. Однако есть важное ограничение. Мы помним, что корень четной степени всегда равен положительному числу, и его нельзя извлекать из отрицательного числа. Поэтому, если в ур-нии
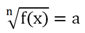
n – четное число, то необходимо, чтобы а было положительным. Если же оно отрицательное, то ур-ние не имеет корней. Но на нечетные n такое ограничение не распространяется.
|
|
|
Пример. Решите ур-ние
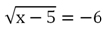
Решение. Справа стоит отрицательное число (– 6), но квадратный корень (если быть точными, то арифметический квадратный корень) не может быть отрицательным. Поэтому ур-ние корней не имеет.
Ответ: корней нет.
Пример. Решите ур-ние
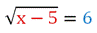
Решение. Теперь справа стоит положительное число, значит, мы имеем право возвести обе части в квадрат. При этом корень слева исчезнет:
x– 5 = 62
х = 36 + 5
х = 41
Ответ: 41.
Пример. Решите ур-ние
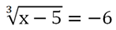
Решение. Справа стоит отрицательное число, но это не является проблемой, ведь кубический корень может быть отрицательным. Возведем обе части в куб:
х – 5 = (– 6)3
х = – 216 + 5
х = – 211
Ответ: – 211.
Конечно, под знаком корня может стоять и более сложное выражение, чем (х – 5).
Пример. Найдите решение ур-ния
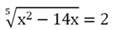
Решение. Возведем обе части в пятую степень:
х2 – 14х = 25
х2 – 14х – 32 = 0
Получили квадратное ур-ние, которое можно решить с помощью дискриминанта:
D = b2– 4ac = (– 14)2 – 4•1•(– 32) = 196 + 128 = 324
х1 = (14 – 18)/2 = – 2
х2 = (14 + 18)/2 = 16
Итак, нашли два корня: (– 2) и 16.
Ответ: (– 2); 16.
Несколько более сложным является случай, когда справа стоит не постоянное число, а какое-то выражение с переменной g(x). Алгоритм решения тот же самый – необходимо возвести в степень ур-ние, чтобы избавиться от корня. Но, если степень корня четная, то необходимо проверить, что полученные корни ур-ния не обращают правую часть, то есть g(x), в отрицательное число. В противном случае их надо отбросить как посторонние корни.
|
|
|
Пример. Решите ур-ние

Решение. Возводим обе части во вторую степень:
х – 2 = (х – 4)2
х – 2 = х2 – 8х + 16
х2 – 9х + 18 = 0
D = b2– 4ac = (– 9)2 – 4•1•18 = 81 – 72 = 9
х1 = (9 – 3)/2 = 3
х2 = (9 + 3)/2 = 6
Получили два корня, 3 и 6. Теперь проверим, во что они обращают правую часть исходного ур-ния (х – 4):
при х = 3 х – 4 = 3 – 4 = – 1
при х = 6 6 – 4 = 6 – 4 = 2
Корень х = 3 придется отбросить, так как он обратил правую часть в отрицательное число. В результате остается только х = 6.
Ответ: 6.
Пример. Решите ур-ние

Решение. Здесь используется кубический корень, а потому возведем обе части в куб:
3х2 + 6х – 25 = (1 – х)3
3х2 + 6х – 25 = 1 – 3х + 3х2 – х3
х3 + 9х – 26 = 0
Получили кубическое ур-ние. Решить его можно методом подбора корня. Из всех делителей свободного коэффициента (– 26) только двойка обращает ур-ние в верное равенство:
23 + 9•2 – 26 = 0
8 + 18 – 26 = 0
0 = 0
Других корней нет. Это следует из того факта, что функция у = х3 + 9х – 26 является монотонной.
Заметим, что если подставить х = 2 в левую часть исходного ур-ния 1 – х, то получится отрицательное число:
|
|
|
при х = 2 1 – х = 1 – 2 = – 1
Но означает ли это, что число 2 НЕ является корнем? Нет, ведь кубический корень вполне может быть и отрицательным (в отличие от квадратного). На всякий случай убедимся, что двойка – это действительно корень исходного уравнения:

Ответ: 2.
Уравнения с двумя квадратными корнями
Ситуация осложняется, если в ур-нии есть сразу два квадратных корня. В этом случае их приходится убирать последовательно. Сначала мы переносим слагаемые через знак «=» таким образом, чтобы слева остался один из радикалов и ничего, кроме него. Возводя в квадрат такое ур-ние, мы избавимся от одного радикала, после чего мы получим более простое ур-ние. После получения всех корней надо проверить, какие из них являются посторонними. Для этого их надо просто подставить в исходное ур-ние.
Пример. Решите ур-ние
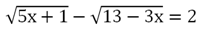
Решение. Перенесем вправо один из корней:
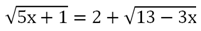
Возведем обе части в квадрат. Обратите внимание, что левый корень при этом исчезнет, а правый – сохранится:

Теперь снова перемещаем слагаемые так, чтобы в одной из частей не осталось ничего, кроме корня:

Поделим на 4:
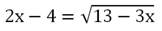
Снова возведем ур-ние в квадрат, чтобы избавиться и от второго корня:
|
|
|
(2х – 4)2 = 13 – 3х
4х2 – 16х + 16 = 13 – 3х
4х2 – 13х + 3 = 0
D = b2– 4ac = (– 13)2 – 4•4•3 = 169 –48 = 121
х1 = (13 – 11)/8 = 0,25
х2 = (13 + 11)/8 = 3
Имеем два корня: 3 и 0,25. Но вдруг среди них есть посторонние? Для проверки подставим их в исходное ур-ние. При х = 0,25 имеем:

Получилось ошибочное равенство, а это значит, что 0,25 не является корнем ур-ния. Далее проверим х = 3
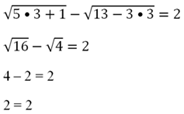
На этот раз получилось справедливое равенство. Значит, тройка является корнем ур-ния.
Ответ: 3
Введение новых переменных
Предложенный метод последовательного исключения радикалов плохо работает в том случае, если корни не квадратные, а имеют другую степень. Рассмотрим ур-ние
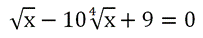
Последовательно исключить корни, как в предыдущем примере, здесь не получится (попробуйте это сделать самостоятельно). Однако помочь может замена переменной.
Для начала перепишем ур-ние в более удобной форме, когда вместо корней используются степени:
х1/2 – 10х1/4 + 9 = 0
Теперь введем переменную t = x1/4. Тогда х1/2 = (х1/4)2 = t2. Исходное ур-ние примет вид
t2– 10t + 9 = 0
Это квадратное ур-ние. Найдем его корни:
D = b2– 4ac = (– 10)2 – 4•1•9 = 100 – 36 = 64
t1 = (10 – 8)/2 = 1
t2 = (10 + 8)/2 = 9
Получили два значения t. Произведем обратную замену:
х1/4 = 1 или х1/4 = 9
Возведем оба ур-ния в четвертую степень:
(х1/4)4 = 14 или (х1/4)4 = 34
х = 1 или х = 6561
Полученные числа необходимо подставить в исходное ур-ние и убедиться, что они не являются посторонними корнями:
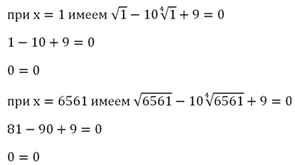
В обоих случаях мы получили верное равенство 0 = 0, а потому оба числа, 1 и 6561, являются корнями ур-ния.
Пример. Решите ур-ние
х1/3 + 5х1/6 – 24 = 0
Решение. Произведем замену t = x1/6, тогда х1/3 = (х1/6)2 = t2. Исходное ур-ние примет вид:
t2 + 5t – 24 = 0
Его корни вычислим через дискриминант:
D = b2– 4ac = 52 – 4•1•(– 24) = 25 + 96 = 121
t1 = (– 5 – 11)/2 = – 8
t2 = (– 5 + 11)/2 = 3
Далее проводим обратную заменуx1/6 = t:
х1/6 = – 8 или х1/6 = 3
Первое ур-ние решений не имеет, а единственным решением второго ур-ния является х = 36 = 729. Если подставить это число в исходное ур-ние, то можно убедиться, что это не посторонний корень.
Ответ: 729.
Замена иррационального уравнения системой
Иногда для избавления от радикалов можно вместо них ввести дополнительные переменные и вместо одного иррационального ур-ния получить сразу несколько целых, которые образуют систему. Это один из самых эффективных методов решения иррациональных уравнений.
Пример. Решите ур-ние
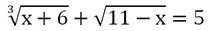
Решение. Заменим первый корень буквой u, а второй – буквой v:
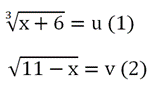
Исходное ур-ние примет вид
u + v = 5 (3)
Если возвести (1) и (2) в куб и квадрат соответственно (чтобы избавиться от корней), то получим:
х + 6 = u3 (4)
11 – х = v2 (5)
Ур-ния (3), (4) и (5) образуют систему с тремя неизвестными, в которой уже нет радикалов:
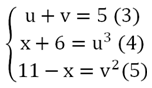
Попытаемся ее решить. Сначала сложим (4) и (5), ведь это позволит избавиться от переменной х:
(х + 6) + (11 – х) = u3 + v2
17 = u3 + v2 (6)
из (3) можно получить, что v = 5 – u. Подставим это в (6) вместо v:
17 = u3 + v2 (6)
17 = u3 + (5 – u)2
17 = u3 + u2– 10u + 25
u3 + u2 – 10u + 8 = 0
Получили кубическое ур-ние. Мы уже умеем решать их, подбирая корни. Не вдаваясь в подробности решения, укажем, что корнями этого ур-ния являются числа
u1 = 1; u2 = 2; u3 = – 4
подставим полученные значения в (4):
x + 6 = u3 (5)
x + 6 = 13или х + 6 = 23 или х + 6 = (– 4)3
x + 6 = 1или х + 6 = 8 или х + 6 = – 64
х = – 5 или х = 2 или х = – 70
Итак, нашли три возможных значения х. Но, конечно же, среди них могут оказаться посторонние корни. Поэтому нужна проверка – подставим полученные результаты в исходное ур-ние. При х = – 5 получим
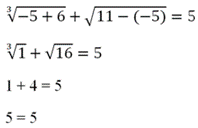
Корень подошел. Проверяем следующее число, х = 2:

Корень снова оказался верным. Осталась последняя проверка, для х = – 70:
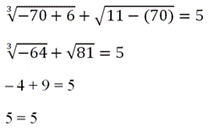
Итак, все три числа прошли проверку.
Ответ: (– 5); 2; (– 70).
Уравнения с «вложенными» радикалами
Порою в ур-нии под знаком радикала стоит ещё один радикал. В качестве примера приведем такую задачу:

При их решении следует сначала избавиться от «внешнего радикала», после чего можно будет заняться и внутренним. То есть в данном случае надо сначала возвести обе части равенства в квадрат:

Внешний радикал исчез. Теперь будем переносить слагаемые, чтобы в одной из частей остался только радикал:
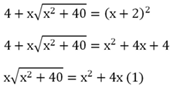
Хочется поделить полученное ур-ние (1) на х, однако важно помнить, что деление на ноль запрещено. То есть, если мы делим на х, то мы должны наложить дополнительное ограничение х ≠ 0. Случай же, когда х всё же равен нулю, мы рассматриваем отдельно. Для этого подставим х = 0 сразу в исходное ур-ние:
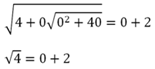
Получили верное рав-во, значит, 0 является корнем. Теперь возвращаемся к (1) и делим его на х:
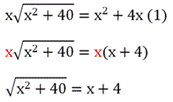
Возводим в квадрат и получаем:
х2 + 40 = (х + 4)2
х2 + 40 = х2 + 8х + 16
8х = 24
х = 3
И снова нелишней будет проверка полученного корня:
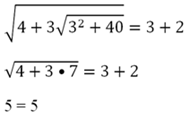
Корень подошел.
Ответ: 0; 3.
Иррациональные неравенства
По аналогии с иррациональными ур-ниями иррациональными неравенствами называют такие нер-ва, в которых выражение с переменной находится под знаком радикала или возводится в дробную степень. Приведем примеры иррациональных нер-в:
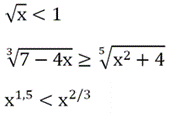
Нет смысла решать иррациональные нер-ва, если есть проблемы с более простыми, то есть рациональными нер-вами, а также с их системами. Поэтому на всякий случай ещё раз просмотрите этот и ещё вот этот уроки.
Начнем с решения иррациональных неравенств простейшего вида, у которых в одной из частей стоит выражение под корнем, а в другой – постоянное число. Достаточно очевидно, что нер-во вида
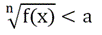
Может быть справедливым только тогда, когда

То есть, грубо говоря, нер-ва можно возводить в степень. Однако при этом могут возникнуть посторонние решения. Дело в том, что нужно учитывать и тот факт, что подкоренное выражение должно быть неотрицательным в том случае, если степень корня является четной. Таким образом, нер-во
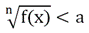
при четном n можно заменить системой нер-в

Пример. При каких значениях x справедливо нер-во
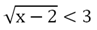
Решение. С одной стороны, при возведении нер-ва в квадрат мы получим такое нер-во:
х – 2 < 9
х < 11
Однако подкоренное выражение должно быть неотрицательным, то есть
х – 2 ⩾ 0
x⩾2
Итак, мы получили, что 2 ⩽ х < 11. Напомним, что традиционно решения нер-в записывают с помощью промежутков. Поэтому двойное нер-во 2 ⩽ х < 11 мы заменим на равносильную ему запись х∈[2; 11).
Ответ: х∈[2; 11).
Пример. Решите нер-во
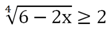
Решение. Возведем нер-во в четвертую степень:
6 – 2х ⩾ 24
6 – 2х ⩾ 16 (1)
– 2х ⩾ 10
х ⩽ – 5 (знак нер-ва изменился из-за того, что мы поделили его на отрицательное число)
Получили промежуток х∈(– ∞; – 5). Казалось бы, надо записать ещё одно нер-во
6 – 2х ⩾ 0 (2)
чтобы подкоренное выражение было неотрицательным. Однако сравните (1) и (2). Ясно, что если (1) выполняется, то справедливым будет и (2), ведь если какое-то выражение больше или равно двум, то оно автоматически будет и больше нуля! Поэтому (2) можно и не решать.
Ответ: х∈(– ∞; – 5)
Теперь посмотрим на простейшие нер-ва с корнем нечетной степени.
Дата добавления: 2020-11-15; просмотров: 73; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
