Доказательство формул Крамера
Запишем матричное равенство 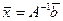 , учитывая структуру обратной матрицы:
, учитывая структуру обратной матрицы:
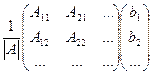 тогда
тогда 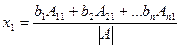 как видим, алгебраические дополнения здесь именно к элементам 1-го столбца, и умножаются они на
как видим, алгебраические дополнения здесь именно к элементам 1-го столбца, и умножаются они на  , то есть, как если бы вместо 1-го столбца была поставлена правая часть системы.
, то есть, как если бы вместо 1-го столбца была поставлена правая часть системы.
Эти два способа используются чаще для матриц 2 и 3 порядка, т.к. они очень трудоёмкие, если матрица порядка 4 и больше.
Задача 53 (А,Б). Решить систему уравнений матричным методом и методом Крамера. 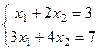 .
.
Решение. А) Матричный вид системы: 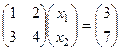 , обратную матрицу для этой матрицы ранее находили, это
, обратную матрицу для этой матрицы ранее находили, это  . Тогда
. Тогда 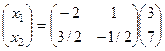 =
=  . Итак,
. Итак, 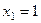 ,
, 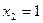 .
.
Б) 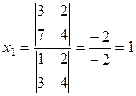 ,
, 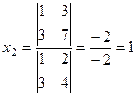 .
.
Ответ. 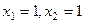 .
.
Задача 54. Решить систему линейных уравнений 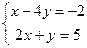 .
.
Решение. А. Матричным методом.
Запишем систему в виде: 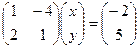 .
.
Найдём обратную матрицу для А.
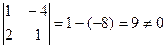 .
.

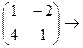
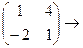
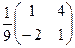
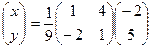 =
= 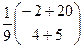 =
= 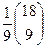 =
=  .
.
Б. Методом Крамера.
 =
= 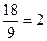
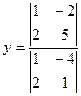 =
= 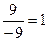 .
.
Ответ. 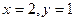 .
.
Метод Гаусса.
Задача 55. 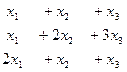
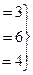
Решение. Преобразования расширенной матрицы:
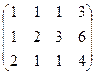
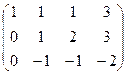
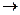
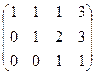 .
.
Сначала из 2-й строки вычли 1-ю, а из 3-й удвоенную 1-ю.
На втором этапе, к 3-й прибавили 2-ю.
Система после преобразований:
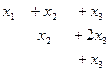
 , из последнего
, из последнего  = 1, подставляем в предпоследнее, будет
= 1, подставляем в предпоследнее, будет 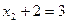 , то есть
, то есть  =1. Далее, уже известные
=1. Далее, уже известные 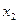 и
и 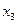 подставми в первое уравнение, и получим
подставми в первое уравнение, и получим  =1.
=1.
Ответ. 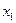 =1,
=1, 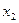 =1,
=1,  = 1, или
= 1, или 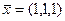 .
.
Задача 56. Решить систему уравнений 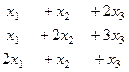
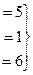
Решение. Построим расширенную матрицу и преобразуем её.
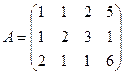
чтобы обнулились коэффициенты ниже левого верхнего угла, то есть чтобы исчезла переменная 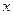 из всех уравнений кроме первого, надо:
из всех уравнений кроме первого, надо:
|
|
|
а) из 2-й строки вычесть 1-ю;
б) из 3-й строки вычесть удвоенную 1-ю.

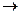
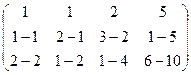 =
= 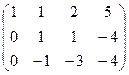
Теперь, чтобы обнулить ниже чем  , нужно к 3-й строке просто прибавить 2-ю, так как знаки там противоположны. При этом структуру из нулей, которые уже получились слева, мы на последующем шаге всё равно никак не испортим, ведь там к 0 будет прибавляться 0 либо вычитаться 0, то есть ступенчатая структура там уже всё равно будет сохраняться.
, нужно к 3-й строке просто прибавить 2-ю, так как знаки там противоположны. При этом структуру из нулей, которые уже получились слева, мы на последующем шаге всё равно никак не испортим, ведь там к 0 будет прибавляться 0 либо вычитаться 0, то есть ступенчатая структура там уже всё равно будет сохраняться.
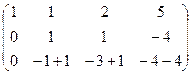 =
= 
Когда в основной матрице уже получена треугольная структура, снова перепишем в виде системы
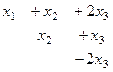
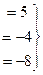 В первом уравнении 3 неизвестных, а в каждом следующем всё меньше и меньше, а в последнем вообще только одна неизвестная. Именно этой цели мы и хотели добиться, приводя к треугольному виду: из последнего уравнения можно теперь сразу выразить
В первом уравнении 3 неизвестных, а в каждом следующем всё меньше и меньше, а в последнем вообще только одна неизвестная. Именно этой цели мы и хотели добиться, приводя к треугольному виду: из последнего уравнения можно теперь сразу выразить 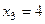 . Затем с этой информацией мы поднимаемся в предпоследнее уравнение, где две неизвестных, впрочем, одна из них уже известна.
. Затем с этой информацией мы поднимаемся в предпоследнее уравнение, где две неизвестных, впрочем, одна из них уже известна.

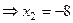 .
.
А теперь уже две последних неизвестных стали известны, и с этой информацией поднимаемся в 1-е уравнение, 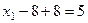
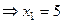 .
.
Ответ. 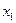 =5,
=5, 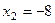 ,
, 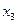 =4.
=4.
Можно ответ записать и в виде вектора: 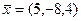 .
.
Задача домашняя. Решить систему уравнений 
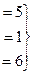
(как в прошлой, но у элемента 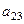 изменили знак).
изменили знак).
|
|
|
Ответ. 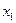 =2,
=2, 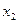 =1,
=1, 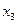 =1.
=1.
Задача 57. Решить систему уравнений 
Решение. При построении расширенной матрицы, сразу же домножим 2-е и 3-е уравнения на такие коэффициенты, чтобы в начале строки были числа, кратные угловому элементу. А именно, 2-ю строку на 2, а 3-ю строку на 4. Так надо, чтобы потом в методе Гаусса можно было не домножать на дробные коэффициенты при вычитании строк.



Но в данном случае заметим, что совпадает существенная часть 1 и 3 строк, и если сразу вычесть 1-ю строку из 3-й, то можно будет тут же найти  .
.


Из 3-го уравнения теперь следует  .
.
А далее можно составить более простую систему на 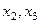 , уже с учётом
, уже с учётом 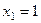 .
.

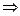
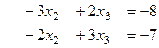
Теперь домножим, чтобы получить кратное, и приведём к треугольной структуре.
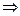
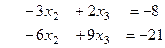
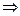

Из последнего 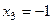 , а далее
, а далее  .
.
Ответ. 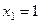 ,
, 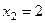 ,
, 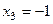 .
.
Дата добавления: 2020-11-15; просмотров: 62; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
