Анализ решения в случае различных действительных корней характеристического уравнения
Разряд конденсатора через катушку
Ниже рассматривается пример расчета переходного процесса, имеющий важное теоретическое значение.
Постановка задачи
Конденсатор ёмкостью С предварительно заряжен до напряжения  . После замыкания ключа (рис.9) конденсатор разряжается через лабораторную катушку с параметрами R и L . Требуется определить переходный ток.
. После замыкания ключа (рис.9) конденсатор разряжается через лабораторную катушку с параметрами R и L . Требуется определить переходный ток.


Рис.1.9. Разряд конденсатора через катушку
Переходный процесс описывается уравнением Кирхгофа

 (1.11)
(1.11)
Перед замыканием ключа ток в катушке отсутствовал, согласно первому закону коммутации
 (1.12)
(1.12)
Согласно второму закону коммутации напряжение на конденсаторе сохраняется неизменным в момент замыкания ключа,
 (1.13)
(1.13)
Замечание к условию (13). На рис.9 показаны положительно и отрицательно заряженные пластины конденсатора (до коммутации), направление напряжения  выбрано так, чтобы его величина была положительной
выбрано так, чтобы его величина была положительной  . Направления разрядного тока i и напряжения на конденсаторе
. Направления разрядного тока i и напряжения на конденсаторе  одинаковы, как требует соглашение о направлениях токов и напряжений на пассивных элементах (И 1.25 в первой части учебного пособия). Так как направления напряжений
одинаковы, как требует соглашение о направлениях токов и напряжений на пассивных элементах (И 1.25 в первой части учебного пособия). Так как направления напряжений  и
и  противоположны, то
противоположны, то  .
.
|
|
|
В математическую постановку задачи входят уравнение (1.11) и независимые начальные условия (1.12) и (1.13). Можно сказать, что соотношения (1.11-1.13) представляют собой математическую модель переходного процесса (разряда конденсатора через катушку).
После прекращения переходного процесса тока в цепи нет. Переходный ток имеет только свободную составляющую
 . (1.14)
. (1.14)
Здесь две экспоненциальных составляющих, потому что в цепи два реактивных элемента.
Вывод и решение характеристического уравнения
Продифференцируем уравнение (1.11) по переменной t, в результате получается дифференциальное уравнение второго порядка
 (1.15)
(1.15)
Соответствующее характеристическое уравнение имеет вид

его корни


Введем сокращенные обозначения

 (1.16)
(1.16)
В сокращенной форме записи
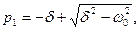
 (1.17)
(1.17)
Заметим, что  и вторая экспонента убывает с течением времени быстрее первой.
и вторая экспонента убывает с течением времени быстрее первой.
Определение постоянных интегрирования
|
|
|
В выражении (1.14) для переходного тока нужно найти две постоянных интегрирования  и
и 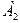 , для этого необходимо знать начальные значения тока i(0) и его производной
, для этого необходимо знать начальные значения тока i(0) и его производной  По первому закону коммутации i(0)=0. Значение
По первому закону коммутации i(0)=0. Значение  относится к зависимым начальным условиям. Чтобы найти его, запишем уравнение переходного процесса (11) для момента коммутации t =0:
относится к зависимым начальным условиям. Чтобы найти его, запишем уравнение переходного процесса (11) для момента коммутации t =0:

C учетом независимых начальных условий (1.12) и (1.13) получаем, что

следовательно,
 (1.18)
(1.18)
Теперь составим систему уравнений для определения постоянных  и
и 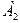 . Из выражения (1.14) для переходного тока следует, что
. Из выражения (1.14) для переходного тока следует, что
 (1.19)
(1.19)
(второе равенство выполняется вследствие начального условия (1.12) i(0)=0). Продифференцируем равенство (1.14)

и запишем его для момента времени t =0
 (1.20)
(1.20)
(второе равенство выполняется вследствие начального условия (1.18)). Решив уравнения (1.19) и (1.20), находим что


С учетом выражений (1.17) для корней характеристического уравнения получаем

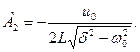 (1.21)
(1.21)
Определение переходного тока
Остается подставить в формулу (1.14) найденные ранее коэффициенты (1.21) и показатели (1.17):
|
|
|
 (1.22)
(1.22)
Здесь показатели экспонент могут принимать как действительные, так и комплексные значения.
Анализ решения в случае различных действительных корней характеристического уравнения
Корни характеристического уравнения и показатели экспонент в выражении для переходного тока являются действительными числами, если  Используя выражения (1.16) для
Используя выражения (1.16) для 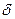 и
и  , получаем эквивалентное неравенство
, получаем эквивалентное неравенство

Это значит, что характеристическое уравнение имеет различные действительные корни, если активное сопротивление рассматриваемой цепи достаточно велико. На рис. 1.10 показан график переходного тока для этого случая.


Рис. 1.10. Апериодический разряд конденсатора через катушку, 

Переходный процесс практически прекращается за промежуток времени  ; это время затухания первой экспоненты,
; это время затухания первой экспоненты,  Вторая экспонента затухает раньше, так как
Вторая экспонента затухает раньше, так как  и
и 
| И 1.12 | При достаточно большом активном сопротивлении цепи переходный процесс носит апериодический (неколебательный) характер. |
Дата добавления: 2020-04-25; просмотров: 126; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
