Теперь вернемся к нашей дороге.
Идеально посчитанная крутизна – это куртизна, вычисленная для бесконечно малого отрезка пути, то есть:
k =  при Δx→0.
при Δx→0.
Заметим, что при бесконечно малом перемещении изменение высоты тоже будет бесконечно мало.
Но бесконечно малое – не значит равное нулю. Если поделить друг на друга бесконечно малые числа, может получиться вполне обычное число.
Например, 2. То есть одна малая величина может быть ровно в 2 раза больше другой.
К чему все это?
Дорога, крутизна… Мы ведь не в автопробег отправляемся, а математику учим.
А в математике все точно так же, только называется по-другому.
Понятие производной
Производная функции это отношение приращения функции к приращению аргумента при бесконечно малом приращение аргумента.
Приращением в математике называют изменение.
То, насколько изменился аргумент (x) при продвижении вдоль оси Ox, называется приращением аргумента и обозначается Δx.
То, насколько изменилась функция (высота) при продвижении вперед вдоль оси Ox на расстояние Δx, называется приращением функции и обозначается Δf.
Итак, производная функции f(x) – это отношение Δf к Δx при Δx→0.
Обозначаем производную той же буквой, что и функцию, только со штрихом сверху справа: f ′ ( x ) или просто f ' ′.
Итак, запишем формулу производной, используя эти обозначения:
f ′ ( x ) =  при Δx→0 при Δx→0
|
Как и в аналогии с доро́гой здесь при возрастании функции производная положительна, а при убывании – отрицательна.
|
|
|
А бывает ли производная равна нулю?
Конечно. Например, если мы едем по ровной горизонтальной дороге, крутизна равна нулю. И правда, высота ведь не совсем меняется. Так и с производной: производная постоянной функции (константы) равна нулю:
C '= 0, C = const, так как приращение такой функции равно нулю при любом Δx.
А ещё?
Давайте вспомним пример с вершиной холма. Там получалось, что можно так расположить концы отрезка по разные стороны от вершины, что высота на концах оказывается одинаковой, то есть отрезок располагается параллельно оси Ox:

Но большие отрезки – признак неточного измерения. Будем поднимать наш отрезок вверх параллельно самому себе, тогда его длина будет уменьшаться.

В конце концов, когда мы будем бесконечно близко к вершине, длина отрезка станет бесконечно малой.
Но при этом он остался параллелен оси Ox, то есть разность высот на его концах Δf равна нулю (не стремится, а именно равна).
Значит, производная
f ′(xвершины) =  =
=  = 0.
= 0.
Понять это можно так: когда мы стоим на самой вершине, меленькое смещение влево или вправо изменяет нашу высоту ничтожно мало.
|
|
|
Есть и чисто алгебраическое объяснение: левее вершины функция возрастает, а правее – убывает.
Как мы уже выяснили ранее, при возрастании функции производная положительна, а при убывании – отрицательна.
Но меняется она плавно, без скачков (т.к. дорога нигде не меняет наклон резко).
Поэтому между отрицательными и положительными значениями обязательно должен быть 0. Он и будет там, где функция ни возрастает, ни убывает – в точке вершины.
То же самое справедливо и для впадины (область, где функция слева убывает, а справа – возрастает):

Немного подробнее о приращениях.
Итак, мы меняем аргумент на величину Δx. Меняем от какого значения? Каким он (аргумент) теперь стал? Можем выбрать любую точку, и сейчас будем от нее плясать.
Рассмотрим точку с координатой x0. Значение функции в ней равно f(x0).
Затем делаем то самое приращение: увеличиваем координату x0 на Δx.
Чему теперь равен аргумент?
Очень легко: x0+Δx.
А чему теперь равно значение функции?
Куда аргумент, туда и функция: f(x0+Δx).
А что с приращением функции?
Ничего нового: это по-прежнему величина, на которую изменилась функция:
Δf = f(x0+Δx) − f(x0).
Потренируемся находить приращения:
|
|
|
1. Найди приращение функции f(x) = 2x + 3 в точке x0 = 2 при приращении аргумента, равном Δx.
2. Найди приращение функции y ( x ) = x 2 + 2x − 1 в точке x0 = 1 при приращении аргумента на Δx.
Решения:
- Приращение функции равно Δf=f(x0+Δx)−f(x0)
1) Найдём f(x0+Δx) = 2(x0+Δx)+3 (вместо х подставляем х0+ Δx)
2) Найдём f(x0) = 2x0 + 3 (вместо х подставляем х0)
3) Находим Δf
Δf = f(x0+Δx)−f(x0) =2(x0+Δx) − (2x0+3) = 2x0 + 2Δx + 3− 2x0 – 3 = 2Δx
Ответ: приращение функции равно Δf =2Δx
- Приращение функции равно Δу =у(x0+Δx)−у(x0)
1) Найдём у(x0+Δx), для этого в формулу y ( x ) = x 2 + 2x − 1 вместо х подставляем х0+ Δx. Получаем
у(x0+Δx) = (х0+ Δx)2 + 2(х0+ Δx)− 1 = х02+2х0 Δx+ Δx2+2х0+2 Δx − 1
2) Найдём у(x0), для этого в формулу y ( x ) = x 2 + 2x − 1 вместо х подставляем х0 . Получаем у(x0) = x0 2 + 2x0 – 1
3) Находим Δу =у(x0+Δx)−у(x0)
4) Δу= х02+2х0 Δx+ Δx2+2х0+2 Δx − 1 –( x0 2 + 2x0 – 1 ) = х02+2х0 Δx+ Δx2+2х0+2 Δx – 1 – x0 2 – 2x0 + 1= 2х0 Δx +Δx2+2 Δx=Δx(2х0+Δx +2)
В разных точках x0 при одном и том же приращении аргумента приращение функции будет разным. Значит, и производная в каждой точке своя (это мы обсуждали в самом начале – крутизна дороги в разных точках разная). Поэтому когда находим производную, надо указывать, в какой точке (х0):
|
|
|
f ′(х0) 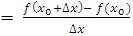 при при 
|
Дата добавления: 2020-04-25; просмотров: 70; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
