Метод интегрирования по частям.
Интегрирование по частям. Пусть  и
и 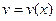 - дифференцируемые функции, тогда
- дифференцируемые функции, тогда 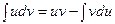 .Пример. Вычислить
.Пример. Вычислить 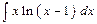 .
.
Пусть 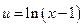 ,
, 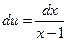 ,
, 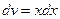 ,
, 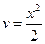 , тогда
, тогда 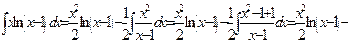
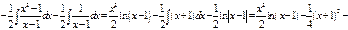
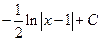 .
.
Разложение действительного многочлена на множители.
Теорема. Если 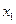 и
и 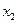 - корни квадратного уравнения, то справедливо следующее разложение
- корни квадратного уравнения, то справедливо следующее разложение 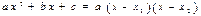 .
.
Пример. Разложить квадратный трехчлен 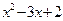 на множители. По теореме Виета определим корни квадратного трехчлена:
на множители. По теореме Виета определим корни квадратного трехчлена: 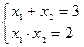 , откуда
, откуда 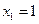 ,
, 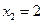 . Итак,
. Итак, 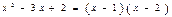 .
.
Разложить многочлен на множители означает представить его в виде произведения многочленов. Для этого используют различные приемы. Рассмотрим некоторые из них.
1.Вынесение общего множителя за скобку:
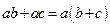 .
.
2. Группировка слагаемых:
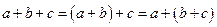 .
.
3. Формулы сокращенного умножения: 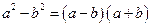 ,
, 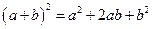 ,
, 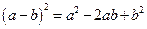 ;
; 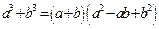 ,
, 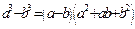 ;
; 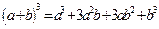 ,
, 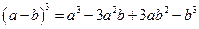 .
.
Теорема. Пусть дан многочлен 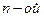 степени,
степени, 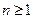 ,
, 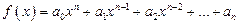 . Разложение
. Разложение 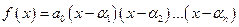 является для многочлена
является для многочлена 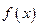 единственным с точностью до порядка сомножителей.
единственным с точностью до порядка сомножителей.
Разложение рациональной функции на простейшие дроби.
Когда степень многочлена знаменателя дроби равна нулю (т.е. в знаменателе стоит число), дробь является многочленом. По теореме известно, что любой многочлен может быть разложен на множители.
Если степень знаменателя дроби больше нуля и степень числителя меньше степени знаменателя, то дробь можно представить в виде простейших дробей. Если степень числителя больше дроби знаменателя, то необходимо выполнить деление многочлена на многочлен «углом».
Пример. Разложить рациональную функцию 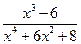 на простейшие дроби.
на простейшие дроби.
|
|
|
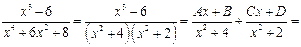
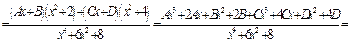
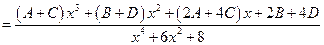 .
.
Определим 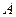 ,
, 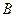 ,
, 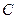 и
и 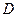 из системы уравнений
из системы уравнений 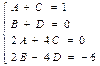 ,
, 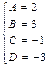 . Итак,
. Итак, 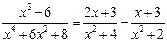 .
.
Интегрирование рациональных функций.
Интегрирование рациональных функций сводится к разложению дроби на простейший и проинтегрировав каждое слагаемое.
Пример. 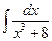 .
.
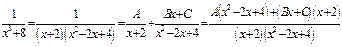
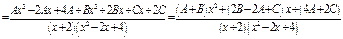 .
.
Определим 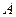 ,
, 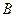 , и
, и 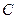 из системы уравнений
из системы уравнений 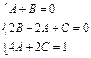 ,
, 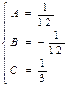 . Итак,
. Итак, 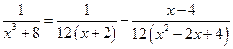 .
.
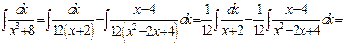
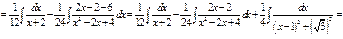
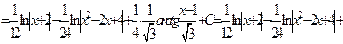
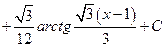 .
.
Интегрирование простейших иррациональностей.
Рассмотрим случаи, в которых замена переменной позволяет интегралы от иррациональных функций свести к интегралам от рациональных функций.
Обозначим через 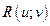 функцию от переменных
функцию от переменных 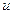 и
и 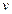 , и некоторых постоянных, которая построена с использованием лишь четырех арифметических действий (сложения, вычитания, умножения и деления). Например,
, и некоторых постоянных, которая построена с использованием лишь четырех арифметических действий (сложения, вычитания, умножения и деления). Например, 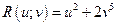 ,
, 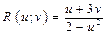 и т.д.
и т.д.
Рассмотрим интеграл вида 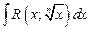 . Такие интегралы рационализируются заменой переменной
. Такие интегралы рационализируются заменой переменной 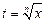 .
.
Пример. Вычислить 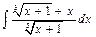 .
.
Пусть 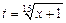 ,
, 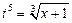 ,
, 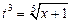 ,
, 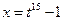 ,
, 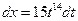 , тогда
, тогда 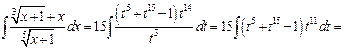

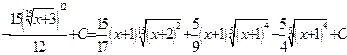 .
.
Биномиальный интеграл.
Биномиальным дифференциалом наз-ся выражение 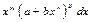 , где
, где 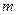 ,
, 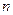 и
и 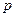 - рациональные числа.
- рациональные числа.
Интеграл от биномиального дифференциала 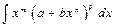 приводится к интегралу от рациональной функции в следующих трех случаях.
приводится к интегралу от рациональной функции в следующих трех случаях.
Случай 1. Показатель степени 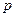 - целое число. Тогда интеграл
- целое число. Тогда интеграл 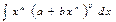 сводится к интегралу от рациональной функции с помощью подстановки
сводится к интегралу от рациональной функции с помощью подстановки 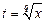 , где
, где 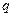 - общий знаменатель дробей
- общий знаменатель дробей 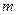 и
и 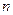 .
.
|
|
|
Случай 2. Число 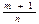 - целое. Тогда сводится к интегралу от рац.функции с помощью подстан.
- целое. Тогда сводится к интегралу от рац.функции с помощью подстан. 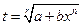 ,
, 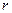 - знаменатель дроби
- знаменатель дроби 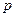 .
.
Случай 3. Число 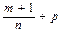 - целое. Тогда интеграл
- целое. Тогда интеграл 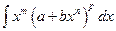 рационализируется с помощью подстановки
рационализируется с помощью подстановки 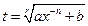 , где
, где 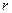 - знаменатель дроби
- знаменатель дроби 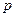 .
.
Пример. Найти интеграл 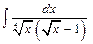 .
.
Здесь 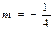 ,
, 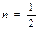 ,
, 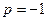 - целое число, т.е. имеет место первый случай интегрируемости. Поэтому следует применить подстановку
- целое число, т.е. имеет место первый случай интегрируемости. Поэтому следует применить подстановку 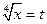 , тогда
, тогда 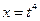 ,
, 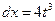 и данный интеграл принимает вид
и данный интеграл принимает вид 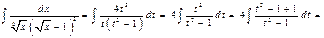
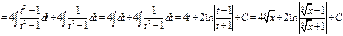
32 . Интегрирование функции 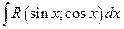 .
.
Рассмотрим интегралы вида 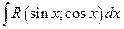 . Такие интегралы могут быть сведены к интегралам от рациональных функций заменой переменной
. Такие интегралы могут быть сведены к интегралам от рациональных функций заменой переменной 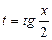 , где
, где 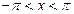 . Действительно
. Действительно 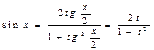 ,
, 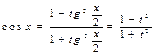 ,
, 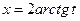 ,
, 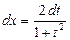 .
.
Пример. Вычислить 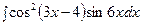 .
.
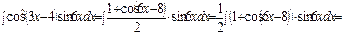
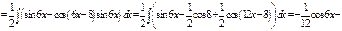
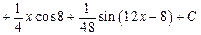 .
.
33 . Интегрирование функции 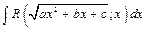 ,
, 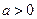 (первая подстановка Эйлера).
(первая подстановка Эйлера).
Интеграл вида 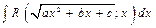 , где
, где 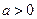 рационализируется с помощью первой подстановки Эйлера
рационализируется с помощью первой подстановки Эйлера 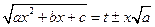 .
.
Пример. Найти интеграл 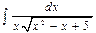 .
.
Здесь 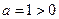 , поэтому применим подстановку
, поэтому применим подстановку  . Возведем обе части равенства в квадрат
. Возведем обе части равенства в квадрат 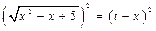 ,
, 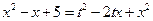 , приведем подобные члены, получим
, приведем подобные члены, получим 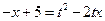 , откуда
, откуда 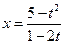 ,
, 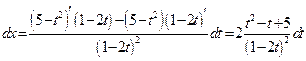 .
.
Подставляя полученные выражения в данный интеграл, имеем 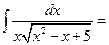
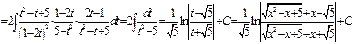
34 . Интегрирование функции 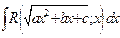 ,
, 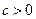 (вторая подстановка Эйлера).
(вторая подстановка Эйлера).
Интеграл вида 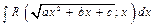 , где
, где 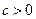 рационализируется с помощью первой подстановки Эйлера
рационализируется с помощью первой подстановки Эйлера 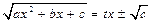 .
.
|
|
|
Пример. Найти интеграл 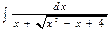 .
.
Здесь 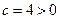 , поэтому применим подстановку
, поэтому применим подстановку 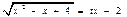 . Возведем обе части равенства в квадрат
. Возведем обе части равенства в квадрат 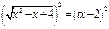 ,
, 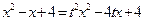 , приведем подобные члены, получим
, приведем подобные члены, получим 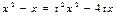 , откуда
, откуда 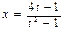 ,
, 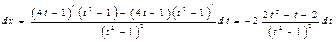 ,
, 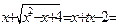
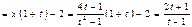 .
.
Подставляя полученные выражения в данный интеграл, имеем 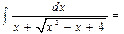
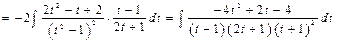 Разложим подынтегральную функцию на сумму простейших дробей:
Разложим подынтегральную функцию на сумму простейших дробей: 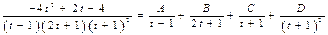 , откуда
, откуда 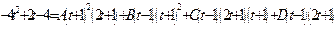 Полагая
Полагая 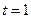 , находим
, находим 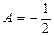 , при
, при 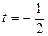 , получим
, получим 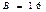 , при
, при 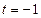 имеем
имеем 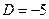 , тогда
, тогда 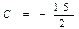 .
.
Таким образом, получаем 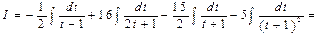
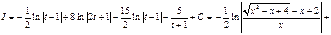
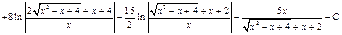
35 . Интегрирование функции 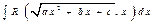 ,
, 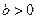 (третья подст.Эйлера).
(третья подст.Эйлера).
Интеграл вида 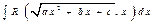 , где
, где 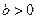 рационализируется с помощью первой подстановки Эйлера
рационализируется с помощью первой подстановки Эйлера 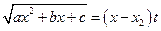 .
.
Пример. Вычислить 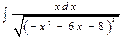 .
.
Здесь 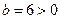 , поэтому применим подстановку
, поэтому применим подстановку 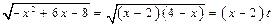 . Возведем обе части равенства в квадрат
. Возведем обе части равенства в квадрат 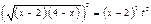 ,
, 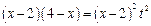 , откуда
, откуда  ,
, 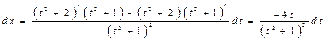 ,
, 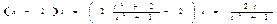 .
.
Подставляя полученные выражения в интеграл, 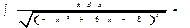
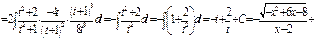
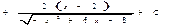 .
.
Дата добавления: 2020-04-25; просмотров: 106; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
